Цели: систематизировать, обобщать знания
учащихся, проверить уровень знаний по теме.
Развивать целеустремленность в достижении
поставленной задачи, честность в оценке своих
знаний и знаний товарищей, умения объяснять и
доступно рассказывать подготовленный материал.
Воспитывать познавательную активность,
культуру общения.
Цитата занятия:
"Пока законы математики
остаются определенными, они не имеют ничего
общего с реальностью;
как только у них появляется
нечто общее с реальностью, они перестают быть
определенными”.
Альберт Эйнштейн.
Ход занятия
1. Орг. момент. Проверить готовность учащихся
к занятию.
2. Теоретическая часть вопроса. Материал
подготовил и отвечал ученик.
Я хотел бы напомнить общие сведения о понятии
области определения функции.
– Рассмотрим числовое множество Х и
правило f, позволяющее поставить в
соответствие каждому элементу х на множестве
Х определенное число у, то говорят, что
задана функция у = f(x) с областью определения Х.
Пишут
у = f(x), х є Х.
Областью определения функции, заданной
некоторым выражением, называется множество
значений аргумента, при которых можно выполнить
все действия в записи функции. Значения
аргумента, принадлежащие области определения
функции, называются допустимыми значениями.
Для области определения функции используют
обозначение D(y).
Если f(x) – алгебраическое выражение и
область определения функции у = f(x) совпадает
с областью определения этого выражения (такую
область определения называют естественной), то
вместо записи у = f(x), х є Х используют более короткую
запись: у = f(x).
Для нахождения области определения функции
следует исключить те значения аргумента, при
которых указанные действия невозможно
выполнить. Невозможно, например, делить на нуль;
извлекать корень четной степени из
отрицательного числа; вычислять логарифм
отрицательного числа и нуля; вычислять логарифм
по отрицательному основанию и основанию, равному
нулю и единице; возводить нуль в степень нуля;
возводить отрицательное число в иррациональную
степень; вычислять arcsin x, arсcos x, если |x|>1.
3. Рассмотрение вопроса на примерах. Материал
подготовил и рассказывал ученик.
Я хотел бы рассмотреть некоторые важные
моменты при нахождении области определения:
1) знаменатель дробного выражения не должен
обращаться в нуль. Например: у = 1/х,
область определения состоит из всех х 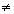 0; 0;
у = sin x/cos x, область определения
состоит из всех х, для которых cos x не = 0, т.е. из (n = 0, 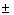 1, 1, 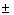 2, …): 2, …):
2) выражение, находящееся под знаком корня
четной степени, должно быть неотрицательным.
Например: у = 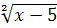 , область определения , область определения
у = 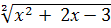
3) выражение, находящееся под знаком логарифма
должно быть положительным. Например: у = lg(2-х),
область определения 2-х >0, т.е. х < 2.
4) основание логарифма должно быть больше нуля и
не равным единице. Например: у = logх+27,
область определения х + 2 > 0 и х + 2 не = 1, т.е. х > -2 и х не= – 1;
5) выражение, возводимое в иррациональную
степень, должно быть неотрицательным.
6) выражение стоящее под знаком функций arcsin и
arсcos, по абсолютной величине не должно быть
больше единицы. Например: у = arcsin(lg х),
область определения |lg x| =< 1 т.е. 0,1 =< х =< 10;
7)степенно-показательная функция считается
определенной, когда основание положительно.
Точки, в которых основание равно нулю, включаются
в область определения, если показатель в этих
точках отличен от нуля.
Этот вопрос я подготовил пользуясь пособием по
математике (авторы: М.Н.Горейко, А.Б. Антоневич)
4. Примеры нахождения D(y). Материал
подготовил и рассмотрел перед классом ученик.
Найти области определения функций:
- у =
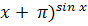 . . Решение. Так как sin x принимает и
иррациональные значения, то x + п>= 0, т.е. х >=-п. Кроме того, х не
должен обращаться в -п, так как при х = -п и основание, и показатель
степени обращаются в нуль. Область определения
функции у = 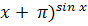 есть х > -п.
есть х > -п.
- у =
 . . Решение. Области определения этой функции
принадлежат те х, при которых 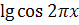 определен и определен и 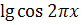 >= 0. Для этого
нужно, чтобы >= 0. Для этого
нужно, чтобы 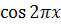 >= 1.
Но последнее неравенство справедливо лишь в
точках х = 0, +-1, +-2, … . Таким образом,
только в этих точках можно выполнить все
действия в записи функции и, значит, область
определения этой функции состоит только из целых
чисел. >= 1.
Но последнее неравенство справедливо лишь в
точках х = 0, +-1, +-2, … . Таким образом,
только в этих точках можно выполнить все
действия в записи функции и, значит, область
определения этой функции состоит только из целых
чисел. - у = logх – 1(х2 + х – 2).
Решение. Логарифм определен только для
положительных оснований, не равных единице.
Выражение, стоящее под знаком логарифма, должно быть положительным. Поэтому получаем систему:
х -1 > 0;
х2 – х – 2 > 0;
х – 1 не = 1.
Решая эту систему, находим область определения:
х > 1, х не = 2.
5. Метод Мажорант (метод оценки). Решение
уравнений.
Материал рассмотрен учителем вместе с
учениками.
Метод, который имел место быть во всех ЕГЭ по
математике. Отметим этот метод, как начальный
олимпиадный.
Основная идея метода мажорант состоит в
следующем:
Пусть мы имеем уравнение 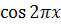 и существует такое число М,
что для любого х из области определения и существует такое число М,
что для любого х из области определения 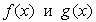 имеем имеем 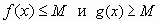 . Тогда уравнение . Тогда уравнение 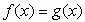 равносильно
системе равносильно
системе 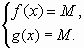 | 
