Цели:
- повторить методы решения уравнений с
переменной под знаком модуля;
- закрепить навыки и умения решения уравнений с
переменной под знаком модуля;
- дать возможность каждому ученику
самореализоваться, раскрыть свои способности и
возможности.
Тип урока: обобщение.
Оборудование: компьютер, мультимедийный
проектор, экран; лист контроля "Путь к успеху”
для каждого учащегося.
Ход занятия
I. Оргмомент.
(Сообщение темы и цели занятия.
Открывается слайд)
Правила заполнения листа "Путь к успеху”.
В течение всего занятия, по каждому этапу
ребята заполняют листы в следующем порядке.
1 этап.
Это задание выполняется сразу на листках.
В колонке "ответ” в таблицу записываются
номера уравнений.
2 этап.
Запишите только задание и ответ в
соответствующие колонки.
3 этап.
В колонке "задание” коротко запишите свое
решение и соответственно ответ.
4 этап.
Записывается задание и ответ.
II. Актуализация знаний.
Водная беседа по вопросам.
- Дайте определение абсолютной величины.
- Назовите группы методов решения уравнений,
которые мы с вами изучили?
Ответ:
- Поясните в чем суть этого метода?
2 - метод равносильного перехода к
совокупностям двух смешанных систем.
- Поясните.
Этот метод позволяет освободиться от
абсолютной величины при непосредственном
использовании ее определения.
Его реализацию наглядно демонстрирует
следующее очевидное утверждение.
Уравнение вида
| f(x) | = q(x)
равносильно совокупности двух смешанных
систем
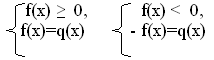
- метод равносильного перехода к системе,
состоящей из неравенства и совокупности двух
уравнений.
- Поясните суть этого метода.
Уравнение вида
| f(x) | = q(x)
реализуется на основе того, что все корни
уравнения содержатся среди корней уравнений
f(x)=q(x) , f(x)= -q(x) и удовлетворяют условию q(x)>= 0.
Необходимые записи по ходу выполняются на
доске.
III. Выполнение заданий.
1 этап
"Входной контроль”
- Распределите следующие уравнения по методам
их решения в таблицу. (При выполнении этого
задания на листах, уравнения записывать не надо,
достаточно указать только номер)
(Открывается слайд "Таблица”)
| Метод промежутков |
Метод равносильного перехода к
совокупностям двух смешанных систем |
Метод равносильного перехода к системе,
состоящей из неравенства и совокупности двух
уравнений |
| |
|
|
(Открывается слайд с уравнениями)
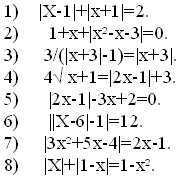
(После проделанной работы, заслушать ответы
нескольких учащихся с объяснением) "Проверь себя”
Заранее учитель формирует группы по
способностям. Первая группа - недостаточного
уровня, вторая- среднего уровня и третья высокого
уровня. (На следующий урок можно поменять
разноуровневые группы)
1 ряд – решает уравнение на выбор из первой
группы методов.
2 ряд - решает уравнение на выбор из второй
группы методов.
3 ряд - решает уравнение на выбор из третьей
группы методов. "Защита решения”
(2 ученика на доске, желательно из второй и
третьей группы, воспроизводят решение на доске,
т.е. защищают свое решение). В это время остальные
учащиеся записывают коротко свое решение на
листах контроля. "Умники и умницы”
Это задание выполнять в парах. Каждая пара
выбирает себе дорожку.
Красная дорожка – решить одно уравнение.
Желтая дорожка – решить два уравнения.
Зеленая дорожка – решить три уравнения.
Каждая дорожка имеет свой уровень сложности, но
задача учеников как можно быстрее справиться с
выбранными заданиями, отметить в листах контроля
выбранную дорожку и записать ответ.
(Открывается слайд на проекторе с заданием)

Учитель:
- Ребята, проверьте свои решения (открывается
очередной слайд с ответами).

IV. Рефлексия.
-Какие группы методов для решения уравнений вы
сегодня использовали?
-Можно ли при решении уравнений сложной
структуры сочетать различные методы?
Например, проанализируем решения уравнения с
красной дорожки (используется дважды метод №3
или № 3 и №2).
V. Домашнее задание.
Решить оставшиеся уравнения из таблицы,
рассмотренные в начале урока. | 
