Тип урока: обобщающий урок.
Цели урока:
- обобщить и проконтролировать знания и умения
учащихся по теме "Параллельность прямых и
плоскостей”;
- развивать интерес к предмету, навыки применения
теоретических знаний при выполнении упражнений,
способствовать развитию логического мышления;
- воспитывать трудолюбие, упорство,
целеустремлённость, любовь к творчеству, чувство
коллективизма, уважительное отношение к мнению
партнёра.
Форма проведения – игра КВН
Подготовительный этап: класс разбивается на
две команды, каждая получает домашнее задание:
составить и оформить кроссворд, изготовить
модели тетраэдра и параллелепипеда.
План урока (сдвоенный урок):
- Конкурс "приветствие”.
- Конкурс "разминка”.
- Конкурс капитанов.
- Конкурс болельщиков.
- Конкурс "умников” (решение задач).
Ход игры
I. Организационный момент.
Участники и гости занимают места.
– Здравствуйте, дорогие гости, болельщики и
участники нашей встречи. Сегодня у нас состоится
зачёт по геометрии по теме "Параллельность
прямых и плоскостей”, который мы проведём в
несколько необычной форме – в форме игры КВН.
Цель участников команд и их болельщиков –
показать все знания и умения по изученным темам.
А оценивать ваши знания будут почётные гости –
члены жюри во главе с председателем
...(представление председателя и членов жюри).
Итак, сегодня соревнуются две команды:
"Тетраэдр” и "Параллелепипед”. И прежде чем мы
начнём нашу игру, мне хотелось бы
поприветствовать участников и пожелать им удачи.
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
Мы в поход отправляемся смело
В мир загадок и сложных задач.
Не беда, что идти далеко.
Не боимся, что путь будет труден.
Достижения крупные людям
Никогда не давались легко. (Н.К.Антонович)
I конкурс "Приветствие”.
Учитель
Представители каждой команды рассказывают о
многограннике, именем которого назвались,
комментируя свой рассказ по изготовленному
заранее макету тетраэдра (параллелепипеда). Тем
временем представители команды соперников
решают задачу на построение сечения.
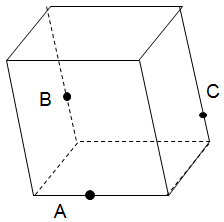
Задача команде "Тетраэдр”: построить сечение
параллелепипеда плоскостью АВС. <Рисунок 1>
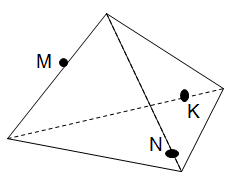
Задача команде "Параллелепипед”: построить
сечение тетраэдра плоскостью MNK. <Рисунок 2>
II конкурс "Разминка”
Учитель
Команды приготовили друг для друга кроссворды,
которые соперники должны сейчас разгадать.
Первыми свой кроссворд представят
"Параллелепипеды”. Потом меняются ролями.
III конкурс "Конкурс капитанов”
Учитель
На карточках написаны названия теорем (признак
параллельности прямой и плоскости, признак
скрещивающихся прямых, признак параллельности
двух плоскостей, лемма о пересечении плоскости
параллельными прямыми, теорема об углах с
сонаправленными сторонами). Капитаны по очереди
тянут карточку и доказывают попавшуюся теорему
на доске. Тем временем участники команд
разбиваются на два варианта и на листках
доказывают теоремы: 1 вариант – о параллельности
трёх прямых
2 вариант – второе следствие из аксиом.
А болельщикам в это время предлагается
поддержать команды, ответив на вопросы и верными
ответами заработать дополнительные баллы для
своей команды.
Вопросы болельщикам команды "Тетраэдр”.
- Сформулируйте первую аксиому стереометрии.
- Сформулируйте вторую аксиому стереометрии.
- Как звучит первое следствие из аксиом?
- Продолжите высказывание "если одна из
параллельных прямых пересекает плоскость...”.
- Дайте определение скрещивающихся прямых.
- Сформулируйте теорему об углах с
сонаправленными сторонами.
- Плоскости называются параллельными, если...
- Отрезки параллельных прямых...(закончите фразу).
- Дайте определение многогранника.
- Что называют параллелепипедом?
- Диагонали параллелепипеда...(свойство).
- Какие грани параллелепипеда называются
противоположными?
- Диагональю параллелепипеда называется...
- Какую плоскость называют секущей плоскостью
многогранника?
- Какой многоугольник может быть сечением
параллелепипеда?
Вопросы болельщикам команды
"Параллелепипед”.
- Сформулируйте третью аксиому стереометрии.
- Как звучит второе следствие из аксиом?
- Какие прямые в пространстве называются
параллельными?
- Каким может быть взаимное расположение прямой и
плоскости в пространстве?
- Продолжите: "через каждую из скрещивающихся
прямых...”.
- Сонаправленными называются лучи...
- Если две параллельные плоскости пересечены
третьей...
- Дайте определение многоугольника.
- Тетраэдр – это...
- Противоположными называются грани
параллелепипеда...
- Какие рёбра тетраэдра называются
противоположными?
- Какие вершины параллелепипеда называются
противоположными?
- Какие грани параллелепипеда называются
смежными?
- Что называют сечением многогранника?
- Какой многоугольник может быть сечением
тетраэдра?
Далее участники сдают листочки с
доказательствами теорем на проверку капитану
соперников, предварительно заслушав ответы
самих капитанов. Те, проверив работы,
подсчитывают средний балл и передают результат
членам жюри.
IV конкурс "Решение задач”.
Учитель
Проведя хорошую теоретическую подготовку,
можно приступать к самому сложному конкурсу. Вы
должны будете применить свои теоретические
знания при решении задач.
По одному представителю от команд решают
задачу на доске, ещё по три участника работают с
карточками на местах. Решив задачу, они находят
карточку с числом, соответствующим ответу
задачи, и по коду в углу этой карточки находят
бумажную полосу, на которой написана часть
высказывания. Решив верно все задачи, они сложат
записи и прикрепят их к доске.
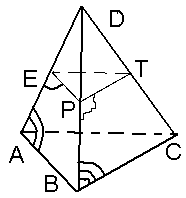
Задачи команде "Тетраэдр”.
№1.В тетраэдре DABC точки А1, В1 и С1–
середины рёбер DA, DB и DC соответственно.
а) докажите, что АВС ~ А1В1С1;
б) найдите площадь А1В1С1, если площадь АВС равна 44 см2.
№2 Концы двух пересекающихся отрезков АС и ВД
лежат на двух параллельных плоскостях, причём
расстояния между точками одной плоскости равны.
а) докажите, что АВ || СД.
б) один из углов четырёхугольника АВСД равен 65°.
Найдите остальные углы.
№3. Вершины В и С треугольника АВС лежат в
плоскости а, а
вершина А не лежит в этой плоскости. Прямая а
параллельна прямой АС и пересекает сторону АВ в
точке М так, что АМ:МВ=3:4.
а) докажите, что прямая а пересекает
плоскость 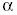 . .
б) найдите сторону АС, если длина отрезка прямой а
от точки М до плоскости 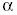 равна 7 см. равна 7 см.
№4. Треугольник АВС и квадрат AEFC не лежат в
одной плоскости. Точки К и М – середины отрезков
АВ и ВС соответственно.
а) докажите, что КМ || EF.
б) найдите КМ, если АЕ=8 см.
Задачи команде "Параллелепипед”.
№1. Отрезок АВ не пересекается с плоскостью 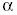 . Через концы
отрезка АВ и его середину М проведены
параллельные прямые, пересекающие плоскость . Через концы
отрезка АВ и его середину М проведены
параллельные прямые, пересекающие плоскость  в точках А1,
В1 и М1 соответственно. в точках А1,
В1 и М1 соответственно.
а) докажите, что точки А1, В1 и М1
лежат на одной прямой.
б) найдите АА1, если ВВ1=12см, ММ1=8см.
№2. Даны треугольник АОВ и параллелограмм АВСД,
не лежащие в одной плоскости.
а) определите взаимное расположение прямых АО и
СД (с доказательством)
б) найдите угол между прямыми АО и СД, если угол
ОАВ=130°.
№3 На сторонах АВ и АС треугольника АВС взяты
соответственно точки Р и Т, РТ=4см., АР:РВ=1:3.
Плоскость а
проходит через точки Р и Т и параллельна отрезку
ВС.
а) доказать, что отрезки РТ и ВС параллельны.
б) найдите отрезок ВС.
№4. В параллелепипеде АВСДА1В1С1Д1
диагонали равны. Найдите угол между диагональю
АС1 и диагональю боковой грани АВ1,
если АД+СВ=АС1.
Решив верно задачи, участники сложат
высказывания:
"Не всякому помогает случай; судьба одаряет
только подготовленные умы” (Л. Пастер).
"Не говори всегда, что знаешь, но знай всегда, что
говоришь” (Клавдий).
Тем временем, пока решаются эти задачи,
остальные участники команд решают устные задачи
по заготовленным чертежам. (Команды отвечают по
очереди).
Задачи команде "Тетраэдр”
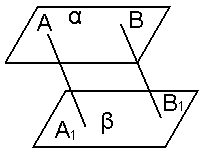
6. Дано: АА1 || ВВ1; АА1=ВВ1
Каково взаимное расположение плоскостей а и б? <Рисунок 5>
Задачи команде "Параллелепипед”.
- Через прямую а и точку А можно провести две
различные плоскости. Каково взаимное
расположение прямой а и точки А? (Ответ
объясните).
- Прямая КМ пересекает стороны АВ и АС
треугольника АВС. Каково взаимное расположение
прямой КМ и плоскости АВС? Ответ обоснуйте.
- Прямые а и в параллельны. Докажите, что
все прямые, пересекающие данные, лежат в одной
плоскости.
- Даны две параллельные плоскости а и б. В плоскости алежит прямая а, а в плоскости б – прямая в.
Каковы возможные случаи взаимного расположения
прямых а и в?
- Одна из сторон треугольника АВС принадлежит
плоскости а.
Плоскость б
параллельна плоскости а и пересекает другие стороны
треугольника в точках М и К.
Доказать, что б отсекает от треугольника треугольник,
подобный данному. <Рисунок 6> 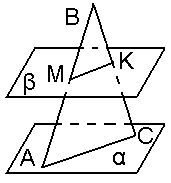
- Дано: а || б, АА1 || ВВ1
АВ=10 см.
Найти А1В1. <Рисунок 7>
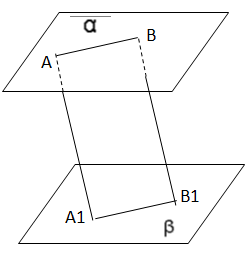
V. Подведение итогов.
| 
