Чтобы найти наименьшее общее кратное натуральных чисел 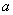 и и 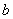 надо: надо:
- разложить их на простые множители;
- выписать множители, входящие в разложение одного их чисел;
- добавить к ним недостающие множители из разложений остальных чисел;
- найти произведение получившихся множителей.
- Указать среди данных произведений разложение числа 700 на простые множители:
а) 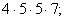
б) 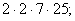
в) 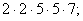
г) 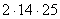 - Если вы верно выполнили задание, то получили ответ в; если
получили другой ответ, то повторите определение простых и составных
чисел.
- Прочитайте определение наименьшего общего кратного натуральных чисел: Наименьшим общим кратным натуральных чисел
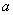 и и 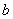 называется наименьшее натуральное число, которое кратно и называется наименьшее натуральное число, которое кратно и 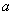 , и , и 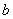 . . - Разложить на простые множители числа 15 и 35.
- Выписать множители, входящие в разложение числа 15.
- Выписать множители, входящие в разложение числа 35.
- Прочитайте алгоритм нахождения наименьшего общего кратного натуральных чисел и выполните п.2 и п.3 из него для чисел 15 и 35.
- Найдите произведение множителей
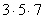 . Полученное произведение и будет наименьшим общим кратным чисел 15 и 35. Обозначение НОК(15;35) . Полученное произведение и будет наименьшим общим кратным чисел 15 и 35. Обозначение НОК(15;35) - Прочитайте алгоритм нахождения наименьшего общего кратного
натуральных чисел и найдите наименьшее общее кратное чисел 4, 6, 15.
- Найдите наименьшее общее кратное чисел 6, 9, 12.
- Какие числа называются взаимно простыми?
- Являются ли числа 54 и 65 взаимно простыми?
- Приведите 2-3 примера взаимно простых чисел.
- Прочитайте алгоритм нахождения наименьшего общего кратного натуральных чисел и найдите наименьшее общее кратное чисел:
а) 2 и 3;
б) 5, 8 и 3.
Вывод: Наименьшее общее кратное взаимно простых чисел равно произведению этих чисел.
| 
