Когда на окраине городка открывается ярмарка, всех от мала до велика охватывает радостное возбуждение (говоря о всех, я имею в виду «всех, кроме коров»).

В этом году в одном из павильонов ярмарки желающие могли сыграть в новую игру, которая так и называется — «игра в 15».

Мистер Ярмар. Рад приветствовать вас! Добро пожаловать к нам! Правила игры в 15 очень просты. Мы с вами по очереди ставим по монете на эти числа от 1 до 9. Кто ходит первым, безразлично.

Мистер Ярмар. Вы отмечаете свои ходы центами, я отмечаю свои ходы серебряными долларами. Выигрывает тот, кто первым накроет своими монетами 3 числа, дающие в сумме 15. Выигравший забирает все монеты, выложенные на стол.

Посмотрим, как играют в 15. Первый ход — дама ставит цент на 7. Поскольку цифра 7 накрыта, ставить на нее в дальнейшем нельзя; ни доллары, ни центы. То же можно сказать и обо всех остальных цифрах: ни одну из них нельзя накрывать монетами дважды, будь то центы или доллары.

Мистер Ярмар ставит доллар на 8.

Дама делает второй ход и ставит цент на 2. Если ей удастся поставить цент на 6, она выиграет.

Мистер Ярмар, желая воспрепятствовать выигрышу партнера, ставит доллар на 6. Он выиграет, если ему удастся поставить доллар на 1.

Дама замечает угрозу и блокирует мистеру Ярмару путь к выигрышу, ставя цент на 1.

Мистер Ярмар с усмешкой ставит доллар на 4. Дама замечает, что если он следующим ходом поставит доллар на 5, то выиграет, и отрезает ему этот путь к выигрышу.

Дама ставит цент на 5.

Но мистер Ярмар ставит доллар на 3 и выигрывает, так как 8 + 4 + 3 = 15. Дама проиграла свои 4 цента.

Мэру города игра в 15 очень понравилась. Пронаблюдав за игрой в течение почти целого дня, он пришел к убеждению, что мистер Ярмар придерживается тайной беспроигрышной стратегии.

Всю ночь напролет мэр пытался разгадать, в чем состоит тайная стратегия мистера Ярмара.

Внезапно мэра озарила поразительная по простоте идея.

Мэр. Я так и знал, что должна быть какая-то система! У доверчивых простаков, надеющихся заполучить серебряные доллары мистера Ярмара, нет ни шанса на выигрыш.

Какая идея осенила мэра? Не могли бы вы самостоятельно разработать беспроигрышную стратегию для игры в 15?

Старые добрые «крестики-нолики»!

Выигрышную стратегию указать нетрудно, если догадаться, что игра в 15 мистера Ярмара математически эквивалентна игре в «крестики-нолики». Установить эквивалентность нам поможет ло-шу — магический квадрат 3×3, впервые открытый в древнем Китае.

Чтобы в полной мере оценить изящество этого магического квадрата, выпишем прежде всего все возможные тройки однозначных чисел (попарно не равных и отличных от нуля), которые в сумме дают 15. Существует 8 таких троек:

1 + 5 + 9 = 15,

1 + 6 + 8 = 15,

2 + 4 + 9 = 15,

2 + 5 + 8 = 15,

2 + 6 + 7 = 15,

3 + 4 + 8 = 15,

3 + 5 + 7 = 15,

4 + 5 + 6 = 15.

Теперь присмотримся повнимательнее к единственному магическому квадрату 3×3:

2 9 4

7 5 3

6 1 8

Если считать, что каждое число вписано в единичный квадрат (составляющий 1/9 от квадрата 3×3), то можно выделить 8 троек единичных квадратов, лежащих: на одной прямой: 3 горизонтали, 3 вертикали и 2 диагонали. Каждая из прямых соответствует одной из троек чисел, дающих в сумме 15. Следовательно, любой набор из 3 чисел, обеспечивающий победу в игре мистера Ярмара, соответствует либо горизонтали, либо вертикали, либо диагонали магического квадрата.

Нетрудно видеть, что любая партия в 15 эквивалентна партии а «крестики-нолики», разыгрываемой на магическом квадрате. У мистера Ярмара имеется магический квадрат, начерченный на листке бумаги, в который он тайком поглядывает. Хотя существует единственный квадрат ло-шу, но его можно повернуть четырьмя разными способами и, если угодно, подвергнуть зеркальному отражению. Любая из 8 разновидностей магического квадрата может служить тайным ключом к гроссмейстерской стратегии при игре в 15.

Играя с посетителем павильона в 15, мистер Ярмар мысленно играет с ним в «крестики-нолики» на магическом квадрате. Если игра в «крестики-нолики» происходит по всем правилам, то партия в 15 кончается вничью. Но легковерные посетители павильона, вздумавшие сразиться с мистером Ярмаром в 15, лишены огромного преимущества, так как не сознают, что в действительности играют в «крестики-нолики». Это облегчает задачу мистеру Ярмару, и он подстраивает своим партнерам каверзы и ловушки, вынуждая их делать ходы, ведущие к его выигрышу.

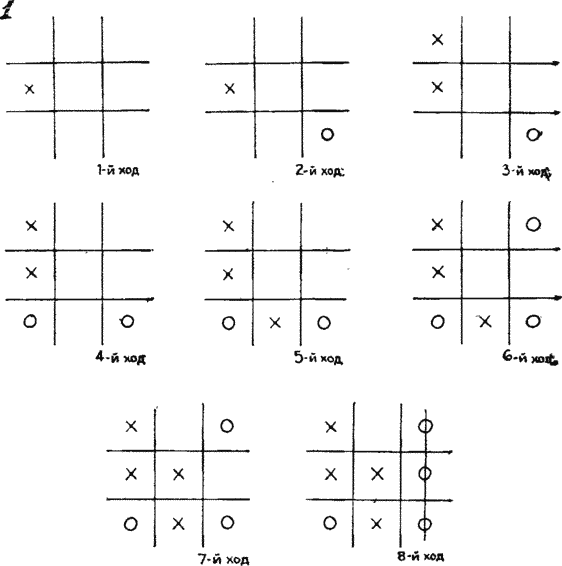
Чтобы разобраться, как действует мистер Ярмар, рассмотрим подробно партию, изображенную на картинках. Ходы приведены на диаграммах, показанных на рис. 1. Даже если мистер Ярмар ходит вторым (ставит нолики), то на шестом ходу он может поставить даме западню, которая обеспечит ему выигрыш на восьмом ходу независимо от того, как именно пойдет дама на седьмом ходу. Всякий, кто умеет играть на гроссмейстерском уровне в «крестики-нолики», взяв на вооружение магический квадрат, станет непобедимым игроком в 15.

Понятие изоморфизма (математической эквивалентности) — одно из важнейших в математике. Во многих случаях трудная задача легко решается, если ее удается свести к изоморфной уже решенной задаче. По мере того как математика разрастается вглубь и вширь, она становится все более единой, все более упрощается по мере открытия все новых и новых изоморфизмов. Например, найденное в 1976 г. решение знаменитой проблемы четырех красок позволило доказать десятки других важных гипотез в иных разделах математики, которые были изоморфны проблеме четырех красок.

Чтобы помочь вам глубже разобраться в сущности такого фундаментального понятия, как изоморфизм, рассмотрим следующую игру в слова, Берется 9 слов:

БУСЫ

ХЛЕБ

БАНЯ

ПЛУГ

СНЕГ

ГАТЬ

УРОН

ОРЕХ

МАРС

Двое игроков по очереди вычеркивают по одному слову, помечая каждый сделанный ход своими инициалами или условным значком. Выигрывает тот, кому первым удастся вычеркнуть три слова, имеющие общую букву. Пройдет немало времени, прежде чем игроки поймут, что и на этот раз они играют в добрые старые «крестики-нолики». Изоморфизм игр нетрудно установить, если вписать слова в клетки таблички, расчерченной для игры в «крестики-нолики» (рис. 2). Как нетрудно проверить, общая буква имеется лишь у трех слов, расположенных по горизонталям, вертикалям и диагоналям. Тем самым доказано, что играть в слова означает по существу играть в «крестики-нолики», и наоборот (или в 15).

Попробуйте подобрать другие 9 слов для игры. Разумеется, отнюдь не обязательно играть именно в слова родного языка. С тем же успехом можно воспользоваться и абстрактными символами, как это сделано на рис. 3.

Еще лучше играть во все эти игры, записав слова, знаки или цифры на 9 карточках. Разложив точки на столе исписанной стороной вверх, игроки могут по очереди брать по одной карточке до тех пор, пока одни из них не выиграет.

Разобравшись в изоморфизме игры в 15, «крестики-нолики» и игры в слова, приступим к новой игре — на дорожной сети. В нее играют на карте дорог, изображенной на рис. 4.

Между восемью городами проложены дороги. Вооружившись цветными карандашами (один игрок пусть выберет красный карандаш, а другой — синий), игроки по очереди закрашивают по одной дороге (каждую дорогу необходимо закрашивать целиком). Обратите внимание, что некоторые дороги проходят через города не обрываясь. В таких случаях закрашивать дорогу нужно не только до ближайшего города, а на всем ее протяжении. Выигрывает тот, кому первым удастся закрасить три дороги, ведущие в один и тот же город. На первый взгляд кажется, что новая игра не имеет ни малейшего отношения к трем уже рассмотренным нами играм. В действительности же и она изоморфна игре в «крестики-нолики»!

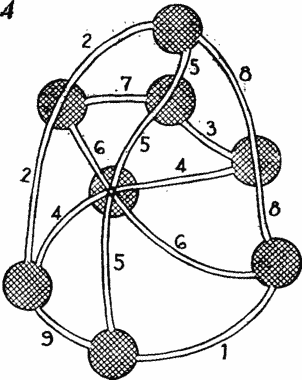
Чтобы установить изоморфизм, достаточно перенумеровать дороги так, как показано на рис. 4. Каждая дорога соответствует клетке магического квадрата, помеченной тем же числом. Каждый город на карте соответствует горизонтали, вертикали или диагонали в магическом квадрате. Как и в предыдущих случаях, изоморфизм полный. Всякий, кто умеет на гроссмейстерском уровне играть в «крестики-нолики», не будет знать горечи поражений и в новой игре.

На рис. 5 изображен один из 880 различных (не переходящих друг в друга под действием поворотов и отражений) магических квадратов 4×4. Постоянная этого квадрата (сумма чисел, стоящих на любой горизонтали, вертикали и диагонали) равна 34. Может ли такой квадрат служить ключом для беспроигрышной игры в 34, то есть игры, в которой игроки по очереди выбирают число от 1 до 16 (ни одно число не разрешается выбирать дважды) до тех пор, пока у одного из игроков не наберется четыре числа, дающие в сумме 34. Изоморфна ли игра в 34 игре в «крестики-нолики» на магическом квадрате, изображенном на рис. 5? Нет, не изоморфна! Почему?

Можно ли так изменить правила игры в «крестики-нолики», чтобы победную комбинацию образовывали четыре клетки, не лежащие на одной горизонтали, вертикали или диагонали, и утраченный изоморфизм был восстановлен?