Кухня в ресторане «У Джо» оставляет желать лучшего, зато выбор сыров у Джо отменный.

Цилиндрическая головка сыра таит в себе немало интересных задач на разрезание. Проведя лишь 1 прямолинейный разрез, ее нетрудно разделить на 2 одинаковые части.

Два прямолинейных разреза позволяют разделить головку сыра на 4 одинаковые части, а 3 прямолинейных разреза — на 6 равных частей.

Однажды официантка Рози попросила Джо разрезать сыр на 8 одинаковых частей.

Джо. Хорошо, Рози. Сделать это совсем нетрудно. Я разделю сыр на 8 одинаковых частей четырьмя прямолинейными разрезами.

Подавая сыр на стол, Рози вдруг поняла, что Джо мог действовать и более экономно: чтобы разделить головку на 8 одинаковых частей, достаточно провести лишь 3 прямолинейных разреза.

Как это сделать?

Три разреза?

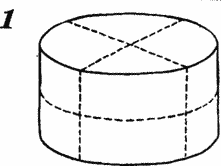
Рози пришло в голову, что цилиндрическая головка сыра представляет собой не плоскую фигуру, а тело, которое можно разрезать по горизонтальной плоскости, проходящей через его центр. На рис. 1 показано, как тремя разрезами разделить сыр на 8 одинаковых порций. В этом решении предполагается, что все три разреза проведены одновременно. Если же разрезы проводить последовательно, один за другим, и перед каждым разрезом переставлять куски сыра наиболее удобным образом, то тремя разрезами сыр можно разрезать по-другому (так, как он разрезан^на подносе в руках Рози): для этого один из двух кусков, получившихся после первого разреза, нужно поставить на другой, провести еще один разрез, взять одну из «двухэтажных» половин, поставить на другую и провести третий разрез. После третьего разреза головка сыра окажется разделенной на 8 одинаковых порций.

Решение Рози столь просто, что кажется почти травиальным, и тем не менее оно может служить хорошим введением в серию важных задач на разрезание, теория которых связана с исчислением конечных разностей, а многие доказательства проводятся методом математической индукции. Конечные разности служат мощным средством получения формул общих членов числовых последовательностей. Интерес к числовом последовательностям неуклонно возрастает, что объясняется по крайней мере двумя причинами: во-первых, тем, что числовые последовательности встречаются во многих числовых задачах, и, во-вторых, быстротой, с которой ЭВМ позволяют производить над числовыми последовательностями любые действия.

Изобретенный Рози первый метод разрезания сыра (без перекладывания кусков) состоит в проведении прямолинейных или, лучше сказать, плоских разрезу проходящих через центр верхнего основания готовки сыра, плоского, как у круглого пирога. Выясним, какие числовые последовательности может порождать разрезание верхней поверхности сыра прямыми, пересекающимися в центре (ясно, что n одновременно проведенных разрезов позволяют разделить сыр не более чем на 2n кусков).

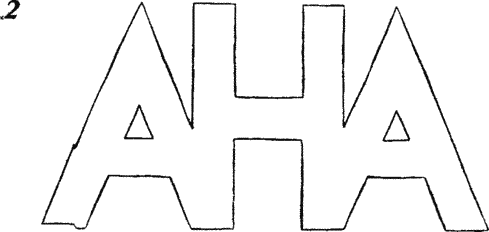
Можно ли считать, что 2n — максимальное число частей, на которые n прямых, проходящих через одну точку, могут разделить любую плоскую фигуру, ограниченную простой замкнутой кривой? Нет: нетрудно построить невыпуклую фигуру (например, такую, как на рис. 2), которую одной прямой можно разделить на значительно большее число частей. А можно ли построить фигуру, которую одной прямой можно было бы разделить на любое конечное число конгруэнтных частей? Если да, то какими свойствами должен обладать периметр фигуры, чтобы одной прямой от нее можно было отсечь п конгруэнтных частей?

Задача о разрезании пирога или сыра становится еще более интересной, когда линии разреза не пересекаются в одной точке. Нетрудно видеть, что начиная си = 3 при таком способе разрезания исходный круг будет распадаться более чем на 2n частей (пока нас не интересует, будут ли эти части конгруэнтными или равновеликими). На рис. 3 показано, каким образом достигается максимальное число частей при числе разрезов n, равном 1, 2, 3 и 4 (круг делится соответственно на 2, 4, 7 и 11 частей).

Числа 2, 4, 7 и 11 образуют отрезок известной последовательности с общим членом, задаваемым формулой

где n — число разрезов. Полагая п = 0, 1, 2, …, 9, получаем первые десять членов последовательности: 1, 2, 4, 7, 11, 16, 22, 29, 37, 46…. Первые разности равны 1, 2, 3, 4, 5, 6, 7, 8, 9, …, вторые разности равны 1, 1, 1, 1, 1, 1, 1, 1, … . Постоянство вторых разностей основательно подкрепляет нашу догадку о тем, что общий член этой последовательности квадратичен по n.

Мы говорим о догадке потому, что формула, получаемая при помощи конечных разностей, может оказаться «ограниченно применимой» — порождать лишь часть членов бесконечной последовательности. Применимость формулы «конечно-разностного происхождения» ко всем без исключения членам числовой последовательности каждый раз необходимо доказывать особо. В случае круглого пирога такое доказательстве действительно существует. Его нетрудно найти, если воспользоваться методом математической индукции.

После этих замечаний, носящих сугубо предварительный характер, вы достаточно вооружены, чтобы смело вступить на неизведанную территорию и проложить по ней десятки увлекательных маршрутов в самых разных направлениях, многие из которых приводят к необычным числовым последовательностям, формулам и доказательствам методом математической индукции. Определить максимальное число частей, на которые можно разделить:

1) подковообразный пирог n прямыми;

2) головку сыра в форме шара или цилиндра n плоскими разрезами;

3) пирог n круговыми разрезами, проводимыми специальным ножом;

4) пирог, испеченный в форме кольца (с круглым отверстием посредине) n прямыми;

5) бублик (тор) n плоскими разрезами.

Во всех этих задачах предполагается, что разрезы проводятся одновременно. Как изменятся ответы, если будет разрешено проводить разрезы последовательно и после каждого разреза перекладывать образовавшиеся куски?