Мисс Евклид поставила на кафедру большой деревянный куб.
Мисс Евклид. Сегодня я проведу с вами контрольную. Я задам вам всего 3 вопроса об этом кубе. Мисс Евклид. Этот куб можно распилить на 64 единичных куба. Для этого требуется провести 9 разрезов. Мисс Евклид. Если бы перед каждым
разрезом части куба разрешалось бы перекладывать, то можно было бы
ограничиться 6 разрезами. Мой первый вопрос к вам: как доказать, что
число разрезов не может быть меньше 6? Пока класс трудился над ответом на первый
вопрос, мисс Евклид провела на двух гранях куба диагонали, проходящие
через общую вершину.
Мисс Евклид. Мой следующий вопрос: чему равен угол между этими двумя диагоналями? Прежде чем задать свой третий вопрос, мисс Евклид положила на верхнюю грань куба линейку.
Мисс Евклид. Как с помощью этой линейки проще всего измерять длину диагонали куба АВ?
На сколько вопросов мисс Евклид вы смогли бы ответить? Я смог ответить на 2 из 3 вопросов.
Каверзные задачи
Решение задачи 1. Докажем, что куб
4×4×4 невозможно разрезать на 64 кубика менее чем 6 плоскими разрезами
(при условии, что после каждого разреза части куба разрешается
перекладывать). Рассмотрим для этого любой из 8 внутренних кубиков. Ни
один из внутренних кубиков не имеет «готовых» граней, которые бы
совпадали с гранями большого куба. Следовательно, каждую из 6 граней
внутреннего куба необходимо выделить, для чего требуется провести 1
плоский разрез. Поскольку ни одна плоскость не может выделить более
одной грани куба, то число разрезов, которые необходимо провести, чтобы
высечь все 6 граней куба, должно быть не меньше 6.
Существует ли общий метод, позволяющий
распилить любой прямоугольный параллелепипед с целочисленными длинами
ребер на единичные кубы при минимальном числе разрезов (части
параллелепипеда разрешается переставлять)? Да, такой метод существует и
заключается в следующем. Рассмотрим 3 разных куба, длины ребер которых
равны длине, ширине и высоте параллелепипеда. Для каждого куба определим
минимальное число разрезов, которые необходимо провести, чтобы
разделить его на слои единичной толщины. Для этого проведем плоский
разрез перпендикулярно ребру куба через целую точку, расположенную как
можно ближе к середине ребра (если в длине ребра укладывается четное
число единиц, то распил делит ребро пополам; если же в длине ребра
укладывается нечетное число единиц, то распил проходит на расстоянии
половины единицы длины от середины ребра), переложим полученные части и
будем повторять всю процедуру до тех пор, пока весь куб не распадется на
слои единичной толщины. Сумма трех минимумов (по одному для каждого
ребра) даст нам ответ задачи.
Например, чтобы распилить на единичные
кубики прямоугольный параллелепипед 3×4×5, необходимо провести 7 плоских
разрезов: 2 для ребра 3, 2 для ребра 4 и 3 для ребра 5. Доказательство
этого алгоритма было впервые опубликовано в журнале Mathematics Magazine
в 1952 г.
Решение задачи 2. Задача решается
просто, если сообразить, что на еще одной грани куба можно провести
третью диагональ, соединяющую концы диагоналей, проведенных мисс Евклид
(рис. 16). Три диагонали образуют равносторонний
треугольник. Так как каждый из углов равностороннего треугольника равен
60°, то и угол между проведенными мисс Евклид диагоналями равен 60°.
Вторая задача мисс Евклид допускает изящное
обобщение. Предположим, что мисс Евклид провела на поверхности куба две
прямые, соединяющие середины A, B и C трех ребер (рис. 17). Чему равен угол ABC между этими прямыми? Решение задачи находим по аналогии с
предыдущим решением. Прежде всего соединим отрезками прямых середины
ребер на четырех остальных гранях так, чтобы все шесть отрезков
образовали замкнутую ломаную. Ясно, что все шесть отрезков имеют
одинаковую длину и углы между любыми двумя смежными отрезками также
одинаковы. Следовательно, если бы нам удалось доказать, что все шесть
вершин ломаной лежат в одной плоскости, то мы могли бы утверждать, что
наша шестизвенная замкнутая ломаная имеет форму правильного
шестиугольника. Доказать нужное нам утверждение нетрудно, но в его
справедливости вы можете убедиться экспериментально, распилив деревянный
куб на две половинки вдоль плоскости, проходящей через середины шести
ребер.
То, что поперечное сечение, делящее куб на
две половины, может иметь форму правильного шестиугольника, неожиданно и
в какой-то мере противоречит интуиции. Ну, а коль скоро мы знаем, что
две проведенные мисс Евклид линии являются двумя смежными сторонами
правильного шестиугольника, то найти угол между ними не составляет
никакого труда: он равен 120°.
Рис. 17 наводит на мысль о еще одной интересной задаче. Предположим, что муха хочет проползти по поверхности куба из точки A в точку C. Можно ли считать путь, образованный отрезками AB и BC, кратчайшим?
Эту задачу легко и просто решит тот, кто догадается, что кратчайший путь из точки A в точку B
на поверхности куба можно найти, если две смежные грани куба развернуть
так, чтобы их плоскости совпали: кратчайшим будет отрезок прямой,
соединяющий на развертке точки A и C. Развернуть две
смежные грани куба так, чтобы плоскости их совпали, можно двумя
способами, выбрав либо переднюю и верхнюю грань, либо переднюю и правую
грань, поэтому при решении задачи необходимо соблюдать осторожность. В
первом случае мы получаем путь длиной √2, во втором — путь длиной
√2,5.Следовательно, на рис. 17 изображен кратчайший путь на поверхности куба из A в C.
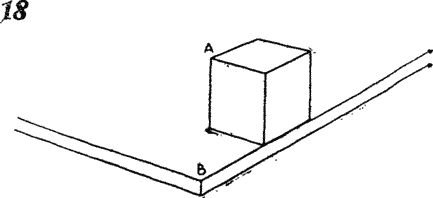
Решение задачи 3. Разумеется, длину
диагонали куба можно определить, измерив линейкой длину ребра и дважды
применив теорему Пифагора. Но диагональ куба можно измерить линейкой
гораздо более простым способом. Поставив куб на край стола, отмерим
отрезок, равный по длине ребру куба, и концы отрезка пометим, после чего
сдвинем куб на длину ребра вдоль края стола (рис. 18). Расстояние от A до B в точности равно диагонали куба, и его можно измерить линейкой.
Как вы стали бы измерять радиус большого
шара, если бы у вас под рукой была только линейка, длина которой
составляет ⅔ от диаметра шара? Один из простых способов состоит в том,
чтобы запачкать шар сажей или губной помадой и прижать его к стене так,
чтобы на стене в точке касания осталась отметка. Измерив линейкой
расстояние от пола до отметки, вы определите радиус шара. Можете ли вы
предложить аналогичные методы, позволяющие при помощи какого-нибудь
ухищрения измерить высоту конуса или пирамиды? Можете ли вы точно
измерить радиус цилиндрической трубы, если под рукой у вас имеется
только плотницкий угольник?
| 
