Знаменитый игрок Дэн, по прозвищу Ставлю Доллар, сидел в баре со своим другом Диком, по профессии пилотом. Дэн. Дик, ставлю доллар, что ты не
сможешь решить простой задачки. Самолет пролетает 100 км, держа курс на
юг, затем 100 км на восток и 100 км на север, после чего оказывается в
исходной точке. Откуда он вылетел? Дик. Принимаю пари, Дэн. Задачка твоя давно известна. Самолет вылетел с Северного полюса.
Дэн. Правильно. Держи доллар. Ставлю еще доллар, что ты ни за что не догадаешься, откуда еще мог вылететь самолет. Дик погрузился в размышления. Дик. Другой точки, кроме Северного
полюса, нет и быть не может, и я берусь доказать это. Предположим, что
самолет вылетает из точки, расположенной между Северным полюсом и
экватором. Дик. Ясно, что в этом случае
конечная точка маршрута не может совпадать с исходной. Если же самолет
вылетает из точки, расположенной на экваторе, то конечная точка маршрута
оказывается примерно в 100 км от исходной точки. Дик. Если же самолет вылетает из
точки, расположенной в южном полушарии, то конечная точка будет отстоять
от исходной более чем на 100 км. Дэн. Может, ты хочешь поспорить на 2 доллара, что самолет не мог вылететь ниоткуда, кроме Северного полюса?
Дик принял пари и проиграл. Почему? Предположим, что самолет стартовал из
точки, расположенной на параллели А, отстоящей на расстояние 116 км от
Южного полюса, и пролетел к югу 100 км. Пролетев 100 км на восток, он совершит
полный оборот вокруг Южного полюса. Пролетев затем 100 км на север, он
непременно вернется в исходную точку. Дик. Ты прав, вот твои 2 доллара.
Дэн. Ставлю еще доллар, что,
по-твоему, я не смогу указать других мест на земном шаре, вылетев откуда
и пролетев сначала 100 км на юг, затем 100 км на восток и 100 км на
север, самолет сможет вернуться в исходную точку. Под «другими местами» я
понимаю точки, не лежащие на параллели А и не совпадающие с Северным
полюсом. Дик. Тогда ставлю 50 долларов, что таких точек на земном шаре нет. Бедный Дик снова проиграл. Какую важную идею он упустил из виду?
Откуда вылетать?
Заключая второе пари, Дик упустил из виду
весьма важное обстоятельство: точка, откуда вылетает самолет, может быть
выбрана так близко от Южного полюса, что, пролетев 100 км на восток, он
опишет вокруг полюса не один оборот, как в предыдущем решении, а два
полных оборота. Так возникает новая параллель, все точки которой служат
решениями исходной задачи. Аналогичным образом самолет может вылететь из
любой точки еще меньшей окружности и, держа курс на восток, совершить
три, четыре и т. д. оборота вокруг полюса. При любом целом
положительном n можно указать соответствующую параллель, вылетев из любой точки которой и держа курс на восток, самолет совершит n
оборотов вокруг полюса. Следовательно, точки, из которых может вылететь
самолет, заполняют бесконечно много параллелей, стягивающихся к полюсу,
А вот еще одна навигационная задача,
связанная с замечательной кривой на сфере — локсодромой, или линией
постоянного курса. Самолет вылетает из точки, расположенной на экваторе,
и берет курс на северо-восток. Где закончится его полет, если запасы
горючего можно считать неограниченными? Какова длина маршрута и как он
выглядит?
Возможно, вы удивитесь, когда узнаете, что
маршрут полета имеет вид спирали, пересекающей все меридианы под одним и
тем же углом и заканчивающейся на Северном полюсе. Такую кривую
правильнее было бы рассматривать как винтовую линию, навитую на сферу,
стягивающуюся к Северному полюсу и успевающую описать вокруг полюса
бесконечно много витков. Если самолет условно принять за точку, то
маршрут, хотя и успевает совершить бесконечно много оборотов вокруг
полюса, имеет конечную длину, которая поддается вычислению.
Следовательно, поддерживая в полете постоянную скорость, самолет
достигнет Северный полюс за конечное время.
При нанесении на плоскую карту форма
локсодромы искажается в зависимости от выбора картографической проекции.
На меркаторской проекции, известной по карте мира, локсодрома переходит
в прямую. Именно поэтому меркаторская проекция находит столь широкое
применение в решении навигационных задач. Если судно или самолет следуют
постоянным курсом, то, чтобы проложить его на карте, достаточно
провести прямую.
А что произойдет, если самолет, взлетев с
Северного полюса, возьмет курс на юго-запад? Эта задача обратна
предыдущей. Полет, как и прежде, будет происходить по локсодроме, но
сказать, где приземлится самолет в конце пути, мы не можем. В этом можно
легко убедиться, обратив время: из какой бы точки, расположенной на
экваторе, ни вылетел самолет, он, двигаясь вспять, неизменно окажется на
Северном полюсе. Если же самолет, достигнув экватора, пересечет его и
будет лететь тем же курсом, то локсодрома стянется к Южному полюсу.
При проецировании на плоскость, касательную
к полюсу (и параллельную плоскости экватора), локсодрома переходит в
равноугольную, или логарифмическую, спираль. Эта спираль пересекает
радиус-вектор под постоянным углом.
Задача о четырех жуках, входит в
сокровищницу занимательной математики. Она также связана с построением
маршрутов и логарифмической спиралью, но допускает неожиданно простое
решение, избавляющее от необходимости производить утомительные выкладки.
Вы познакомитесь с ней, прочитав небольшой рассказ о семействе Пицца и
их любимцах — четырех черепашках.
Том Пицца, тренер и художественный руководитель черепашек, выдрессировал своих питомцев так, что Абнер (A) всегда полз к Берте, Берта (B) — к Чарлзу, Чарлз (C) — к Далиле (D) и Далила — к Абнеру. Однажды он расставил черепашек по углам квадратной комнаты так, что они образовали вершины квадрата ABCD, включил секундомер и принялся наблюдать за тем, что произойдет.
— Интересно получается, сынок, — сказал
мистер Пицца. — Каждая черепашка ползет прямиком к своему соседу справа.
Все черепашки движутся с одинаковой скоростью и поэтому в любой момент
времени находятся в вершинах некоторого квадрата (рис. 9). — И квадрат этот все время поворачивается и уменьшается, — добавил Том. — Смотри! Видишь? Черепашки сошлись в центре!
Предположим, что каждая черепашка ползет с
постоянной скоростью 1 см/с и что комната, где они находятся, имеет
форму квадрата со стороной 3 м. Через сколько времени черепашки
встретятся в центре комнаты? (Каждую черепашку мы условно принимаем за
точку.)
Мистер Пицца попытался было решить задачу,
интегрируя по траектории черепашки, и уже достал из кармана
программируемый микрокалькулятор последней модели, как вдруг миссис
Пицца воскликнула:
— Не нужно никакой высшей математики,
Пеппероне! Задача решается очень просто! Черепашки встречаются в центре
комнаты через 5 мин.
Какая идея пришла в голову миссис Пицца?
Рассмотрим каких-нибудь двух черепашек,
расположенных в двух соседних вершинах квадрата, например Абнера и
Берту. В каждый момент Берта движется под прямым углом к Абнеру,
ползущему к ней, так как Абнер всегда ползет к Берте, а Берта всегда
ползет к Чарлзу. Именно поэтому черепашки все время находятся в вершинах
квадрата. Поскольку Берта никогда не ползет к Абнеру и не уползает от
него, то ее движение не увеличивает и не уменьшает разделяющее их
расстояние и при подсчете времени движением можно пренебречь. Дело
обстоит так, как если бы Берта оставалась в своем углу комнаты, а Абнер
полз к ней вдоль стенки.
В этом и состоит ключ к решению задачи.
Криволинейный путь Абнера должен совпадать по длине со стороной
начального квадрата, а так как эта сторона равна 300 см и Абнер ползет
со скоростью 1 см/с, то он доползет до Берты за 300 с, или 5 мин. То же
можно сказать и о всех остальных черепашках. Следовательно, все
черепашки встречаются в центре комнаты по истечении 5 мин.
При помощи микрокалькулятора можно
построить траектории черепашек — кривые, описываемое вершинами
вращающегося и одновременно сжимающегося квадрата, если нанести на
диаграмму последовательные положения вершин через определенные
промежутки времени. Результат такого рода выкладок представлен на рис. 10.
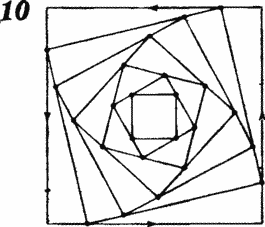
Можете ли вы обобщить задачу на случай,
когда в исходной позиции точки расположены в вершинах любого правильного
многоугольника? Начните с равностороннего треугольника, затем перейдите
к правильному пятиугольнику и т. д. Можете ли вы указать общую формулу,
позволяющую по известной длине стороны исходного многоугольника
вычислять длину пути? Что произойдет в предельном случае, когда
бесконечно много точек (черепашек) начинают двигаться по направлению к
своим соседям справа (или слева) и вершин многоугольника с бесконечным
числом сторон? Встретятся ли они когда-нибудь? Предположим теперь, что
исходные многоугольники неправильные. Что произойдет, например, если
четыре черепашки займут исходные позиции в вершинах прямоугольной, а не
квадратной комнаты?
Предположим, что черепашки Тома Пиццы после
встречи в центре комнаты расползаются, причем каждая из них движется по
прямой от своего соседа слева? Можно ли утверждать, что черепашки
непременно расползутся по углам комнаты?
| 
