На заседании шахматного клуба мистер Бишоп предложил следующую задачу.

Мистер Бишоп. Как поменять позиции черных и белых коней за наименьшее число ходов?

Один из членов клуба сделал 2 первых хода так, как показано на диаграмме. Переставить белых коней в верхние углы доски, а черных — в нижние он сумел за 24 хода.

Другому члену клуба удалось решить задачу мистера Бишопа за 20 ходов.

Но никому не удавалось решить задачу менее чем за 18 ходов, пока не появилась Фанни Фиш.

Мисс Фиш. Есть идея! Я знаю, как решить задачу за 16 ходов, и могу доказать, что ее нельзя решить за меньшее число ходов.

Прежде чем приступить к объяснению, Фанни начертила диаграмму, на которой отрезками прямых изображены возможные ходы каждого коня.

Мисс Фиш. Представьте себе, что отрезки прямых — это нити, а восемь клеток нанизаны на них, как бусины, и их можно расположить по окружности.

Мисс Фиш. Каждый ход на доске соответствует вполне определенному ходу на окружности. Чтобы поменять позиции коней, их необходимо переместить по окружности, двигая в одном направлении.

Мистер Бишоп. Вы совершенно правы, Фанни. Чтобы перейти на новую позицию, каждый из 4 коней должен совершить по 4 хода. Таким образом, задачу можно решить за 16 ходов, а более экономного решения не существует.

Фанни заменила одного из белых коней красным и задала членам шахматного клуба новую задачку: как поменять местами белого и красного коня за наименьшее число ходов?

Как, по-вашему, почему Фанни улыбалась, предлагая эту задачку?

Шахматные кони и звездчатые фигуры

Фанни решила шахматную задачу, сведя ее к изоморфной задаче, допускавшей простое (хотя и далеко не тривиальное!) решение. Поставленную Фанни задачу можно решить тем же методом. Соединив нитями клетки, занятые конями, и развернув получившееся «ожерелье» в окружность, мы увидим, что кони нанизаны на нити в следующем порядке: черный, черный, красный, белый. Фанни улыбалась, так как понимала, что переставить красного и белого коней невозможно: они следуют друг за другом в неизменном порядке, потому что ни один конь не может перепрыгнуть через другого коня, если они оба движутся по кругу (в любом направлении) и обгон запрещен. Понятно ли вам почему?

При движении по окружности по часовой стрелке белый конь всегда следует непосредственно за красным. Если бы белый и красный кони могли поменяться полями, которые они занимали на доске с самого начала, то порядок следования был бы изменен на обратный и красный конь двигался бы по кругу непосредственно за белым. Ясно, что такое перестроение невозможно. Действительно, оно означало бы, что один из коней (либо белый, либо красный) перепрыгнул через двух черных коней. Сведя мини-шахматную задачу к топологической задаче о расположении четырех точек на простой замкнутой кривой, мы получили возможность весьма просто доказать, что решения исходной задачи не существует. Получить доказательство «несуществования» другим способом было бы чрезвычайно трудно. Попробуйте, и вы убедитесь в этом сами.

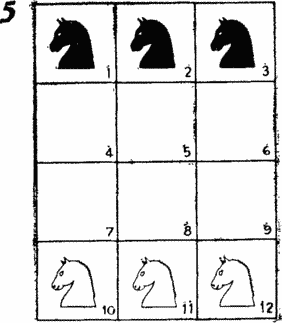
Вам понравилась задача о перестановке шахматных коней? Вот еще одна такая задача, по трудности даже превосходящая обе предыдущие. Рассмотрим позицию на шахматной доске 3×4, изображенную на рис. 5. Как и прежде, трех черных и трех белых коней требуется поменять местами так, чтобы белые кони оказались на верхней горизонтали, а черные заняли нижнюю горизонталь, причем выполнить перестановку за наименьшее число ходов.

В этом случае, как видно на рис. 6, изоморфный граф более сложен. Этот граф представляет собой диаграмму, на которой показаны все возможные ходы коней, Предположив, что вершины нашего графа — пуговицы или бусины, а ребра — нити, мы обнаружим, что развернуть его в окружность, как в предыдущей задаче, невозможно, но наш граф из нитей и пуговиц нам удастся уложить так, как показано на рис. 7. Числа на этом рисунке соответствуют номерам клеток на рис. 4 и 5.

Ясно, что задача о перестановке шахматных коней на этом графе изоморфна исходной задаче, но решается несравненно легче. Удастся ли вам найти минимальное решение в 18 ходов?

Метод нитей и пуговиц позволяет проанализировать одну старинную игру. Для нее нам понадобится особая «доска» — звездчатый граф, изображенный на рис. 8, и семь монет или небольших фишек.

Игра состоит в следующем. Положив монету на любую вершину графа, вы можете сдвинуть ее вдоль черной ломаной линии (ребер графа) в любую другую вершину. После того как ход закончен, прикасаться к монете и перемещать ее в другую вершину запрещается.

Затем вы кладете вторую монету на любую незанятую вершину графа и передвигаете ее вдоль ребер в любую другую незанятую вершину. Так вы продолжаете действовать до тех пор, пока все семь монет не займут свое место на вершинах графа.

Очень скоро вы обнаружите, что расставить все семь монет удается, если действовать по тщательно продуманному плану: малейшая небрежность приводит к позиции, не позволяющей достичь в игре успеха. Не могли бы вы указать, каких правил следует придерживаться при расстановке и перемещении монет, чтобы вам неизменно сопутствовал успех?

Звездчатый граф можно полностью «раскрыть» подобно графам в двух первых задачах о перестановке шахматных коней, его удается развернуть в окружность. После того как это сделано, семь монет нетрудно расположить на окружности и проанализировать, как они могут двигаться. Справиться с этой задачей можно многими способами. Одна из наиболее простых выигрышных стратегий состоит в том, чтобы делать любой ход первой монетой, а все следующие монеты ставить и передвигать всегда так, чтобы по окончании хода они заняли вершину, которую занимала в исходном положении предыдущая монета.

Предложите сыграть в эту игру своим друзьям. Лишь очень немногие из них смогут расставить все семь монет, даже если вы один раз быстро продемонстрируете им, как следует играть.

Невиданный меч

Присмотритесь повнимательнее к этой картинке. Что художник нарисовал неправильно?

Взгляните на меч в руке рыцаря: его невозможно вложить в ножны.

Эти два меча (если только они не имеют утолщений) можно вложить в ножны соответствующей формы. Можете ли вы придумать еще какую-нибудь форму для меча и парных ему ножен?

Вам пришла в голову мысль перейти от плоских кривых к пространственным? Оказывается, помимо двух традиционных форм мечей, вкладывающихся в ножны, тем же свойством обладают только мечи, выкованные в форме винтовой линии.

Незаменимая кривая

Винтовая линия играет важную роль в современной науке, — особенно в биологии и физике элементарных частиц. Молекулы ДНК имеют форму винтовой линии. В отличие от своих одно- и двумерных двоюродных сестер — прямых и окружностей — винтовая линия обладает «закрученностью», то есть может быть правой и левой. Прямая и окружность неотличимы от своих зеркальных отражений, но отличить винтовую линию от ее зеркального отражения не составляет ни малейшего труда. В зеркале винтовая линия, по выражению Алисы из Зазеркалья (Льюис Кэрролл), «идет наоборот».

Существует множество примеров винтовых линий в природе и в повседневной жизни. Винтовая линия по традиции считается правой, если она закручивается по часовой стрелке по мере удаления от вас. Винты, болты и гайки, как правило, имеют правую нарезку. Винтовые лестницы, стебли сахарного тростника, пружины, волокна в канатах и кабелях и стружки могут закручиваться как вправо, так и влево.

К числу примеров встречающихся в природе винтовых линий относятся рога многих животных, раковины морских моллюсков, гигантский зуб нарвала, ушная раковина человека, пуповина. В мире растений винтовая линия встречается в строении стеблей, побегов, усиков, семян, цветов, шишек, листьев и т. д. Взбираясь на вершину дерева или спускаясь с нее, белка описывает винтовую линию. Вылетая из пещеры, летучие мыши также движутся по винтовым линиям. Винтовые линии, навитые на конус, можно без труда обнаружить в таких атмосферных явлениях, как вихри или смерчи. Вода, стекая в раковине, также закручивается в воронку, сотканную из винтовых линий. Много других примеров винтовых линий вы найдете в книге М. Гарднера «Этот правый, левый мир».

Правильная винтовая линия — это кривая, навитая на круговой цилиндр под постоянным углом к образующим (напомним, что образующими называются прямые на поверхности цилиндра, параллельные его оси). Пусть ϑ — угол, под которым винтовая линия пересекает образующие цилиндра. При ϑ = 0° винтовая линия, как нетрудно видеть, вырождается в прямую, а при ϑ = 90° — в окружность.

Аналитически в этом можно удостовериться, если записать параметрические уравнения винтовой линии и проварьировать входящий в них угол ϑ от 0° до 90°. И прямая, и окружность — предельные формы более общей пространственной кривой, получившей название винтовой линии. Правильная винтовая линия — единственная пространственная кривая постоянной кривизны. Этим и объясняется, почему мечи, вкладывающиеся в ножны, можно изготовить только в форме правильной винтовой линии (что выглядело бы несколько необычно) и двух ее предельных случаев — прямой и окружности.

Проекция винтовой линии на плоскость, перпендикулярную ее оси, имеет форму окружности. Спроецировав винтовую линию на плоскость, параллельную оси, мы получим синусоиду. В этом нетрудно убедиться, если снова воспользоваться параметрическими уравнениями кривой. Многие свойства синусоиды можно изучать по ее близкой родственнице — винтовой линии.

В этой связи мы хотим рассказать одну забавную историю-задачу, допускающую (при надлежащем подходе) очень простое решение. Внутри цилиндрической башни высотой 100 м ходит лифт. Снаружи башни имеется винтовая лестница, образующая с вертикалью постоянный угол ϑ = 60°. Диаметр башни 13 м.

Однажды мистер и миссис Пицца поднялись на лифте на смотровую площадку, расположенную на вершине башни. Их сын Томато Пицца предпочел идти наверх пешком. Когда он добрался до смотровой площадки, вид у него был не блестящий.

— Не мудрено, что ты устал, сынок, — заметил мистер Пицца. — Ведь тебе пришлось проделать вчетверо больший путь, чем нам, и все пешком.

— Ты ошибаешься, папа, — ответил Том. — Я прошел лишь вдвое больший путь, чем вы проехали.

Кто прав: Том или его отец?

Кое-кто склонен думать, будто для того, чтобы вычислить длину винтовой лестницы, необходимо знать диаметр башни. В действительности информация о диаметре башни совершенно лишняя!

Дело в том, что винтовую лестницу можно развернуть в гипотенузу прямоугольного треугольника с острым углом 30° и высотой 100 м, а гипотенуза такого треугольника вдвое больше высоты (катета, лежащего против угла 30°), Следовательно, прав был Том.

Убедиться в этом вы можете, развернув какую-нибудь картонную трубку. Возможно, исход эксперимента несколько удивит вас: вы увидите, что длина шва (винтовой линии, как бы навитой на трубку) не зависит от диаметра цилиндра, в который скручен прямоугольный треугольник.