Проф. Слог. Ваше первое задание, мистер Рите, связано с этой таблицей, на которой выписаны четыре имени. Приз за успешное выполнение задания — 6 коробок превосходных кубинских сигар.

Проф. Слог. Проведя 3 линии, мы легко можем разделить таблицу на 4 графы так, чтобы в каждой из них было вписано только 1 имя. Нельзя ли добиться того же с помощью 2, а не 3 линий?

Мистер Рите молча попыхивал сигарой, пока его время не истекло.

Мистер Рите. Этого сделать нельзя!

Проф. Слог. Вы заблуждаетесь, мистер Рите. Задача решается очень просто. Должно быть, сигарный дым затуманил ясность вашего мышления.

Честно и прямо

Задача проф. Слога решается сразу, стоит лишь догадаться, что каждое имя можно разбить на две части, а из «осколков», комбинируя их в других сочетаниях, составить те же четыре имя.

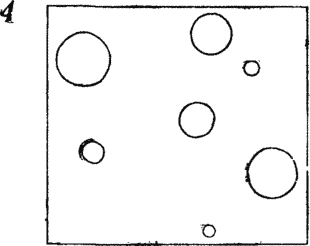
Идея разбиения на части прямыми встречается и во многих других головоломках. Обычно речь идет о том, чтобы несколькими прямыми разделить ту или иную картинку на части, каждая из которых содержала бы лишь одну деталь. Типичная головоломка такого рода изображена на рис. 4. Можете ли вы провести 3 прямые так, чтобы каждый кружок оказался отрезанным от всех остальных? Решение оказывается неожиданно простым, если догадаться, что части, на которые рассекают квадрат 3 прямые, не обязательно должны быть прямоугольниками и что 3 прямыми квадрат можно разделить на 7 частей.

Интересные варианты той же идеи возникают, если вместо кружков взять числа. Требуется разделить квадрат прямыми на части так, чтобы в каждой части числа обладали каким-нибудь общим отличительным свойством. Свое искусство в решении задач этого типа вы можете испытать на следующей головоломке (рис. 5). Требуется провести 4 прямые так, чтобы они разделили квадрат на 11 частей и сумма чисел в каждой части была равна 10. Решение этой задачи приведено в конце книги.