Больше всего на свете Боб и Элен любили всякого рода головоломки. Особенно им нравилось ставить в тупик друг друга и своих друзей каверзными вопросами.

Однажды, когда Боб и Элен проезжали мимо магазина грампластинок, Боб задал Элен вопрос.

Боб. Ты все еще собираешь пластинки с джазовой музыкой?

Элен. Нет, половину всех пластинок и еще полпластинки я подарила Сьюзен.

Элен. Половину оставшихся пластинок и еще полпластинки я подарила Джо.

Элен. После этого у меня осталась одна пластинка. Я подарю ее тебе, если ты скажешь, сколько пластинок было у меня в коллекции до того, как я начала ее раздавать.

Боб не сразу смог решить задачу, так как не мог понять, зачем Элен понадобилось дарить друзьям половинки пластинок.

Внезапно его осенила блестящая мысль, и он понял, что ни одна пластинка не была разбита на половники. Боб ответил на вопрос Элен, и та подарила ему последнюю пластинку из своей коллекция.

Какая мысль пришла Бобу в голову?

Половинки целого

Неужели вы попались в ловушку и не подумали, что половина чего-то и ½ могут оказаться целым числом? Если да, то, должно быть, попытались решить задачу, ведя счет на половинки грампластинок, и, запутавшись вскоре в вычислениях, оставили затею как безнадежную. Неожиданно простым решение получается, если догадаться, что половина от нечетного числа и еще половина равны целому числу.

По словам Элен, у нее после того, как она преподнесла свой второй подарок, осталась 1 пластинка. Значит, до того, как она подарила часть своих пластинок Джо, у нее должны были остаться 3 пластинки. Половина от 3 составляет 3/2, а 3/2 + 1/2 = 2, поэтому Элен подарила Джо 2 пластинки, после чего у нее осталась 1 пластинка. Продолжая решать задачи «задним ходом», нетрудно установить, что сначала у Элен было 7 пластинок и что 4 пластинки она подарила Сьюзи.

Разумеется, задачу можно было бы решать и алгебраически. Составление и решение соответствующего уравнения — превосходное упражнение по элементарной алгебре. Удивительно, что такая простая задача приводит к такому сложному уравнению:

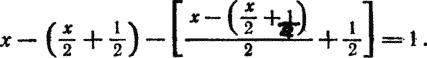
Новые головоломки того же типа мы получим, варьируя параметры задачи. Предположим, например, что Элен каждый раз дарит кому-нибудь половину своих пластинок и еще полпластинки, проделывает это не дважды, а трижды и остается не с одной пластинкой, а без единой пластинки. Сколько пластинок было у нее сначала? Возможно, вам покажется странным, что ответ остается прежним — 7 пластинок, но удивительного здесь ничего нет: в третий раз Элен дарит последнюю оставшуюся у нее пластинку. А сколько пластинок было у нее сначала, если она дарит каждый раз половину своих пластинок и еще полпластинки и проделывает эту процедуру 4 раза, после чего у нее остается 1 пластинка? А если Элен дарит пластинки 5 раз? Какого рода последовательность порождают возникающие в этой серии задач числа?

Долю, которую составляют отобранные для очередного подарка пластинки, также можно изменять. Предположим, что Элен отдает каждый раз треть своих пластинок и еще треть пластинки и после того, как она преподносит 2 подарка, у нее остается 3 пластинки. Сколько пластинок было у Элен сначала? Существует ли решение задали в том случае, если процедуру усечения коллекции на одну треть и еще треть пластинки Элен повторяет трижды, после чего у нее остаются 3 пластинки? Варьируя параметры задачи (число подарков, долю, которую составляют отобранные для очередного подарка пластинки, и число оставшихся у Элен пластинок), вы обнаружите, что решение существует не всегда, то есть не всегда возникает необходимость дарить часть пластинки. При каких ограничениях в задачах этого типа необходимость дарить пластинки «частями» вообще отпадает?

Доля, которую осколки «разбитой» пластинки составляют от целого, может варьироваться от подарка к подарку. Вот, например, задача, в которой эта доля не остается постоянной.

Один мальчик с увлечением занимался разведением золотых рыбок, потом это занятие ему надоело и он решил продать всех своих рыбок. Свое решение он осуществил в 5 этапов:

1. Продал половину всех своих рыбок и еще полрыбки.

2. Продал треть оставшихся рыбок и еще треть рыбки.

3. Продал четверть оставшихся рыбок и еще четверть рыбки.

4. Продал пятую часть оставшихся рыбок и еще одну пятую рыбки.

После этого у него осталось 19 рыбок. Разумеется, с золотыми рыбками он обращался бережно и ему и в голову не приходило делить рыбку на части. Сколько рыбок было у мальчика сначала? Ответ: 101 рыбка, но решить эту задачу не так просто, как предыдущие. Попробуйте и вы убедитесь в этом сами.

А вот еще одна разновидность задач того же типа.

У одной дамы было в сумочке несколько купюр достоинством в 1 доллар каждая. Других денег у нее с собой не было.

1. Половину денег дама израсходовала на покупку новой шляпки, а 1 доллар заплатила за освежающий напиток.

2. Зайдя в кафе позавтракать, дама израсходовала половину оставшихся у нее денег и еще 2 доллара заплатила за сигареты.

3. На половину оставшихся у нее денег она купила книгу и по дороге домой зашла в бар и заказала коктейль за 3 доллара, после чего у нее остался 1 доллар. Сколько долларов было у нее первоначально, если предположить, что ей ни разу не пришлось разменивать долларовые купюры?

Ответ приведен в конце книги.

Заметим, что во всех вариантах в условиях задачи непременно говорится, сколько грампластинок, золотых рыбок или купюр остается у действующего лица по окончании всех перипетий. Во многих случаях ответ задачи можно получить и без такой информации, но для этого пришлось бы решать в целых числах некоторые неопределенные уравнения. Наиболее известная задача такого рода легла в основу рассказа американского писателя Бена Эймса Уильямса «Кокосовые орехи».

Действие рассказа происходит на острове, на который после кораблекрушения попадают 5 человек и 1 обезьяна. Первый день они собирают кокосовые орехи. Ночью один из людей просыпается и решает забрать причитающуюся ему долю орехов. Он раскладывает орехи на 5 одинаковых кучек, отдает лишний орех обезьяне и, спрятав свою долю, укладывается снова спать.

Вскоре просыпается другой товарищ по несчастью и проделывает то же самое: раскладывает орехи на 5 одинаковых кучек, отдает оставшийся орех обезьяне и, спрятав свою долю, укладывается снова спать. Затем по очереди просыпается третий, четвертый и пятый невольный обитатель острова, и каждый делает то же, что и первые два. Утром вся пятерка делит оставшиеся орехи на 5 равных частей. На этот раз ни одного лишнего ореха не остается.

Сколько кокосовых орехов было собрано первоначально?

Задача допускает бесконечно много решений. Наименьшее из них — 3121 орех. Решить задачу не очень просто.

Коль скоро мы заговорили о кокосовых орехах, я хочу предложить вам одну задачу, которую можно решить сразу. При расчистке джунглей было собрано 25 кокосовых орехов, обезьяна стащила все орехи, кроме 7, Сколько орехов осталось? Ответ: не 18.