В звоннице средневековой церкви сохранились две бесценные веревки, за которые звонари раскачивали колокола. Обе веревки проходят через небольшие отверстия в потолке комнаты звонарей. Потолок очень высокий. Расстояние между отверстиями 25 см, а диаметр каждого из них таков, что веревки свободно проходят сквозь них.

Тони, бывший акробат, вознамерился похитить веревки — отрезать от каждой из них кусок побольше.

Тони. Как назло, колокола на самом верху звонницы заперты на семь запоров. Проникнуть можно только в комнату звонарей.

Тони. Придется залезть по веревкам и отрезать от каждой из них кусок побольше. Жаль, до потолка здесь так высоко, что если я отрежу больше трети видимой части веревки, то упаду и сломаю себе шею.

Тони размышлял довольно долго, пока, наконец, не придумал, как похитить обе веревки почти целиком.

Что бы вы сделали на его месте?

Решение Тони было весьма остроумным. Прежде всего он связал свободные концы веревок. Затем залез по одной из них (обозначим ее A) под самый потолок.

Повиснув под потолком на веревке A, Тони перерезал веревку B примерно на полметра ниже потолка и свисающий из отверстия остаток связал в петлю.

Продев в петлю руку, Тони повис на веревке B и перерезал веревку A под самым потолком, приняв все меры предосторожности, чтобы отрезанный кусок веревки A не упал на пол. Затем он продел веревку A сквозь петлю и принялся протягивать ее, пока наверху не оказались связанные концы веревок A и B.

После этого Тони слез по сложенной вдвое веревке, выдернул ее из петли и ушел, унося с собой всю веревку A и почти всю веревку B.

А как бы вы это сделали?

Манипуляции с веревкой

Задачу, о которой вы узнали, прочитав рассказ о дерзком похитителе веревок, нельзя считать строго определенной, поэтому и решений у нее может быть несколько. Возможно, что приведенное нами решение наиболее «практично», но вы заведомо сумеете предложить еще несколько других вариантов, которыми мог бы воспользоваться вор. Не исключено, что ваше решение окажется лучше.

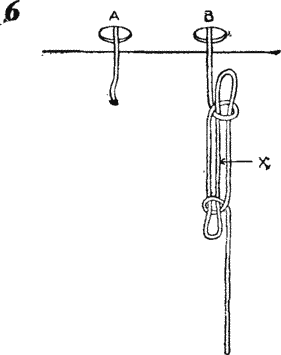
Например, похититель мог бы завязать на веревке В так называемую колышку — специальный узел, используемый моряками и альпинистами для временного укорочения снасти (рис. 6). Повиснув на веревке B, он мог бы обрезать веревку A под потолком (и дать ей упасть на пол), после чего перерезать веревку B в точке X. Всем альпинистам хорошо известно, что узел будет держать, пока вор не соскользнет по веревке B вниз. Дернув за веревку B, он распустит колышку и получит почти всю веревку B, за исключением небольшого ее куска под самым потолком.

Другое возможное решение. Похититель взбирается наверх по веревке A. Ухватившись одной рукой за веревку B и вися на веревке A, он начинает перерезать волокно за волокном веревку A, пока не почувствует, что та вот-вот оборвется. Затем он стягивает обе веревки вместе и вися на двух веревках одновременно, начинает перерезать веревку B под самым потолком так же, как он перерезал веревку A, и спускается по двум веревкам вниз. Каждая из веревок в отдельности не выдержала бы его веса, но с половинной нагрузкой веревки справляются благополучно. Очутившись на полу, вор сильным рывком обрывает веревки по месту надреза.

Третий способ предполагает, что отверстия в потолке достаточно велики. Сначала похититель связывает свободные концы веревок A и B у пола. Затем взбирается по веревке A, перерезает веревку B под потолком и проталкивает ее длинный конец в отверстие для веревки B, пока тот не покажется из отверстия для веревки A, после чего начинает протягивать веревку B до тех пор, пока ее конец не окажется у пола, а узел — под потолком у отверстия для веревки B. Ухватившись у самого потолка за веревку B, продернутую сквозь отверстие для веревки A, и нижнюю часть веревки A, подтянутую теперь к потолку, похититель перерезает верхнюю часть веревки A (торчащую из отверстия для веревки A) как можно выше и, спустившись по двойной веревке, сдергивает ее на пол.

А вот более хитроумный вариант предыдущего решения. Свободные концы веревок остаются не связанными. Похититель взбирается по веревке A, перерезает веревку B, проталкивает ее длинный конец сквозь отверстие для веревки B и вытягивает его из отверстия для веревки A, после чего захлестывает его вокруг веревки B и завязывают узлом (рис. 7). Повиснув на веревке B, похититель перерезает веревку A и привязывает конец ее к узлу. Спустившись по веревке B, он тянет за веревку A, веревка В проскальзывает сквозь петлю и падает вниз.

Еще один вариант. Похититель взбирается по веревке A и завязывает петлю на верхней части веревки B. Повиснув на этой петле, он перерезает веревку A, проталкивает ее конец сквозь отверстие для веревки A и вытягивает его из отверстия для веревки B, после чего привязывает к петле. Повиснув на двух веревках, он перерезает веревку B под потолком над петлей, спускается по двум веревкам вниз и, потянув за веревку B, сдергивает их вниз.

Некоторые из приведенных выше решений практически не осуществимы: если бы похититель вздумал воспользоваться любым из них, то колокола зазвонили бы и он был бы пойман с поличным. Одно из достоинств самого первого решения состоит в том, что похититель осторожно натягивая веревку B, прежде чем повиснуть на ней, мог бы избежать лишнего шума (колокол B при соблюдении всех мер предосторожности не зазвонил бы). Прежде чем влезть по веревке A, похитителю также следовало бы осторожно натянуть ее.

Во многих классических процедурных задачах, аналогичных задачам о переправах, фигурирует переброшенная через блок длинная веревка, к каждому концу которой прикреплено по корзине. Льюис Кэрролл очень любил следующий вариант такой задачи.

Пленная королева вместе со своим сыном и дочерью заточены в каморке на самом верху высокой башни. Снаружи у их окна прикреплен блок, через который перекинута веревка. На каждом конце веревки висит по корзине. Вес обеих корзин совершенно одинаков. Верхняя корзина, находящаяся как раз против окна темницы, пустая, в нижней корзине, достающей до земли, лежит камень массой 30 кг, служащий противовесом.

Блок сильно заржавел и вращается со скрипом достаточно медленно для того, чтобы спуск в корзине был безопасен для каждого, чья масса превышает массу противовеса не более чем на б кг. При большей разности масс удар о землю может причинить тяжкие увечья. Разумеется, если одна корзина поднимается, то другая опускается.

Масса королевы 78 кг, масса ее дочери 66 кг и масса сына 36 кг. Укажите простейший, то есть состоящий из наименьшего числа шагов, алгоритм побега. Корзины достаточно велики, чтобы вместить либо 2 людей, либо одного человека и камень. При побеге августейшим пленникам никто не помогает, и они не могут помочь себе, потянув за веревку. Иначе говоря, блок действует только в том случае, если масса в одной корзине превосходит массу в другой корзине.

Простейшее решение легко найти, если воспользоваться «аналоговым устройством»: написать массы на отдельных карточках и подвигать их вверх и вниз. Вам не удастся организовать побег всех трех узников менее чем за 9 шагов. Вот как выглядит наиболее экономичный алгоритм побега:

1. Сын вниз, камень вверх,

2. Дочь вниз, сын вверх.

3. Камень вниз.

4. Королева вниз, камень и дочь вверх.

5. Камень вниз.

6. Сын вниз, камень вверх,

7. Камень вниз.

8. Дочь вниз, сын вверх.

9. Сын вниз, камень вверх,

Задачи этого типа иногда усложняются введением животных, которые не могут самостоятельно влезать в корзины и вылезать из корзин. Льюис Кэрролл предлагает следующий вариант предыдущей задачи. На вершине башни вместе с королевой находились не только ее сын, дочь и груз, но и свинья массой 24 кг, собака массой 18 кг и кошка массой 12 кг. Спускать четвероногих нужно с теми же предосторожностями, что и людей, но теперь кто-нибудь непременно должен быть и наверху и внизу, чтобы класть животных в корзины и доставать их оттуда.

Удастся ли вам построить алгоритм побега короче 13 шагов? В обеих задачах тому, кто последним выйдет из корзины, следует поторапливаться, иначе он рискует получить по голове падающим противовесом!