1. Как разрезать тупоугольный треугольник на остроугольные? Пусть дан тупоугольный треугольник. Можно ли разрезать его на меньшие треугольники так, чтобы все они были остроугольными? (Остроугольным мы называем треугольник, у которого все три угла острые. Прямой угол, разумеется, не является ни тупым, ни острым.) Если этого сделать нельзя, докажите почему. Если можно, то возникает новый вопрос: каково наименьшее число остроугольных треугольников, на которые его можно разрезать?

На рис. 186 показана типичная безуспешная попытка решить задачу. Треугольник разбит на три остроугольных треугольника, но четвертый треугольник оказывается тупоугольным, поэтому три предыдущих разрезания ничего не дают.

 

Рис. 186 Можно ли разрезать этот треугольник на остроугольные треугольники меньших размеров?

Эта задача представляет большой интерес, потому что вводит в заблуждение и заставляет делать неверные заключения даже очень сильных математиков. Удовольствие, которое я получил, размышляя над ней, побудило меня поставить другой вопрос. Чему равно наименьшее число остроугольных треугольников, на которые можно разрезать квадрат? В течение нескольких дней я был убежден, что минимальное число равно девяти, но потом вдруг увидел, что его можно понизить до восьми. Интересно, сумеете ли вы найти решение с восемью треугольниками. Может быть, вам даже удастся улучшить мой результат и разрезать квадрат на еще меньшее число остроугольных треугольников. Я не смог доказать, что восемь — это минимум, хотя сильно подозреваю, что это так.

2. Чему равен один «лунар»? Герои романа Герберта Уэллса «Первые люди на Луне» обнаружили, что наш естественный спутник населен разумными насекомообразными существами, обитающими в пещерах под лунной поверхностью. Предположим, что эти существа пользуются единицей длины, которую мы назовем «лунаром». Она выбрана так, что площадь лунной поверхности, лунарах, в частности, совпадает с объемом Луны в кубических лунарах. Диаметр Луны составляет 3476 км.

Скольким километрам равен один лунар?

3. Игра в гугол. В 1958 году Джон Г. Фокс-младший и Л. Джеральд Марни изобрели необычную игру, которую они назвали «гугол». Играют в нее так. Попросите кого-нибудь взять сколько угодно небольших листочков бумаги и написать на них различные положительные числа (по одному числу на каждом листке). Числа могут быть любыми: от самых маленьких дробей до «гугола» — числа, состоящего из 1 и ста нулей, — и даже больше. Листочки ваш партнер раскладывает на столе так, чтобы написанные на них числа были обращены вниз, и вы начинаете по очереди переворачивать их. Дойдя до числа, которое, по вашему мнению, является наибольшим из написанных, вы останавливаетесь. Возвращаться и выбирать числа на уже перевернутых листочках не разрешается.

Если вы перевернули все листочки, то выбрать можете только то число, которое стоит на самом последнем листке.

По мнению большинства, имеется по крайней мере пять шансов против одного, что вы не сможете указать наибольшее число. На самом деле, если вы будете придерживаться оптимальной стратегии, ваши шансы окажутся немного выше одной трети. Возникает два вопроса. Во-первых, в чем состоит оптимальная стратегия?

(Заметим, что она не совпадает со стратегией, стремящейся максимизировать значение выбранного числа.) Во-вторых, если придерживаться оптимальной стратегии, то как подсчитать вероятность выигрыша?

Если имеется только два листка бумаги, то вероятность выигрыша равна 1/2 независимо от того, какой листок вы выберете. С увеличением числа листков вероятность выигрыша (предполагается, что вы придерживаетесь оптимальной стратегии) убывает, но кривая быстро выходит на горизонтальную асимптоту и при числе листков, превышающем 10, изменяется очень мало. Вероятность выигрыша никогда не опускается ниже 1/3. Многие полагают, что, выбирая очень большие числа, они существенно усложняют задачу, однако, как показывает некоторое размышление, величина чисел не играет никакой роли. Необходимо только, чтобы числа на листках можно было расположить в порядке их возрастания.

Игра в гугол имеет много интересных применений. Вот, например, одно из них. Девушка решает выйти замуж до конца года.

Она надеется, что ей удастся встретить десять человек, которые сделают ей предложение (получив отказ, каждый из претендентов на ее руку не проявляет особой настойчивости и от дальнейших попыток добиться согласия своей избранницы отказывается). Какой стратегии следует ей придерживаться, чтобы увеличить свои шансы выбрать самого достойного из женихов? С какой вероятностью она добьется успеха?

Оптимальная стратегия состоит в том, чтобы, отвергнув некоторое число листков бумаги (или предложений), выбрать следующее число, которое превосходит наибольшее из отвергнутых чисел.

Требуется найти лишь формулу, которая бы показывала, сколько листков следует отбросить в зависимости от полного числа листков.

4. Марширующие курсанты и беспокойный терьер. Курсанты военного училища построены в каре (квадрат со стороной 15 м) и маршируют с постоянной скоростью (рис. 187).

 

Рис. 187 К задаче о марширующих курсантах и терьере.

Небольшой терьер, любимец роты, выбегает из середины последней шеренги (из точки А на рис. 187) и устремляется по прямой к середине первой шеренги (к точке В). Достигнув цели, он поворачивает и снова бежит по прямой к середине последний шеренги. К моменту его возвращения в точку А курсанты успевают пройти ровно 15 м.

Какое расстояние пробежал терьер, если предположить, что он двигается с постоянной скоростью, и пренебречь потерей времени при повороте?

Решив эту задачу, которая требует лишь знания элементарной алгебры, вы можете испытать свои силы в решении более сложного ее варианта, предложенного уже известным нам изобретателем головоломок Сэмом Лойдом. В этом варианте задачи щенок бегает не вперед и назад через строй марширующих курсантов, а с постоянной скоростью обегает по периметру квадрата (держась все время как можно ближе к своей роте). Как и в предыдущем случае, к моменту его возвращения в точку А курсанты успевают пройти 15 м.

Какое расстояние пробегает пес?

5. Пояс Барра. Стивен Барр поведал нам, что у его халата имеется длинный матерчатый пояс, концы которого срезаны под углом 45° (рис. 188).

 

Рис. 188 Пояс Барра и один из неправильных способов его укладки.

Готовясь к поездке, Барр сложил халат и хотел как можно туже скатать пояс, начав с одного конца, но косо срезанные концы оскорбляли свойственное ему чувство симметрии. Если он подворачивал уголок, чтобы конец пояса был прямым, то необычная толщина конца при скатывании пояса приводила к уродливым выступам и буграм. Барр пытался прибегнуть к более хитроумным способам, но безуспешно. Одна из таких неудачных попыток показана на рис. 188: на участке А пояс сложен втрое, а на участке В — всего лишь вдвое.

Все же Барру удалось в конце концов так сложить свой пояс, что каждый конец его был прямым, а весь пояс в сложенном состоянии имел форму прямоугольника и всюду одинаковую толщину, после чего его уже нетрудно было скатать в ровный, тугой рулон.

Как Барр сложил свой пояс? При решении задачи можно пользоваться длинной полоской бумаги, концы которой обрезаны под углом 45°.

6. Уайт, Блэк и Браун Профессор математического факультета Мерль Уайт, профессор философии Лесли Блэк и секретарь деканата Джин Браун завтракали за одним столом.

— Разве не удивительно, — заметила девушка, — что наши фамилии Блэк, Браун и Уайт и что у одного из нас волосы черные, у другого — каштановые, а у третьего — совсем белые?

— Действительно, забавно, — заметила особа с черными волосами. — А вы обратили внимание, что ни у одной из нас цвет волос не соответствует фамилии?

— Ей Богу, вы правы! — воскликнул (или воскликнула) профессор Уайт.

Какого цвета волосы у профессора Блэка, если цвет волос у девушки не каштановый?

7. Самолет и ветер. Самолет летит по прямой из аэропорта А в аэропорт В, а затем обратно из В в А снова по прямой. Он летит с постоянной скоростью, ветер отсутствует. Будет ли время в пути больше, меньше или останется таким же, если полет происходит по тому же маршруту, с той же скоростью, но на обоих отрезках пути дует с одинаковой скоростью ветер? Направление ветра — из А в В.

8. Сколько стоят обитатели зоомагазина? Владелец небольшого зоомагазина приобрел некоторое количество хомяков и вдвое меньшее количество пар длиннохвостых попугаев. За каждого хомяка он заплатил по два доллара, а за каждого попугая — по одному. При продаже он запрашивал за каждого из них цену на 10 % больше той, что платил сам.

Распродав всех хомяков и попугаев, кроме семи, владелец магазина обнаружил, что выручка от продажи в точности равна сумме, затраченной им на всю покупку. Следовательно, его потенциальная прибыль равна общей цене оставшихся семи хомяков и попугаев.

Сколько стоит оставшаяся живность?

Ответы

1. Разрезать тупоугольный треугольник на остроугольные можно всегда. Схема разрезания на семь остроугольных треугольников, применимая к любому тупоугольному треугольнику, показана на рис. 189.

 

Рис. 189 Тупоугольный треугольник, разрезанный на семь остроугольных треугольников.

Нетрудно видеть, что число семь минимально. Тупой угол должен быть разрезан по какой-то прямой. Эта прямая не может доходить до противолежащей стороны, ибо тогда получился бы другой тупоугольный треугольник, который в свою очередь нужно было бы разрезать, вследствие чего схема разрезания большого треугольника не была бы минимальной. Поэтому линия, по которой разрезают тупой угол, должна заканчиваться в некоторой точке внутри треугольника. В этой точке должны сходиться по крайней мере пять линий разреза, в противном случае не все углы при этой вершине были бы острыми. Отсюда получается внутренний пятиугольник из пяти остроугольных треугольников, а общее число остроугольных треугольников становится равным семи.

Возникает вопрос: можно ли произвольный тупоугольный треугольник разрезать на семь остроугольных равнобедренных треугольников? Оказывается, этого сделать нельзя? А вот прямоугольный и остроугольный треугольники (каждый из них в отдельности) можно разрезать на девять остроугольных равнобедренных треугольников, а остроугольный равнобедренный треугольник можно разрезать на четыре одинаковых равнобедренных треугольника, подобных исходному.

Квадрат можно разрезать на восемь остроугольных треугольников так, как показано на рис. 190.

 

Рис. 190 Квадрат, разрезанный на восемь остроугольных треугольников.

Если линии разрезов симметричны относительно вертикальной оси квадрата, то точки Р и Р' должны лежать внутри заштрихованной области, граница которой образована дугами четырех полуокружностей. Возможно и асимметричное расположение линий разрезов, при котором точка Р выходит за пределы заштрихованной области, но остается внутри двух больших полукругов.

Г. С. М. Коксетер обратил внимание на удивительный факт: для любого прямоугольника, как бы мало ни отличались по длине его стороны, отрезок РР' всегда можно переместить в центр квадрата, так что линии разрезов будут симметричны не только относительно вертикальной, но и относительно горизонтальной оси.

Нельзя не упомянуть и два нерешенных вопроса. Квадрат можно разрезать на одиннадцать равнобедренных остроугольных треугольников. Минимально ли это число? Существует ли четырехугольник, который нельзя было бы разрезать на восемь или меньшее число остроугольных треугольников?

На рис. 191 показаны схемы разрезания пентаграммы (правильной пятиконечной звезды) и греческого креста на наименьшее из возможных число остроугольных треугольников.

 

Рис. 191 Пятиугольная звезда (пентаграмма) и греческий крест, разрезанные на минимальное число остроугольных треугольников.

2. Объем сферы равен кубу ее радиуса, умноженному на 4π/3.

Площадь поверхности сферы равна квадрату ее радиуса, умноженному на 4π. Выразив радиус Луны в лунарах и предположив, что ее поверхность в квадратных лунарах равна ее объему в кубических лунарах, мы сможем определить длину радиуса, если приравняем оба выражения и решим полученное уравнение относительно радиуса. Число π сокращается и в правой и в левой части, и мы получат ем, что радиус Луны равен трем лунарам. Поскольку радиус Луны равен 1738 км, один лунар равен 579 1/3 км.

3. Независимо от того, сколько листков бумаги берут играющие в гугол, вероятность выбрать листок с наибольшим числом никогда не опускается ниже 0,367879 (предполагается, что играющий придерживается оптимальной стратегии). Эта величина обратна числу е и служит пределом вероятности выигрыша, когда число листков стремится к бесконечности.

Если для игры взято десять листков (это число особенно удобно), то вероятность выбрать листок с наибольшим числом равна 0,398. Оптимальная стратегия состоит в том, чтобы, перевернув три листка, выбрать наибольшее из значащихся на них чисел, а затем продолжать переворачивать листки до тех пор, пока не встретится еще большее число. При достаточно продолжительной игре такая тактика гарантирует выигрыш в двух случаях из пяти возможных.

Анализ игры в гугол сводится к следующему. Пусть π — число листков бумаги, взятых для игры, р — число листков, перевернутых до того, как было выбрано число, превосходящее любое из чисел, проставленных на этих листках. Перенумеруем листки по порядку от 1 до π. Пусть (k + 1) — номер листка с наибольшим числом. Для того чтобы мы могли выбрать наибольшее число, k должно быть не меньше р (в противном случае, при k < р, наибольшее число будет для нас безвозвратно «утеряно», так как окажется на одном из р первых листков), при этом наибольшее из чисел на листках от 1 до А; должно одновременно быть наибольшим из чисел от 1 до р (в противном случае мы бы не смогли дойти до наибольшего из всех чисел, так как остановили бы свой выбор на наибольшем из чисел, значащихся на листках с номерами от 1 до р). Вероятность найти наибольшее число, если оно выписано на (k + 1) — м листке, равна p/k, а вероятность того, что наибольшее число действительно стоит на (k+1) — м листке, равна 1/n. Поскольку наибольшее число может стоять только на одном листке, мы получаем для вероятности «накрытия» этого числа следующую формулу:

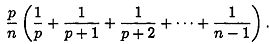
При заданном значении п (числа листков) формула позволяет находить оптимальное значение р (числа листков, которые нужно перевернуть) — то значение р, при котором выписанное выражение достигает максимума. При π, стремящемся к бесконечности, p/n стремится к 1/e, поэтому хорошим приближением для р можно считать ближайшее к n/e целое положительное число. Итак, при игре с п листками стратегия заключается в том, чтобы переворачивать листки до тех пор, пока их число не превысит n/e, а затем выбрать первое же число, большее максимального, из чисел, записанных на перевернутых n/e листках.

Разумеется, приведенное выше рассуждение исходит из предположения о том, что играющему не известны наибольшее и наименьшее из чисел, выписанных на листках, и поэтому, увидев очередное число, он не может судить о том, насколько близко оно к верхней или нижней границе того отрезка числовой оси, которой принадлежит выбранное число. Если играющий располагает такими сведениями, то все рассуждение становится неприменимым. Например, если вместо листков бумаги при игре в гугол взять десять долларовых купюр с их банковскими номерами, то, вытащив доллар, номер которого начинается с девятки, вам лучше всего объявить этот номер наибольшим. По аналогичным причинам игра в гугол, если говорить строго, неприменима и к задаче о девушке, жаждущей выйти замуж, ибо, как отметили многие читатели, девушка, по-видимому, великолепно осведомлена о достоинствах своих поклонников и подходит к ним с определенными мерками. Если первый же, кто делает ей предложение, очень близок к ее идеалу, то, как написал нам один из читателей, «она будет просто дурой, если не примет предложения».

Задача о максимизации значения выбранного объекта (а не вероятности выбора объекта с наибольшим значением), насколько известно, была впервые поставлена знаменитым математиком Артуром Кэли в 1875 году.