1. «Квадратобоязнь». В эту игру, которую мы для краткости будем называть KB Б, играют на шахматной доске размером 6x6 клеток.

Один игрок берет себе 18 белых фишек, другой — 18 черных. Каждый из игроков по очереди имеет право поставить одну фишку на любую свободную клетку доски, следя за тем, чтобы его фишки не оказались расположенными в вершинах квадрата. Квадрат может быть любого размера и наклонен под любым углом. Существует 105 различных способов построения квадратов; некоторые из них показаны на рис. 226.

 

Рис. 226 Четыре из 105 возможных квадратов при игре в «Квадратобоязнь».

Игрок одерживает победу, когда его противник вынужден построить один из 105 возможных квадратов. В КВБ можно играть на доске фишками или на листе бумаги с карандашом в руках. В последнем случае нужно начертить доску и отмечать ходы крестиками и ноликами.

В течение нескольких месяцев после того, как я придумал эту игру, меня не покидала уверенность в том, что KBБ не может закончиться вничью. Позднее Г. М. Мак-Лури, студент-математик из Оклахомского университета, доказал, что ничья все-таки возможна.

Разделив 36 клеток на две группы по 18 клеток в каждой так, чтобы никакие четыре клетки, входящие в одну и ту же группу, не образовывали вершин квадрата, попробуйте показать, каким образом игра в КВБ может закончиться вничью.

2. Головоломка с маневровым тепловозом. Составление железнодорожных составов нередко приводит к трудным задачам из области исследования операций. Задача с маневровым тепловозом, изображенная на рис. 227, обладает тем достоинством, что сочетает в себе простоту формулировки с удивительной трудностью решения.

 

Рис. 227 Головоломка из области исследования операций.

Тоннель достаточно широк для того, чтобы через него свободно проходил тепловоз, но узок для вагонов. Задача состоит в том, чтобы, пользуясь тепловозом, поменять местами верхний и нижний вагоны и вернуть тепловоз в исходное положение. Тепловоз может тянуть и толкать вагоны спереди и сзади. Вагоны, если это необходимо, можно сцеплять друг с другом.

Лучшим считается решение, при котором требуемый результат достигается наименьшим числом операций. Под «операцией» здесь понимается любой пробег тепловоза между двумя остановками (останавливается тепловоз перед тем, как начать двигаться в обратном направлении, при подходе к вагону, который нужно толкнуть, или когда от него отцепляют вагон, который до того он тянул за собой). Перевод стрелок операцией не считается.

При решении задачи удобно пользоваться наглядной «моделью»: положив на рисунок три монеты различного достоинства, передвигать их по рельсам. Не нужно лишь забывать, что через тоннель может проходить только монетка, изображающая тепловоз. На рис. 227 вагон стоит слишком близко от стрелок. При решении задачи можно считать, что оба вагона расположены намного дальше «к востоку» и на отрезке пути, отделяющем их от стрелок, может разместиться тепловоз с другим вагоном.

Переводить стрелки «на ходу» не разрешается. Например, нельзя переводить стрелку в тот момент, когда тепловоз только протолкнул через нее не сцепленный с ним вагон, чтобы вагон покатился по одной ветке, а тепловоз, не останавливаясь, продолжал движение по другой.

3. Рекламные щиты на шоссе. Смит мчался на машине по шоссе с постоянной скоростью. Рядом с ним в кабине сидела его жена.

— Ты заметила, — обратился он к ней, — что эти надоедливые щиты с рекламой пива расставлены на одинаковом расстоянии друг от друга? Хотелось бы знать, на каком именно.

Миссис Смит посмотрела на часы и сосчитала, сколько рекламных щитов промелькнуло за окном в течение одной минуты.

— Какое странное совпадение! — воскликнул Смит. — Если это число умножить на 10, то получится в точности скорость нашей машины в милях в час.

Предположим, что скорость машины постоянна, щиты расставлены через правильные промежутки, а минута, отмеренная миссис Смит, начинается и кончается в моменты, когда машина находится как раз посреди расстояния, отделяющего один рекламный щит от другого. Спрашивается, чему равно это расстояние?

4. Как разрезать кубик и как разрезать бублик. Инженер, известный своей склонностью к геометрическим построениям, как-то раз пил кофе с бубликом. Прежде чем бросить в чашку кусочек сахара, имевший форму кубика, он положил его на стол и подумал: «Если я проведу горизонтальную плоскость через центр куба, то в сечении, разумеется, получится квадрат. Если я проведу плоскость через центр куба и четыре его вершины, то в сечении получится вытянутый прямоугольник. Если же я проведу плоскость вот так, то…».

К своему удивлению, инженер, мысленно представив себе форму сечения, ясно увидел, что оно имеет форму правильного шестиугольника.

Каким образом он провел секущую плоскость? Если длина ребра куба равна 0,5 дюйма, то чему равна сторона правильного шестиугольника?

Бросив кубик сахару в кофе, инженер обратил внимание на бублик, лежавший перед ним на тарелочке.

«Если я проведу через центр бублика горизонтальную плоскость, то в сечении получатся две концентрические окружности, — сказал он себе. — Если я проведу вертикальную плоскость, проходящую через центр бублика, то в сечении получатся две окружности, отстоящие друг от друга на расстояние, равное ширине дырки бублика. Если же я проведу плоскость вот так, то…». От удивления он даже присвистнул: сечение имело вид двух пересекающихся окружностей!

Как было проведено последнее сечение? Если бублик имеет форму идеального тора, наружный диаметр которого равен 3 дюймам, а дырка имеет поперечник в 1 дюйм, то чему равны диаметры пересекающихся окружностей?

5. Как разделить пополам инь и ян? Два математика зашли пообедать в китайский ресторан «Инь и ян», расположенный на одной из улиц Манхэттена. Дожидаясь, когда их обслужат, они заговорили о символе, изображенном на карточке меню (рис. 228).

 

Рис. 228 Монада. Начало инь окрашено в черный цвет, а противоположное ему начало ян — в белый.

— Я думаю, это один из древнейших религиозных символов мира, — сказал один из них. — Вряд ли можно более наглядно и изящно изобразить противоположные начала, действующие в природе: добро и зло, мужчину и женщину, инфляцию и дефляцию, интегрирование и дифференцирование.

— Но этот же символ служит и фирменным знаком Северной Тихоокеанской железной дороги?

— Да. Я знаю, что один из главных инженеров компании видел эту эмблему на корейском флаге во время Чикагской всемирной выставки в 1893 году и уговорил правление сделать ее фирменным знаком. Он считал, что эта эмблема символизирует противоположность огня и воды, приводящих в движение паровоз.

— А как ты думаешь, не вдохновил ли этот древний китайский символ создателей современного бейсбольного мяча?

— Я бы не удивился, если бы узнал, что дело обстоит именно так. Кстати, ты знаешь, что существует изящный метод, позволяющий одной прямой разделить оба символа — инь и ян — на две равновеликие (по площади) части?

Предположим, что граница между символами инь и ян образована двумя полуокружностями. Как в этом случае одновременно разделить оба символа одной и той же прямой на две равные по площади части?

6. Голубоглазые сестры. Если вы случайно встретите двух сестер Джонс (это означает, что каждая из встреченных вами сестер случайным образом выбрана из множества всех сестер Джонс), то в 50 % всех случаев окажется, что обе сестры голубоглазые. Каково, по вашему мнению, общее число голубоглазых девушек среди сестер Джонс?

7. Город, как роза, красный и его возраст. Два профессора (один — английской литературы, другой — математик) встретились в баре факультетского клуба.

— Интересно, — заметил профессор, читавший курс английской литературы, — что некоторым поэтам удается написать лишь одну бессмертную строку. Все остальное в их творчестве не имеет непреходящего значения. Взять, например, Джона Уильяма Бергона.

Его поэмы настолько посредственны, что сейчас их никто не читает, а ведь именно он написал одни из самых замечательных строк в английской поэзии:

Математик, любивший надоедать своим друзьям импровизированными головоломками, задумался на минуту, затем поднял бокал и прочитал следующие стихи:

Профессор английской литературы давным-давно забыл все, чему его учили в школе на уроках алгебры, поэтому он быстро перевел разговор на другую тему, но для нашего читателя решение задачи не составит никакого труда.

8. Хитроумное состязание. Три колледжа — Вашингтона, Линкольна и Рузвельта—решили провести легкоатлетический матч. В каждом из видов спорта от каждого колледжа выступал один и только один участник.

Сьюзен, студентка колледжа Линкольна, сидела на трибуне и подбадривала своего приятеля, чемпиона колледжа по толканию ядра. Когда она вернулась домой, отец спросил у нее, как выступали спортсмены ее колледжа.

— Мы заняли первое место по толканию ядра, — сказала она, — но матч выиграл колледж Вашингтона. Они набрали 22 очка. Мы и колледж Рузвельта получили лишь по 9 очков.

— А как начислялись очки? — спросил отец.

— Точно не помню, — ответила Сьюзен, — но победитель в каждом виде легкой атлетики получал определенное количество очков, занявший второе место получал меньшее количество очков, а вышедший на третье место получал еще меньше очков. Число очков за каждое место во всех видах присуждалось одинаковое. (Под «числом очков» Сьюзен, конечно, имела в виду целое положительное число.)

— А по скольким видам спорта проводились соревнования?

— Честное слово, не помню, папа. Я все время смотрела толкание ядра.

— А прыжки в высоту были? — спросил брат Сьюзен.

Сьюзен кивнула.

— А кто выиграл прыжки?

Этого Сьюзен не знала.

Как ни странно, но на последний вопрос можно ответить, располагая лишь теми сведениями, которые мы уже имеем. Итак, какой колледж выиграл соревнования по прыжкам в высоту?

9. Термит и 27 кубиков. Представим себе большой куб, склеенный из 27 меньших деревянных кубиков одинакового размера (рис. 229).

 

Рис. 229 К задаче о термите и кубиках.

Термит садится на центр грани одного из наружных кубиков и прогрызает ход, пронизывающий все кубики. Побывав в одном кубике, термит уже больше к нему не возвращается. Двигается он при этом всегда параллельно какому-нибудь ребру большого куба, но никогда—параллельно диагонали.

Может ли термит прогрызть все 26 внешних кубиков, побывав в каждом из них лишь по одному разу, и закончить свой ход в центральном кубике? Если это возможно, покажите, каким должен быть путь термита. Если же вы считаете, что это невозможно, докажите свое утверждение.

Предполагается, что после того, как термит прогрыз наружную грань самого первого кубика, его путь пролегает целиком внутри большого куба. В противном случае он мог бы выбраться на поверхность большого куба и переползти в начальную точку нового хода. При этом никакой задачи, разумеется, не возникло бы.

Ответы

1. На рис. 230 показана игра в КВБ, закончившаяся вничью. Это изящное решение, найденное Мак-Лури, очень непросто.

 

Рис. 230 Ничья при игре в КВБ.

Двое читателей, перебрав все возможные случаи, показали, что оно единственно с точностью до небольших вариаций в четырех клетках доски, указанных стрелками. Каждая из этих клеток может быть любого цвета, но все четыре клетки не должны быть одного и того же цвета, а поскольку каждый игрок имеет лишь восемнадцать фишек, то две из этих четырех клеток должны быть одного цвета, а две — другого. Расположены они так, что, как бы мы ни поворачивали доску, схема их размещения с точностью до цвета остается неизменной.

Доска размером 6x6 клеток — самая большая из досок, на которых возможна ничья. Это доказал в 1960 году Роберт А. Джьюитт.

Он сумел показать, что ничья невозможна на доске размером 7x7 клеток, а поскольку все большие доски содержат подквадрат из 7x7 клеток, то ничья на них также невозможна.

При игре в КВБ на доске размером 6x6 клеток всегда можно добиться ничьей. Следуя довольно простой симметричной стратегии, второй игрок всегда может свести игру вничью. Он может в ответ на каждый ход противника ставить свою фишку на поле, расположенное симметрично вертикальной или горизонтальной оси доски, или на поле, в которое переходит при повороте на 90° вокруг центра доски клетка, занятая последней фишкой противника (во втором случае может возникнуть позиция, изображенная на рис. 230). Возможна и другая стратегия: последнюю занятую противником клетку соединить с центром доски и, продолжив отрезок прямой по другую сторону от центра, занять клетку на этой прямой, отстоящую от середины доски на то же расстояние, что и клетка противника. Все стратегии применимы к любым доскам четного порядка, а поскольку на досках, порядок которых превышает 6, ничья невозможна, эти стратегии обеспечивают победу второму игроку на всех досках четного порядка, начиная с 8. Даже при игре на доске 6x6 зеркальносимметричная стратегия (когда второй игрок «отражает» ходы первого в оси, делящей доску пополам и параллельной ее краю) заведомо обеспечивает победу, поскольку единственная позиция, при которой достигается ничья, не обладает зеркальной симметрией.

Симметричная стратегия неприменима к доскам нечетного порядка из-за наличия у них центральной клетки. Поскольку относительно оптимальной стратегии для игры на досках нечетного порядка мы ничего не знаем, лучше всего ограничиваться доской седьмого порядка. Игра на такой доске не может закончиться вничью, но до сих пор не известно, кто из игроков — первый или второй — одержит победу, если обе стороны будут играть рационально.

В 1963 году была составлена программа для игры в КВБ для компьютера ИБМ-1620. Компьютер мог играть, делая первый или второй ход, на досках порядка от 4 до 10. Если он должен был делать первый ход, то выбирал клетку случайным образом. В последующих ходах придерживался зеркальносимметричнои стратегии, но если очередная клетка «достраивала» квадрат (то есть была четвертой вершиной квадрата), то производил случайный поиск свободной клетки до тех пор, пока не обнаруживал «безопасного» поля.

Для всех квадратных досок порядка п число различных квадратов, которые можно построить из четырех клеток, равно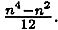

Вывод этой формулы, а также формулы для прямоугольных досок содержится в книге Г. Лэнгмэна «Математика в играх».

Насколько известно, возможность размещения фишек, не образующих треугольников, на треугольных досках не исследовалась.

2. Тепловоз может переставить вагоны А и В и вернуться на прежнее место за шестнадцать операций:

1) тепловоз едет вправо и сцепляется с вагоном А;

2) тащит А вниз;

3) заталкивает А на левую ветку и отцепляется от него;

4) движется вправо и проходит стрелку;

5) двигаясь по часовой стрелке, описывает круг и проходит тоннель;

6) толкает вагон В влево; оба вагона прицепляют к тепловозу;

7) тащит вагоны А и В вправо;

8) заталкивает А и В наверх; вагон А отцепляют от В;

9) тепловоз тащит В вниз;

10) толкает В влево, вагон В отцепляют от тепловоза;

11) тепловоз проходит сквозь тоннель, описывая круг против часовой стрелки;

12) заталкивает вагон А вниз;

13) едет влево и сцепляется с В;

14) тащит вагон В вправо;

15) заталкивает В наверх и отцепляется от него;

16) уезжает влево, на то место, где находился до начала маневров.

Точно так же можно действовать и в том случае, когда тепловоз не может тащить вагоны, прицепленные к нему спереди, если в самом начале тепловоз обращен к вагонам задней стенкой.

Следует заметить, что если даже нижний путь, ведущий влево, убрать, то задача все же будет иметь решение, хотя понадобится совершить еще две операции (полное решение будет, таким образом, состоять из восемнадцати операций). Может быть, читатели сами догадаются, как это сделать?

3. Самое интересное в задаче о рекламных щитах заключается в том, что для ответа на нее не нужно знать скорость машины. Пусть х — число щитов, промелькнувших в течение одной минуты. За час машина проедет мимо 60х щитов. Скорость машины, как известно из условия задачи, равна 10х миль/ч. Пройдя расстояние в 10х миль, машина проедет мимо 60х рекламных щитов, следовательно, на расстоянии 1 мили она проедет мимо 60х/10х, или 6 щитов. Это означает, что расстояние между щитами равно 1/6 мили, или 880 футам.

4. Если куб разрезать пополам плоскостью, проходящей через середины шести его ребер так, как показано на рис. 231, то поперечное сечение будет иметь вид правильного шестиугольника.

 

Рис. 231 Сечение куба, имеющее форму правильного шестиугольника.

Если длина ребра куба составляет полдюйма, то сторона этого правильного шестиугольника равна

дюйма.

Чтобы сечение тора имело вид двух пересекающихся окружностей, секущая плоскость должна проходить через его центр и касаться тора сверху и снизу (рис. 232).

 

Рис. 232 Ответ к задаче о разрезании бублика.

Если диаметры тора и отверстия равны трем и одному дюйму, то диаметр каждой окружности в поперечном сечении равен, очевидно, двум дюймам.

Этим способом разрезания тора вместе с двумя другими способами, упоминавшимися в условии задачи, исчерпываются все случаи, когда сечение тора плоскостью имеет вид так или иначе расположенных окружностей.

5. На рис. 233 показано, как провести прямую, которая делит инь и ян на две равные по площади части. Проще всего это сделать, если провести две пунктирные полуокружности. Диаметр круга К равен половине диаметра монады, поэтому его площадь составляет 1/4 площади монады (напомним, что монадой называется круг, образованный двумя противоположными началами инь и ян). Вырезав из круга К лунку G и добавив область Н, получим фигуру, площадь которой по-прежнему будет в четыре раза меньше площади всей монады. Отсюда следует, что площадь G равна площади Н, а половина площади G равна половине площади Н. Проведенная прямая отсекает от круга К половину лунки G, но добавляет к К фигуру равной площади (половину Н), поэтому та часть монады, которая лежит ниже прямой и окрашена в черный цвет, должна занимать ту же площадь, что и круг К. Площадь маленького круга в четыре раза меньше площади большого круга, поэтому инь делится прямой пополам. Аналогичные рассуждения применимы и к ян.

Предыдущее доказательство принадлежит Г. Дьюдени. Однако существует другое, гораздо более простое доказательство. На рис. 233 проведем горизонтальный диаметр малого круга К.

 

Рис. 233 Как одной прямой разделить пополам инь и ян.

Полукруг, лежащий под этим диаметром, очевидно, имеет площадь, составляющую 1/8 площади всей монады. Над проведенным диаметром располагается сектор большого круга в 45° (ограниченный горизонтальным диаметром малого круга К и диагональю квадрата, в который вписана монада). Его площадь, очевидно, также составляет 1/8 площади большого круга. Взятые вместе, полукруг и сектор имеют площадь, равную 1/4 площади большого круга, поэтому проведенная диагональная линия должна делить и инь и ян пополам.

Способы деления инь и ян на две равные по площади части кривыми линиями читатель найдет в статье Тригга «Деление инь и ян пополам».

Обычно символ инь — ян (называемый Цай-чи-цю в Китае и Томойе в Японии) рисуют так, что оба начала чуть-чуть находят друг на друга. Это символизирует то обстоятельство, что в жизни противоположности редко встречаются в чистом виде и обычно в одной из противоположностей имеется легкая примесь другой. Символу инь—ян посвящена обширная восточная литература. Сэм Лойд, положивший этот символ в основу нескольких головоломок, называл его Великой Монадой. Термин «монада» повторяет Дьюдени; этот же термин использует в небольшой книжке «Страна чудес», выпущенной в 1901 году Северной Тихоокеанской железнодорожной компанией, Олин Д. Уилер. Первая глава книжки Уилера посвящена истории эмблемы железнодорожной компании и содержит любопытные сведения и цветные репродукции восточных источников. Более подробно о символе инь — ян можно прочитать в статье Шуйлера Каммана «Магические квадраты третьего порядка в древнекитайской философии и религии», в моей книге «Этот правый, левый мир» и в первом томе книги Дж. Сартона «История науки». Существует книга «Китайская монада, ее история и значение», написанная Вильгельмом фон Гогенцоллерном, но я не знаю ни даты ее выпуска, ни фамилии издателя.

6. По всей видимости, в семье Джонсов имеются четыре сестры и у троих из них голубые глаза. Если имеется n девушек и у Ь из них глаза голубого цвета, то вероятность того, что выбранные случайным образом две девушки будут голубоглазыми, равна

Мы знаем, что в нашем случае эта вероятность равна 1/2, поэтому задача сводится к отысканию таких целочисленных значений Ь и n, при которых выписанное выражение имеет значение 1/2. Наименьшими из таких значений являются n = 4 и Ь = 3. Ближайшие по величине значения составляют n = 21, b = 15, но, поскольку крайне невероятно, чтобы в одной семье была 21 сестра, мы будем считать ответом первую пару значений: четыре сестры, из которых три — голубоглазые.

7. Возраст «как роза, красного» города составляет семь миллиардов лет. Пусть х — возраст города, у — возраст вечности (в миллиардах лет). Миллиард лет назад возраст города составлял х — 1, а возраст вечности через миллиард лет составит у + 1 миллиардов лет. Условия задачи позволяют записать два простых уравнения:

 

Из этих уравнений мы находим х — возраст города; оказывается, х = 7000000000 лет, а у — возраст, достигнутый вечностью, равен 14 миллиардам лет. Сама постановка задачи предполагает, таким образом, теорию образования Вселенной в результате Большого взрыва.

8. Из-за ограниченности места мы лишь наметим способ, пользуясь которым можно показать, что соревнования по прыжкам в высоту на легкоатлетическом матче трех колледжей выиграл колледж Вашингтона.

За первое, второе и третье места в каждом виде соревнований присуждалось различное (но непременно целое и положительное) число очков. За первое место победившая команда не может получить меньше 3 очков. В то же время мы знаем, что соревнования проводились по крайней мере по двум видам легкой атлетики (толканию ядра и прыжкам в высоту) и что колледж Линкольна (выигравший соревнование по толканию ядра) набрал 9 очков, поэтому число очков, присуждаемых за первое место, не может быть меньше 8. Может ли оно быть равным 8? Нет, потому что это означало бы, что соревнования проводились только по толканию ядра и прыжкам в высоту и колледж Вашингтона не мог бы набрать 22 очка. Число очков, присуждаемых за первое место, не может быть равным и 7, потому что в этом случае соревнования могли бы проводиться не более чем по трем видам легкой атлетики, а трех видов недостаточно для того, чтобы колледж Вашингтона набрал 22 очка. Несколько более сложными рассуждениями можно показать, что число очков, присуждаемое за первое место, не равно 6, 4 и 3. Единственной возможностью остается число 5.

Если команда, занявшая первое место получает 5 очков, то соревнования должны проводиться по крайней мере по пяти видам спорта (при меньшем числе видов колледж Вашингтона не наберет 22 очка, при большем — колледж Линкольна наберет больше 9 очков). Колледж Линкольна получает 5 очков за толкание ядра и, следовательно, по 1 за участие в соревнованиях по четырем другим видам спорта. Колледж Вашингтона может набрать 22 очка в двух случаях: получив 4, 5, 5, 5, 3 очка и получив 2, 5, 5, 5, 5 очков. Первая возможность исключается потому, что тогда колледж Рузвельта набрал бы 17 очков, а мы знаем, что его команда набрала всего лишь 9 очков. Оставшаяся возможность приводит к правильному числу очков у колледжа Рузвельта, и, таким образом, число очков, полученных каждой командой, восстанавливается однозначно (см. таблицу).

 

Колледж Вашингтона выигрывает соревнования по всем видам спорта, кроме толкания ядра, следовательно, он должен занять первое место и по прыжками в высоту.

Предположение о единственности ответа на задачу позволяет намного сократить решение. Вот что написала по этому поводу одна из читательниц:

9. Термит не может прогрызть 26 наружных кубов и закончить свое путешествие в центральном кубике. Это легко доказать, если представить, что кубики окрашены в шахматном порядке в какие-нибудь два цвета (они расположены, как ячейки в трехмерной шахматной доске или атомы хлора и натрия в кубической кристаллической решетке поваренной соли). Большой куб будет состоять из 13 кубиков одного и 14 кубиков другого цвета. Цвета кубиков на пути термита должны правильно чередоваться. Когда термит прогрызет все 27 кубиков, то начало и конец проделанного им хода должны принадлежать двум из 14 кубиков. Центральный же кубик принадлежит другому набору — из 13 кубиков. Следовательно, решения задачи не существует.

Задача допускает обобщение. Куб четного порядка (то есть склеенный из четного числа кубиков) состоит из одинакового числа кубиков каждого из двух цветов. Центрального кубика нет. Путь термита может начинаться с любого кубика одного цвета и заканчиваться в любом кубике другого цвета. У куба нечетного порядка маленьких кубиков одного цвета на один больше, чем кубиков другого, поэтому путь термита должен начинаться и заканчиваться на кубиках из большего набора. В кубах нечетного порядка 3, 7, 11, 15, 19… центральные кубики принадлежат меньшему набору, и проделанный термитом ход не может заканчиваться в них. У кубов нечетного порядка 1, 5, 9,13,17… центральные кубики принадлежат к большему набору, и в этих случаях ничто не мешает термиту закончить свой путь в самом центре большого куба, разумеется, при условии, что путь начинался в одном из кубиков того же цвета, что и центральный. В кубах нечетного порядка замкнутых ходов быть не может, потому что в них кубиков одного цвета на один больше, чем кубиков другого.

Многие двумерные головоломки также можно решать с помощью аналогичных «проверок на четность». Например, так можно доказать, что ладья не может перейти из одного угла шахматной доски в противоположный угол (по диагонали), побывав по одному разу на всех 64 клетках.