Зачёт № 1
Глава I. ВЫРАЖЕНИЯ, ТОЖДЕСТВА,
УРАВНЕНИЯ
(сентябрь, октябрь)
П.1. Вопросы:
- Что называют числовым выражением?
- Что называют значением выражения?
- О каких выражениях говорят, что они не имеют
смысла?
П.2. Вопросы:
- Что называют переменной (выражением с
переменной)?
- Что называют значением выражения с переменной?
- Назовите формулу чётного числа (нечётного
числа).
П.3. Вопросы:
- Какие неравенства называют строгими
(нестрогими)?
П.4. Вопросы:
- Сформулируйте переместительное и
сочетательное свойства сложения и умножения,
распределительное свойство умножения.
П.5. Вопросы:
- Какие выражения называют тождественно равными?
- Какое равенство называют тождеством?
П.6. Вопросы:
- Что называют преобразованием выражения?
- Перечислите правила выполнения тождественных
преобразований.
П.7. Вопросы:
- Что называют решением уравнения или корнем
уравнения?
- Что значит решить уравнение?
- Какие уравнения называют равносильными?
- Сформулируйте свойства уравнений.
П.8. Вопросы:
- Дайте определение линейного уравнения с одной
переменной.
- В каком случае уравнение ах = b имеет
единственный корень (не имеет корней, имеет
бесконечно много корней)?
П.9. Вопросы:
- Сформулируйте алгоритм решения задачи с
помощью уравнения.
Глава II. ФУНКЦИИ
(октябрь, ноябрь)
П.10. Вопросы:
- Что называют функцией?
- Что называют областью определения функции
(значениями функции)?
- Перечислите способы задания функции.
П.11. Вопросы:
- В каком случае считают, что область определения
функции состоит из всех значений независимой
переменной?
- Как решают задачу отыскания значений аргумента
(значений функции) с помощью формулы, задающей
функцию?
П.12. Вопросы:
- Сформулируйте определение линейной функции.
- Что называют графиком функции?
П.13. Вопросы:
- Какую функцию называют линейной?
- Что является графиком линейной функции?
- Как построить график линейной функции?
- Как определить, не выполняя построения,
проходит график функции через точку или нет?
Сформулируйте вопрос иначе.П.14.Вопросы:
Сформулируйте определение функции прямой
пропорциональности.
- Что является графиком? Как построить?
- Как расположен в координатной плоскости график
функции (k)?
П.15. Вопросы:
- В каком случае графики линейных функций
пересекаются?
- Как найти координаты точки пересечения?
- При каком условии графики линейных функций
параллельны?
Зачёт № 2
Глава III. СТЕПЕНЬ С НАТУРАЛЬНЫМ
ПОКАЗАТЕЛЕМ
(ноябрь, декабрь)
П.16. Вопросы:
- Сформулируйте определение степени с
натуральным показателем.
- Что называют основанием (показателем) степени?
- Что получается при возведении в степень
положительного числа?
- При возведении в степень нуля? Отрицательного
числа в чётную степень?
- Отрицательного числа в нечётную степень?
П.17. Вопросы:
- Сформулируйте и докажите основное свойство
степени.
- Сформулируйте правило деления степеней с
одинаковыми основаниями.
- Дайте определение степени числа с нулевым
показателем.
П.18. Вопросы:
- Сформулируйте правило возведения в степень
произведения, степени.
П.19. Вопросы:
- Какое выражение называют одночленом?
- Какой вид одночлена называют стандартным?
- Что называют степенью одночлена? Коэффициентом
одночлена?
П.20. Вопросы:
- Сформулируйте правила умножения (возведения в
степень) одночленов.
П.21. Вопросы:
- Перечислите свойства квадратичной функции. Как
отражаются эти свойства на графике функции?
- Перечислите свойства кубической функции. Как
отражаются эти свойства на графике функции?
- Как называются графики функций?
П.22. Вопросы:
- Что называют абсолютной погрешностью
приближённого значения?
П.23. Вопросы:
- Что называют относительной погрешностью
приближённого значения?
- В чём принято выражать относительную
погрешность?
Глава IV. МНОГОЧЛЕНЫ
(январь, февраль)
П.24. Вопросы:
- Дайте определение многочлена (двучлена,
трёхчлена).
- Какие слагаемые называют подобными членами
многочлена?
- Какие многочлены называют многочленами
стандартного вида?
- Что называют степенью многочлена?
П.25. Вопросы:
- Объясните, как складывают (вычитают) многочлены.
- Объясните, как представить многочлен в виде
суммы или разности многочленов.
П.26. Вопросы:
- Сформулируйте правило умножения одночлена на
многочлен.
- Сколько должно получиться одночленов в
результате умножения?
П.27. Вопросы: Какое преобразование называют
разложением многочлена на множители?
- Объясните способ разложения на множители с
помощью вынесения общего множителя за скобки.
П.28. Вопросы:
- Сформулируйте правило умножения многочлена на
многочлен.
- Сколько должно получиться членов при умножении
многочлена, содержащего k членов, на многочлен,
содержащий p членов?
П.29. Вопросы:
- Объясните, как выполняется разложение
многочлена на множители способом группировки.
Приведите пример.
П.30. Вопросы:
- Какое равенство называют тождеством?
- Как доказывают тождества?
Зачёт № 3
Глава V. ФОРМУЛЫ СОКРАЩЁННОГО
УМНОЖЕНИЯ
(февраль, март)
П.31. Вопросы:
- Назовите формулу квадрата суммы. Проведите
доказательство.
- Назовите формулу квадрата разности. Проведите
доказательство.
- Выведите формулу куба суммы (разности). (№ 885; №
886)
- Приведите примеры применения формул.
П.32. Вопросы:
- Что значит разложить на множители многочлен?
- Для разложения на множители выражений, какого
вида используют формулы квадрата суммы и
квадрата разности?
П.33. Вопросы:
- Чему равно произведение разности двух
выражений на их сумму?
- Как, используя это правило, найти значение
произведения: 52 x 48; 7,02 x 6,98; 25,3 x 24,7?
П.34. Вопросы:
- Какое тождество называют формулой разности
квадратов?
- Для чего применяют эту формулу?
П.35. Вопросы:
- Какое тождество называют формулой суммы
(разности) кубов?
- Проведите доказательство этих формул.
- Какой трёхчлен называют неполным квадратом
разности (суммы)?
П.36. Вопросы:
- Какие выражения называют целыми? Приведите
примеры.
- В каком виде можно представить любое целое
выражение?
П.37. Вопросы:
- Перечислите способы разложения многочлена на
множители.
- Опишите каждый из способов, приведите примеры.
П.38. Вопросы:
- Приведите примеры заданий, где применяются
преобразования целых выражений.
Зачёт № 4
Глава VI. СИСТЕМЫ ЛИНЕЙНЫХ
УРАВНЕНИЙ
(апрель, май)
П.39. Вопросы:
- Какое равенство называют уравнением с двумя
переменными?
- Дайте определение линейного уравнения с двумя
переменными.
- Что называют решением этого уравнения?
Перечислите его свойства.
П.40. Вопросы:
- Что называют графиком уравнения с двумя
переменными?
- Что является графиком линейного уравнения с
двумя переменными?
- Приведите пример линейного уравнения, график
которого параллелен оси абсцисс (оси ординат).
П.41. Вопросы:
- Что называют решением системы уравнений с двумя
переменными?
- Что значит решить систему уравнений? Сколько
решений может иметь система двух линейных
уравнений с двумя переменными?
- Какой способ решения системы уравнений
называют графическим?
П.42. Вопросы:
- Как решают систему двух линейных уравнений с
двумя переменными способом подстановки? Какие
системы называют равносильными?
П.43. Вопросы:
- Как решают систему двух линейных уравнений с
двумя переменными способом сложения? Когда
решение сразу начинают с почленного сложения
уравнений?
- Каким образом можно проверить ответы,
полученные аналитическим способом при решении
системы линейных уравнений?
П.44. Вопросы:
- Как поступают при решении задачи с помощью
системы уравнений?
8 КЛАСС
Зачёт № 1
Глава I. РАЦИОНАЛЬНЫЕ ДРОБИ
(сентябрь, октябрь)
П.1. Вопросы:
- Какие выражения называют целыми (дробными)?
Приведите примеры.
- Дайте определение рациональных выражений.
- Какие значения называют допустимыми значениями
переменных?
- О каких выражениях говорят, что они не имеют
смысла?
- Какую дробь называют рациональной? Приведите
примеры.
П.2. Вопросы:
- Какое равенство называют тождеством? Приведите
примеры.
- Какие выражения называют тождественно равными?
- Что называют тождественным преобразованием
выражения?
- Сформулируйте и докажите основное свойство
дроби.
- Сформулируйте правило об изменении знака перед
дробью.
П.3. Вопросы:
- Сформулируйте правило сложения (вычитания)
дробей с одинаковыми знаменателями. Приведите
примеры.
П.4. Вопросы:
- Сформулируйте правило сложения (вычитания)
дробей с разными знаменателями.
- Какие множители составляют наиболее простой
общий знаменатель дробей, которые складывают
(вычитают)?
П.5. Вопросы:
- Как умножают рациональные дроби? Приведите
примеры.
- Сформулируйте и докажите правило возведения
дроби в степень.
П.6. Вопросы:
- Сформулируйте правило деления рациональных
дробей.
П.7. Вопросы:
- Что называют преобразованием рациональных
выражений?
- Что должно получиться в результате
преобразования рационального выражения, если
указано, что его значение не зависит от значений
входящих в него в него переменных?
П.8. Вопросы:
- Какую функцию называют обратной
пропорциональностью?
- Какое множество чисел является её областью
определения?
- Как называется её график? Сколько точек
необходимо для построения?
- В каких координатных четвертях может быть
расположена гипербола (в зависимости от k).
Зачёт № 2
Глава II. КВАДРАТНЫЕ КОРНИ
(ноябрь, декабрь)
П.9. Вопросы:
- Какие числа образуют множество рациональных
чисел (натуральных, целых)? Какой буквой
обозначают каждое множество?
- От какого латинского слова произошёл термин
"рациональное число” и что оно означает?
- Как может быть представлено каждое
рациональное число?
- Какие десятичные дроби называют периодическими
(непериодическими)?
- Что называют периодом дроби? Как записывают
периодические дроби?
П.10. Вопросы:
- Какие числа называют иррациональными?
Приведите примеры.
- Какие числа образуют множество действительных
чисел?
- Какой буквой обозначают множество
действительных чисел?
- Какие действительные числа можно (какие нельзя)
представить в виде отношения целого числа к
натуральному числу?
П.11.Вопросы:
- Сформулируйте определение арифметического
квадратного корня.
- Как его записывают и при каких значениях он
имеет смысл?
П.12. Вопросы:
- Сколько корней имеет квадратное уравнение х2
= а (в зависимости от a)?
П.13. Вопросы:
- Как можно находить приближённые значения
арифметического квадратного корня?
- Каково приближённое значение
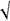 2 ( 2 (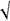 3 )? 3 )?
П.14. Вопросы:
- Какова область определения функции y =
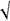 x? x? - Как расположен её график в системе координат?
- Что значит, что график функции проходит через
точку? Сформулируйте этот вопрос иначе.
П.15. Вопросы:
- Чему равен квадратный корень из произведения?
- Чему равен квадратный корень из дроби?
П.16. Вопросы:
- Чему равен квадратный корень из степени?
- Какое тождество применяют при извлечении
квадратного корня из степени с чётным
показателем? Приведите примеры.
- Перечислите свойства степеней с натуральными
показателями (повторение).
П.17. Вопросы:
- Объясните на примере, как можно вынести
множитель из-под знака корня.
- Объясните на примере, как можно внести
множитель под знак корня.
П.18. Вопросы:
- Какие преобразования выполняют с
иррациональными выражениями?
- Объясните на примере, как можно освободиться от
иррациональности в знаменателе дроби. Какие
выражения называют сопряжёнными?
- Назовите способы разложения многочлена на
множители.(повторение)
Зачёт № 3
Глава III. КВАДРАТНЫЕ УРАВНЕНИЯ
(декабрь, январь, февраль)
П.19. Вопросы:
- Сформулируйте определение квадратного
уравнения.
- Как называют коэффициенты квадратного
уравнения?
- Какое уравнение называют неполным квадратным
уравнением?
- Приведите пример неполного квадратного
уравнения каждого из трёх видов и укажите способ
его решения.
- Сколько корней имеет неполное квадратное
уравнение каждого вида?
П.20. Вопросы: Какое уравнение называют
приведённым квадратным уравнением?
- Объясните на примере, как можно решить
квадратное уравнение выделением квадрата
двучлена?
П.21. Вопросы: Какое выражение называют
дискриминантом квадратного уравнения?
- От какого латинского слова происходит название
дискриминанта?
- Сколько корней может иметь квадратное
уравнение?
- Напишите формулу корней квадратного уравнения
(желательно вывод).
- Сформулируйте алгоритм решения квадратного
уравнения по формуле.
- Напишите формулу корней квадратного уравнения,
в котором второй коэффициент является чётным
числом.
П.22. Вопросы:
- Сформулируйте алгоритм решения задач с помощью
квадратных уравнений.
П.23. Вопросы:
- Сформулируйте и докажите теорему Виета.
- Чему равны сумма и произведение корней
произвольного квадратного уравнения?
- Сформулируйте и докажите теорему, обратную
теореме Виета.
- Назовите корни произвольного квадратного
уравнения, если его дискриминант положителен и
сумма коэффициентов равна нулю.
П.24. Вопросы:
- Какие уравнения называют рациональными?
Приведите примеры.
- Какие рациональные уравнения называют целыми
(дробными)?
- Сформулируйте алгоритм решения дробного
рационального уравнения.
П.25. Вопросы:
- Сформулируйте алгоритм решения задач с помощью
дробных рациональных уравнений.
- Приведите пример решения задачи на движение (на
работу).
П.26. Вопросы:
- Объясните на примере, как графически решить
рациональное уравнение.
- Перечислите известные вам элементарные
функции, изобразите график, укажите название
графика. (повторение)
Зачёт №4
Глава IV. НЕРАВЕНСТВА
(февраль, март)
П.27. Вопросы:
- Какое выражение называют неравенством?
- Что такое строгое (нестрогое) неравенство?
- Сформулируйте правила сравнения обыкновенных
дробей, десятичных дробей, отрицательных чисел.
(повторение)
- Сформулируйте общее определение сравнения
чисел.
- Как изображают числа на координатной прямой?
П.28. Вопросы:
- Перечислите свойства числовых неравенств и
следствия из них.
- Приведите примеры.
П.29. Вопросы:
- Сформулируйте правила сложения, вычитания,
умножения и деления
- числовых неравенств. Приведите
примеры.П.30.Вопросы: Изобразите на координатной
прямой числовые промежутки различного вида и
запишите их обозначения.
- Какое множество называют пересечением
(объединением) других множеств? Как обозначают
эти множества? Приведите примеры.
П.31. Вопросы:
- Дайте определение линейного неравенства с
одной переменной.
- Приведите примеры линейных неравенств.
- Что называют решением неравенства с одной
переменной?
- Что значит решить неравенство?
- Какие неравенства называют равносильными?
- Перечислите свойства равносильности, которые
используют при решении неравенств.
- Приведите примеры неравенств, которые либо не
имеют решений, либо их решением является любое
число.
П.32. Вопросы:
- Что называют решением системы неравенств?
- Что значит решить систему неравенств?
- Покажите на примере, как решают двойное
неравенство.
Зачёт №5
Глава V. СТЕПЕНЬ С ЦЕЛЫМ
ПОКАЗАТЕЛЕМ
(апрель, май)
П. 33. Вопросы:
- Сформулируйте определение степени, определение
степени с целым отрицательным показателем.
П.34. Вопросы:
- Сформулируйте и запишите свойства степени с
целым показателем (произведение степеней,
частное степеней, степень степени, степень
произведения, степень частного).
П.35. Вопросы:
- Какую запись числа называют его стандартным
видом?
- Что называется порядком числа? Приведите
примеры.
- Как определить по порядку числа велико оно или
мало?
П.36. Вопросы:
- Что означает запись х = а ± k?
- Какую цифру называют верной цифрой
приближённого значения?
П.37. Вопросы:
- Как округляют результат при сложении
(вычитании, умножении, делении) приближённых
значений?
|

