В статье описан опыт преподавания элементов теории комплексных чисел в профильных классах старшей школы. Современная математика, физика, информатика и другие дисциплины основаны на действиях с действительными числами, поэтому учащиеся только обзорно знакомятся с комплексными числами.

Актуальность данной темы заключается в вечном вопросе: нужно ли знать математику менеджеру, социологу, аудитору и другим представителям гуманитарных профессий? А если нужно, то в какой мере? Вопросы далеко не праздные: на практике при решении многих конкретных управленческих проблем часто берут верх неформализуемые факторы, а применение математических методов сводится к использованию лишь четырех действий арифметики, а мнимые числа вообще не учитываются ни в каких расчетах.

Однако, по словам Леонардо да Винчи, "никакое человеческое исследование не может называться настоящим знанием, если оно не прошло через математические доказательства". Поэтому математически грамотно при решении обычных квадратных уравнений, имеющих отрицательный дискриминант говорить и писать, что уравнение не имеет действительных корней. При этом учащиеся должны быть знакомы с мнимыми числами, и если требуется, то вычислить корни уравнения, являющиеся мнимыми числами. Знание расширяет наш кругозор, делает осмысленными наши действия, а в дальнейшей практической жизни - исследования.

Обратимся к истории и посмотрим, какие существовали теории чисел. Древнегреческие математики считали "настоящими" только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел.

В III веке Архимед разработал систему обозначения вплоть до такого громадного как 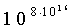. Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел - это было сделано китайскими математиками за два века до н. э.

Отрицательные числа применяли в III веке - древнегреческий математик Диофант, знавший уже правила действия над ними, а в VII веке эти числа уже подробно изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменения величин.

Уже в VIII веке было установлено, что уравнение 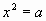при a>0 имеет два значения - положительное и отрицательное, а при a<0 не существует: нет такого числа x, чтобы .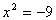

В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида 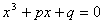кубические и квадратные корни:

Эта формула безотказно действует в случае, когда уравнение имеет один действительный корень

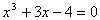а если оно имеет три действительных корня

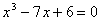то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени

нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).

В 1830 году Галуа (Франция) доказал, что никакое общее уравнение, степень которого больше чем 4, нельзя решить алгебраически. Тем не менее, всякое уравнение n-й степени имеет (если рассматривать и комплексные числа) n корней (среди которых могут быть и равные). В этом математики были убеждены еще в XVII веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже XVIII и XIX веков упомянутая теорема была доказана Гауссом.

Итальянский алгебраист Дж. Карданов 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений

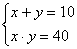не имеющая решений во множестве действительных чисел, имеет решения вида 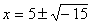, , 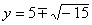нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что .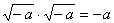

Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название "мнимые числа" ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа 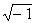(мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу. Термин "комплексные числа" так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.

В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование.

В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический анализ уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие уравнения встречаются, например, в теории колебаний материальной точки в сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял комплексные числа для решения интегралов.

Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения.

Стало ясно, что комплексные числа полезны во многих вопросах, где имеют дело с величинами, которые изображаются векторами на плоскости: при изучении течения жидкости, задач теории упругости.

Комплексные числа (мнимые числа) не являются числами в элементарном смысле слова, применяемыми при подсчетах и измерениях. Они составляют новый класс математических объектов, определяемый свойствами.

Комплексным числом Z называется выражение вида: a + bi, где a и b - действительные числа, а символ i² = -1. Число a - действительная часть, bi - мнимая часть, i - мнимая единица.

C - множество комплексных чисел. Множество действительных чисел входит во множество C. Всякое действительное число можно рассматривать: Z = a + 0i. Комплексное число Z = bi - чисто мнимое. Оно получается из комплексных чисел при a = 0.