Эта игра пришла к нам из Китая. Для нее не нужно доски, фигур или других приспособ­лений. Достаточно набрать немного камешков и разложить их в две кучки. Теперь двое иг­рающих по очереди берут камешки из этих кучек. Разрешается взять за один ход любое количество камешков из одной кучки или из двух кучек, но поровну. Выигрывает тот, кто своим ходом забирает все оставшиеся камни.

Несмотря на простоту условий этой игры, указать, кто выигрывает при конкретном набо­ре камешков, и найти выигрывающую страте­гию в этой игре довольно сложно. Но попытаем­ся это сделать. Если в одной из кучек вообще нет камней, то, очевидно, выигрывает начи­нающий — он забирает всю вторую кучу кам­ней. То же самое происходит, если в кучах одинаковое количество камней.

Результаты анализа ситуаций в игре мы бу­дем заносить в таблицу. Набору камешков, ска­жем, 6 в первой кучке и 8 во второй в таблице соответствует клетка, стоящая на пересечении строки с цифрой 6 и столбца с цифрой 8. Если при некотором наборе камешков выигрывает тот, кто должен ходить, то мы ставим в этой клетке плюс, а если его партнер, то — минус.

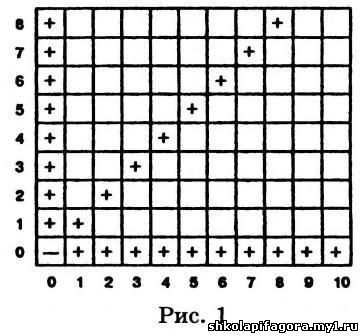
Каждую клетку будем обозначать соответ­ствующей парой чисел. Например, упомяну­тую клетку будем обозначать (8, 6). В клетке (О, 0), очевидно, следует поставить минус, а в клетках (к, 0), (0, к) и (к, к) для всех А, боль­ших нуля, следует поставить плюс. Таблица начала заполняться (рис. 1).

Рассмотрим клетки (1, 2) и (2, 1). Любой ход из этих наборов ведет в клетку, уже поме­ченную знаком плюс, поэтому в этих клетках следует поставить минус, а знаком плюс нужно пометить все клетки, из которых за один ход можно попасть в клетку (1, 2) или (2, 1) (рис. 2).

Теперь выясняется, что любой ход из кле­ток (3, 5) и (5, 3) ведет в клетку, уже помечен­ную знаком плюс, а это значит, что и эти две клетки следует пометить знаками минус, а те клетки, из которых за один ход можно попасть в них, следует пометить знаком плюс (рис. 3).

Глядя на полученный рисунок, отмечаем, что знаком минус следует пометить клетки (4, 7) и (7, 4). Продолжая этот процесс, полу­чаем, что минусом следует пометить клетки (6, 10) и (10, 6). Дальше получаем минусовые клетки (8, 13) и (13, 8), потом (9, 15) и (15, 9), (11, 18) и (18, 11). Можно продолжать этот процесс дальше и дальше, но попробуем по­нять, какому закону подчиняются эти пары чисел.

Будем рассматривать только те пары чи­сел, у которых первое число меньше второго,

потому что остальные получаются изменени­ем порядка чисел в паре. Нетрудно заметить, что разность между вторым и первым числом в паре на каждом шаге увеличивалась на еди­ницу. Кроме того, первое число пары всегда является наименьшим целым числом, не по­павшим еще ни в одну из пар.

Этих данных достаточно, чтобы теперь мож­но было выписывать пары, не заполняя табли­цы. Конечно же, высказанные утверждения нужно строго доказать, что математиками уже было сделано, но попробуйте это сделать и сами.

Итак, получаем последовательность пар чисел: (0, 0), (1, 2), (3, 5), (4, 7), (6, 10), (8, 13), (9, 15), (11, 18), (12, 20), (14, 23), (16, 26), ... Закономерность никак не просматривается, и никаких идей не приходит в голову. Оказыва­ется, что распределение чисел в парах связа­но с числами Фибоначчи, о которых в этой книге помещен специальный рассказ. Это числа 1, 1, 2, 3, 5, 8, 13,..., каждое из кото­рых равно сумме двух предыдущих.

Мы знаем о десятичной и двоичной систе­мах счисления и можем представить систему счисления с любым другим основанием, а те­перь давайте познакомимся с фибоначчиевой системой счисления. Всякое натуральное чис­ло п можно представить в виде суммы чисел Фибоначчи. Сначала возьмем наибольшее число Фибоначчи, не превосходящее п, и вы­чтем его из п. Потом возьмем наибольшее чис­ло Фибоначчи, не превосходящее этой разно­сти, и вычтем его из этой разности, повторим такую процедуру с новой разностью и т. д. На­пример, 17 = 13 + 3 + 1.

Теперь запишем представление числа в си­стеме счисления Фибоначчи. Для числа 17 это будет выглядеть следующим образом. Смотрим, есть ли среди слагаемых число 1? Да. Ставим последней на последнем месте ци­фру 1. Смотрим, есть ли среди слагаемых чис­ло 2? Нет. В этом случае ставим второй циф­рой 0. Дальше проверяем наличие в сумме чи­сел 3, 5, 8, 13 и ставим на очередное место ли­бо 0, либо 1, в зависимости от того, есть такое число в сумме или нет. Для числа 17 получа­ем запись 100101. Обратим внимание на то, что в фибоначчиевой записи числа не может быть двух единиц подряд.

Теперь запишем найденные пары чисел в фибоначчиевой системе счисления. Получим (1, 10), (100, 1000), (101, 1010), (1001, 10010), (10000, 100000), (10001, 100010)... Теперь за­кон уже виден: числа, стоящие первыми, име­ют в фибоначчиевой системе счисления на конце четное число нулей (в частности, нуль нулей), а второе число получается из первого приписыванием одного нуля.