Соотношения между логическими
переменными и логическими функциями в алгебре логики можно отобразить
также с помощью соответствующих таблиц, которые носят название таблиц
истинности. Таблицы истинности находят широкое применение, поскольку
наглядно показывают, какие значения принимает логическая функция при
всех сочетаниях значений ее логических переменных. Таблица истинности
состоит из двух частей. Первая (левая) часть относится к логическим
переменным и содержит полный перечень возможных комбинаций логических
переменных А, В, С… и т. д. Вторая (правая) часть этой таблицы определяет выходные состояния как логическую функцию от комбинаций входных величин.
Например, для логической функции F = A v B v C (дизъюнкции) трех логических переменных А, В, и С таблица
истинности будет иметь вид, показанный на рис. 4.1. Для записи значений
логических переменных и логической функции данная таблица истинности
содержит 8 строк и 4 столбца, т. е. число строк для записи значений
аргументов и функции любой таблицы истинности будет равно 2n, где п – число аргументов логической функции, а число столбцов равно п + 1. Рис. 4.1. Таблица истинности для логической функции F = A v В v С
Таблицу
истинности можно составить для любой логической функции, например, на
рис. 4.2 приведена таблица истинности логической функции F = A ⇔ B ⇔ C (эквиваленции).
Логические функции имеют соответствующие
названия. Для двух двоичных переменных существует шестнадцать логических
функций, названия которых приведены ниже. На рис. 4.3 представлена
таблица, в которой приведены логические функции F1, F2, F3, … , F16 двух логических переменных A и В.
Функция F1 = 0 и называется функцией константы нуля, или генератора нуля. Рис. 4.2. Таблица истинности для логической функции F = A ⇔ B ⇔ C Рис. 4.3. Логические функции F1, F2, F3,… F16 двух аргументов А и В
Функция F2 = A & B называется функцией конъюнкции.
Функция называется функцией запрета по логической переменной А.
Функция F4 = А называется функцией повторения по логической переменной А.
Функция называется функцией запрета по логической переменной В.
Функция F6 = В называется функцией повторения по логической переменной В.
Функция называется функцией исключающее «ИЛИ».
Функция F8 = A v В называется функцией дизъюнкции.
Функция называется функцией Пирса.
Функция называется функцией эквиваленции.
Функция называется функцией отрицания (инверсии) по логической переменной В.
Функция F12 = B ⇒ A называется функцией импликации B ⇒ A.
Функция называется функцией отрицания (инверсии) по логической переменной А.
Функция F14 = A ⇒ B называется функцией импликации A ⇒ B.
Функция называется функцией Шеффера.
Функция F16 = 1 называется функцией генератора 1.
Среди
перечисленных выше логических функций переменных можно выделить
несколько логических функций, с помощью которых можно выразить другие
логические функции. Операцию замены одной логической функции другой в
алгебре логики называют операцией суперпозиции или методом суперпозиции.
Например, функцию Шеффера можно выразить при помощи логических функций
дизъюнкции и отрицания, используя закон де Моргана:
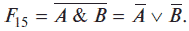 Логические
функции, с помощью которых можно выразить другие логические функции
методом суперпозиции, называются базовыми логическими функциями. Такой
набор базовых логических функций называется функционально полным набором
логических функций. На практике наиболее широко в качестве такого
набора используют три логических функции: конъюнкцию, дизъюнкцию и
отрицание. Если логическая функция представлена с помощью базовых
функций, то такая форма представления называется нормальной. В
предыдущем примере логическая функция Шеффера, выраженная через базовые
функции, представлена в нормальной форме.
При помощи набора базовых функций и
соответствующих им технических устройств, реализующих эти логические
функции, можно разработать и создать любое логическое устройство или
систему.
В настоящее время существует достаточно
много программных продуктов, с помощью которых можно реализовать
различные логические функции и форму их представления, например в виде
таблиц истинности. Логические функции широко используются и в программе MS Excel. Для вызова этих функций необходимо выполнить следующие команды: [Кнопка Пуск – Программы – MS Office ХР – Microsoft Excel] и
далее команду: [Вставка – Функция]. В открывшемся окне (рис. 4.4)
«Мастер функций – шаг 1 из 2», выберем: «Категория: „Логические" и далее
можно выбрать необходимую логическую функцию: ЕСЛИ, И, ИЛИ, ИСТИНА,
ЛОЖЬ, НЕ. В этом же окне можно получить справку по каждой из этих
функций. Рис. 4.4. Диалоговое окно «Мастер функций – шаг 1 из 2»
Как видно из рис. 4.4, в состав логических функций программы MS Excel входит
функционально полный набор логических функций, состоящий из следующих
логических функций: И (конъюнкция), ИЛИ (дизъюнкция), НЕ (отрицание).
Таким образом, с помощью функционально полного набора логических функций
программы MS Excel можно реализовать другие функции. Логическая функция ЕСЛИ (импликация), также входящая в логические функции MS Excel, выполняет
логическую проверку и в зависимости от результата проверки выполняет
одно из двух возможных действий. В данной программе она имеет следующий
формат: = ЕСЛИ (арг1;арг2;арг3), где арг1 – логическое условие; арг2 –
возвращаемое значение при условии, что значение аргумента арг1
выполняется (ИСТИНА); арг3 – возвращаемое значение при условии, что
значение аргумента арг1 не выполняется (ЛОЖЬ). Например, если в
произвольную ячейку листа программы MS Excel ввести выражение « =
ЕСЛИ (А1 = 5; „пять"; „не пять")», то при вводе числа 5 в ячейку А1 и
нажатии клавиши «Enter» в ячейке А1 автоматически будет записано слово
«пять», при вводе любого другого числа в ячейку А1 в ней запишется слово
«не пять». Как уже отмечалось, с помощью логических функций программы MS Excel можно представить другие логические функции и соответствующие им таблицы истинности.
Реализуем с помощью логических функций ЕСЛИ и И модифицированную таблицу истинности логической функции F = А & В (конъюнкции), состоящую из двух строк и трех столбцов, которая позволяет при изменении значений (0 или 1) логических переменных А и В автоматически устанавливать, например, в ячейке Е6 значение функции F = А & В, соответствующее
значениям этих логических переменных. Для этого в ячейку Е6 введем
следующее выражение: «=ЕСЛИ(И(С6;D6);1;0)», тогда при вводе в ячейки С6 и
D6 значений 0 или 1 в ячейке Е6 будет выполняться логическая функция F = А & В. Результат этих действий представлен на рис. 4.5. Рис. 4.5. Реализация модифицированной таблицы истинности логической функции F = A & В
| 
