На экзамене по геометрии очень важно давать правильные (корректные) определения. Часто допускаются такие ошибки, как «порочный круг» (например, круг – это часть плоскости, ограниченной окружностью, а окружность – это граница круга), наличие синонима определяемого термина в определении, пропуск «несущественных деталей» (например, касательная к окружности – это прямая, имеющая с окружностью одну общую точку, «деталь» – это тот факт, что прямая должна лежать с окружностью в одной плоскости).

Определения геометрических фигур можно дать различными способами:

1. Через род и видовое отличие.

Например: квадрат – это прямоугольник с равными сторонами. Прямоугольник в определении – ближайший род, равенство сторон – видовое отличие.

2. Генетически (указание происхождения понятия).

Например, окружность – это множество точек плоскости, находящихся на равном расстоянии от данной точки, лежащей в этой плоскости.

3. Через указание свойств фигуры (дескрипции).

Пример: число ? – это то число, которое, будучи умножено на длину диаметра, даёт длину его окружности.

4. Конструктивно (указывается способ построения объекта).

Пример: пусть дана произвольная окружность. Разделим её на n равных частей последовательно расположенными точками А1, А2..., Ап. Замкнутая ломаная A1A2...АnА1 образует правильный n-угольник.

5. Аксиоматически.

К примеру, определение площади фигуры F даётся как числовая функция S(F), удовлетворяющая определённым условиям (аксиомам).

Другие способы дачи определений в геометрии встречаются крайне редко.

Перейдём к определениям.

Неопределяемыми геометрическими фигурами на плоскости являются точка и прямая.

Точки принято обозначать прописными латинскими буквами: А, В, С, D .... Прямые обозначаются строчными латинскими буквами: а, b, с, d ....

Точка А лежит на прямой а, точка В лежит на прямой b, точка О принадлежит одновременно прямым а и b, т. е. является точкой пересечения этих прямых (рис. 1).

Рис. 1.

Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти две точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок АВ», то подразумевают отрезок с концами в точках А и В (рис. 2).

Рис. 2.

[АВ] – отрезок АВ.

Прямая разбивает плоскость на две полуплоскости. Это разбиение обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.

Отрезок АВ не пересекает прямую а, отрезок АС пересекает прямую а (рис. 3).

Рис. 3.

Лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой луча. Различные лучи одной и той же прямой, имеющие общую начальную точку, называют дополнительными (рис. 4).

Рис. 4.

Лучи, так же как и прямые, обозначаются строчными латинскими буквами. Точка А является начальной точкой двух лучей p и q. Лучи p и q являются дополнительными.

Углом называется фигура, которая состоит из точки – вершины угла – и двух различных лучей или отрезков, исходящих из этой точки – сторон угла. Слово «угол» иногда заменяют знаком ? (рис. 5, 6).

Рис. 5.

Рис. 6.

На рис. 5 угол ? = ?АОВ образован двумя отрезками ОА и ОВ.

На рис. 6 угол ? образован двумя лучами р и q, имеющими начальную точку О.

Если стороны угла являются дополнительными лучами одной прямой, то угол называют развёрнутым (рис. 7).

Рис. 7.

Угол А является здесь развёрнутым.

Луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок, соединяющий любые две точки, лежащие на разных сторонах угла.

Луч q проходит между сторонами ОА и OB угла AOB (рис. 8).

Рис. 8.

Углы измеряют в градусах и радианах. При этом ? радиан = 180°.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами (рис. 9).

Рис. 9.

Сумма смежных углов равна 180°.

Лучи p и q – дополнительные, точка В принадлежит лучу p а точка А принадлежит лучу q. Углы СОА и СОВ – смежные.

Угол, равный 90°, называется прямым.

Угол, меньший 90°, называют острым углом. Угол, больший 90° и меньший 180°, называют тупым (рис. 10, а; б; в).

Рис. 10.

Углы:?АОВ – прямой, ?COD – острый, ?EOF – тупой.

На рисунках прямые углы часто обозначают знаками ?, ?.

Два угла называют вертикальными, если стороны одного угла являются дополнительными лучами сторон другого (рис. 11).

Рис. 11.

р и q – дополнительные лучи одной прямой, а m и n – дополнительные лучи другой прямой. Точка О – точка пересечения этих двух прямых и является начальной точкой всех указанных выше лучей.

Точки А, В, С, D лежат на соответствующих лучах.

Углы АОВ и COD – вертикальные.

Две прямые называют перпендикулярными, если они пересекаются под прямым углом. Перпендикулярность прямых обозначается знаком ? (рис. 12):

а ? b.

Рис. 12.

Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.

Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра (рис. 13):

АA' – перпендикуляр к прямой a, A' – обоснование перпендикуляра.

Рис. 13.

Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам (рис. 14).

Рис. 14.

ОС – биссектриса угла АОВ (?АОС = ?ВОС).

Пусть две прямые a и b пересечены прямой с.

Прямая с по отношению к прямым a и b называется секущей (рис. 15).

Рис. 15.

Углы 3 и 5 (4 и 6) называются внутренними накрест лежащими, углы 3 и 6 (4 и 5) – внутренними односторонними, углы 1 и 6 (2 и 5) – соответственными.

Две прямые называются параллельными, если они не пересекаются. Для обозначения параллельности прямых используется знак||(рис. 16):

а||b.

Рис. 16.

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами (рис. 17):

?ABC.

Рис. 17.

Углом треугольника ABC при вершине А называется угол, образованный отрезками АВ и АС. Также определяются углы треугольника при вершинах В и С.

Две фигуры называются равными, если они при наложении друг на друга совпадают (т. е. существует движение, переводящее одну фигуру в другую). Таким образом, треугольники равны, если у них соответствующие стороны и соответствующие углы равны (при этом соответствующие углы лежат против соответствующих сторон).

Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника (рис. 18).

Рис. 18.

?ABC – равнобедренный (АВ = ВС – боковые стороны, АС – основание).

Треугольник, у которого все стороны равны, называется равносторонним (рис. 19).

Рис. 19.

? DEF– равносторонний (DE = EF = DF).

Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведённый из этой вершины к прямой, которая содержит противолежащую сторону треугольника (рис. 20, а; б).

Рис. 20.

ВН – высота в треугольнике ABC (ВН ? АС).

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне (рис. 21).

Рис. 21.

AL – биссектриса в треугольнике ABC (?BAL = ?CAL).

Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны треугольника (рис. 22).

Рис. 22.

AM – медиана треугольника ABC (BM = MC).

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине (рис. 23).

Рис. 23.

? – внешний угол ?ABC при вершине А.

Треугольник называется прямоугольным, если у него есть прямой угол (рис. 24).

Рис. 24.

Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.

?ABC – прямоугольный (?А = 90°). АВ и АС – катеты, ВС – гипотенуза.

Треугольник называется остроугольным, если все его углы – острые. Треугольник называется тупоугольным, если у него есть тупой угол.

?ABC – остроугольный, ?А < 90° (рис. 25, а);

?ABC – тупоугольный, ?А > 90° (рис. 25, б).

Рис. 25.

Средней линией треугольника называется отрезок, соединяющий середины двух любых сторон треугольника (рис. 26).

Рис. 26.

EF – средняя линия ?ABC (АЕ = ЕВ. CF = FB).

Египетским называется прямоугольный треугольник, у которого длины сторон выражаются целыми числами (например:3, 4, 5 или 5, 12, 13 и так далее).

Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от заданной точки. Эта заданная точка называется центром окружности.

Расстояние от точек окружности до её центра называется радиусом окружности. Радиусом называется также отрезок, соединяющий любую точку окружности с её центром (рис. 27).

Рис. 27.

ОА – радиус окружности.

Радиусы окружностей часто обозначают буквами R или r, т. е. ОА = R или ОА = r.

Круг – это часть плоскости, ограниченная окружностью (рис. 28).

Рис. 28.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром окружности (рис. 29).

Рис. 29.

АВ – диаметр окружности, CD – хорда.

Диаметры окружностей часто обозначают буквами D или d. Очевидно, что D = 2R или d = 2 r.

Дуга окружности – это её часть, ограниченная двумя точками окружности (рис. 30).

Рис. 30.

Точки А и В делят окружность на две дуги:1 и 2.

Сектор круга – часть круга, ограниченная двумя радиусами и соответствующей дугой (рис. 31).

Рис. 31.

Радиусы ОА и ОВ разделили круг на два сектора:1 и 2.

Сегмент круга – это часть круга, ограниченная хордой и соответствующей дугой (рис. 32).

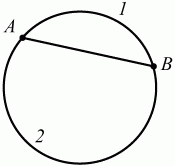Рис. 32.

Хорда АВ делит круг на два сегмента:1 и 2.

Окружность называется описанной около треугольника, если она проходит через все его вершины (рис. 33).

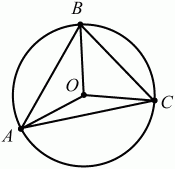Рис. 33.

ОА = ОВ = ОС = R.

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром (рис. 34). В связи с этим говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.

а – серединный перпендикуляр к отрезку АВ (АО = ОВ).

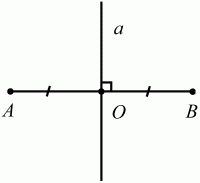Рис. 34.

Прямая, проходящая через точку окружности в той же плоскости перпендикулярно к радиусу, проведённому в эту точку, называется касательной. При этом данная точка окружности называется точкой касания (рис. 35).

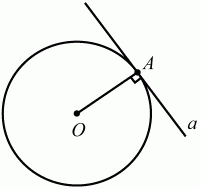Рис. 35.

а – касательная к окружности, А – точка касания, а ? ОА.

Говорят, что две окружности, имеющие общую точку, касаются в этой точке, если они имеют в этой точке общую касательную. Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной. Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной (рис. 36, а; б).

Рис. 36.

а – общая касательная к двум окружностям, К – точка касания.

Окружность называется вписанной в треугольник, если она касается всех его сторон (рис. 37).

Рис. 37.

Точки K, L, M – это точки касания окружности, вписанной в ?ABC. OK = OL = OM = r.

В задачах на построение речь идет о построении геометрической фигуры с помощью данных чертёжных инструментов. Такими инструментами чаще всего являются линейка и циркуль. Решение задачи состоит не столько в построении фигуры, сколько в решении вопроса о том, как это сделать, и соответствующем доказательстве. Задача считается решённой, если указан способ построения фигуры и доказано, что в результате выполнения указанных построений действительно получается фигура с требуемыми свойствами.

С помощью линейки, как инструмента геометрических построений, можно провести произвольную прямую; произвольную прямую, проходящую через данную точку; прямую, проходящую через две данные точки. Никаких других операций выполнить линейкой нельзя. В частности, нельзя откладывать линейкой отрезки, даже если на ней имеются деления.

Циркуль, как инструмент геометрических построений, позволяет описать из данного центра окружность определенного радиуса. Циркулем также можно отложить определенный отрезок на данной прямой от заданной точки.

Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определённым свойством.

Например, окружность можно определить как геометрическое место точек плоскости, равноудалённых от данной точки.

Сущность метода геометрических мест, используемого при решении задач, состоит в следующем. Пусть, решая задачу, нам надо найти точку X, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть некоторая фигура F1, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F2. Искомая точка X принадлежит F1 и F2 т. е. является их точкой пересечения. Если эти геометрические места простые (скажем, состоят из прямых и окружностей), то мы можем их построить и найти интересующую нас точку X.

Ломаной А1А2А3...An называется фигура, которая состоит из точек А1, А2 ..., An и соединяющих их отрезков А1A2, A2A3, ..., An-1, Aп. ТочкиА1, А2..., Аn называются вершинами ломаной, а отрезки A142, A2A3 ..., An-1, An – звеньями ломаной. Ломаная называется простой, если она не имеет самопересечений (рис. 38).

Рис. 38.

А1A2A3A4 – простая ломаная из трёх звеньев.

Ломаная называется замкнутой, если у неё концы совпадают. Простая замкнутая ломаная называется многоугольником, если её соседние звенья не лежат на одной прямой. Вершины ломаной называются вершинами многоугольника, а звенья ломаной – сторонами многоугольника. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями. Многоугольник с n-вершинами, а значит, и с n-сторонами называется n-угольником.

Плоским многоугольником и многоугольной областью называется конечная часть плоскости, ограниченная многоугольником.

Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону (рис. 39). Многоугольник называется невыпуклым, если он оказывается лежащим по обе стороны прямой, содержащей любую его сторону (рис. 40).

Рис. 39.

Рис. 40.

Выпуклый многоугольник называют правильным, если у него все стороны равны и все углы равны.

Многоугольник называется вписанным в окружность, если все его вершины лежат на некоторой окружности. Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.

Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины многоугольника, называются диагоналями.

Стороны многоугольника, исходящие из одной вершины, называются соседними сторонами. Стороны, не имеющие общего конца, называются противолежащими сторонами.

Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны, т. е. лежат на параллельных прямых (рис. 41).

Рис. 41.

ABCD – параллелограмм, т. к. ВС||AD и АВ||CD.

Прямоугольник – это параллелограмм, у которого все углы прямые (рис. 42).

Рис. 42.

ABCD – прямоугольник, т. к. ?А = ?В = ?С = ?D = 90°.

Ромб – это параллелограмм, у которого все стороны равны (рис. 43).

Рис. 43.

ABCD – ромб, т. к. AD||ВС и АВ||DC и AB = BC = CD = AD.

Квадрат – это прямоугольник, у которого все стороны равны. Можно также сказать, что квадрат – это ромб, у которого все углы прямые (рис. 44).

Рис. 44.

ABCD – квадрат, т. к. ?А = ?В = ?С = ?D = 90° и АВ = ВС = CD = DA.

Трапецией называется четырёхугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами (рис. 45).

Рис. 45.

ABCD и А' В' С' D' – трапеции, т. к. BC||AD, BC||AD.

Трапеция, у которой боковые стороны равны, называется раенобокой (рис. 46).

Рис. 46.

ABCD – равнобедренная трапеция (АВ = CD).

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции (рис. 47).

Рис. 47.

EF – средняя линия трапеции ABCD: AE = EB, DF = FC.

Пусть ВА – перпендикуляр, опущенный из точки В на прямую а, и С – любая точка прямой а, отличная от А. Отрезок ВС называется наклонной, проведённой из точки В к прямой а. Точка С называется основанием наклонной. Отрезок АС называется проекцией наклонной (рис. 48).

Рис. 48.

ВА – перпендикуляр к прямой а, ВС – наклонная.

Проведём на плоскости через точку О две взаимно перпендикулярные прямые х и у – оси координат. Ось х (она обычно горизонтальная) называется осью абсцисс, а ось у – осью ординат. Точкой пересечения О – началом координат – каждая из осей разбивается на две полуоси. Условимся одну из полуосей каждой оси называть положительной, отмечая её стрелкой, а другую – отрицательной.

Каждой точке А плоскости мы сопоставим пару чисел – координаты точки – абсциссу х и ординату у по следующему правилу.

Через точку А проведём прямую, параллельную оси ординат. Она пересечёт ось абсцисс х в некоторой точке Аx. Абсциссой точки А мы будем называть число х, абсолютная величина которого равна расстоянию от точки О до точки Аx. Это число будет положительным, если Аx принадлежит положительной полуоси и отрицательным, если А принадлежит отрицательной полуоси. Если точка А лежит на оси ординат y, то полагаем х равным нулю.

Ордината j точки А определяется аналогично. Через точку А проведём прямую, параллельную оси абсцисс х. Она пересечёт ось ординату в некоторой точке Аy. Ординатой точки А мы будем называть число у, абсолютная величина которого равна расстоянию от точки О до точки Аy. Это число будет положительным, если Аy принадлежит положительной полуоси, и отрицательным, если А принадлежит отрицательной полуоси. Если точка А лежит на оси абсцисс х, то полагаем у равным нулю.

Координаты точки записывают в скобках рядом с буквенным обозначением точки, например: А(х; у) (на первом месте абсцисса, на втором – ордината) (рис. 49).

Рис. 49.

Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя неизвестными х и у, которому удовлетворяют координаты любой точки фигуры.

Например, уравнение прямой у = kx + b, где k – тангенс угла наклона прямой к оси Ох (рис. 50).

Рис. 50.

Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной. Симметрия относительно точки, симметрия относительно прямой, поворот, параллельный перенос – виды движений.

Два отрезка называют одинаково направленными, или сонаправленными, если они совмещаются параллельным переносом.

Векторы АВ и CD называют одинаково направленными, если отрезки АВ и CD одинаково направлены. Векторы АВ и CD называют противоположно направленными, если отрезки АВ и CD противоположно направлены. Первая буква в обозначении вектора является его началом, а вторая буква – его концом. Например, у вектора АВ точка А – начало вектора, а точка В – его конец (рис. 51).

Рис. 51.

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Обозначают модуль вектора (на пример, АВ) следующим образом:|АВ|. Очевидно, что |AB| = AB, где АВ – это длина отрезка АВ.

Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором.

Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора (рис. 52).

Рис. 52.

Пусть вектор а имеет началом точку А1(х1; у1), а концом точку А2(х2; у2). Координатами вектора а будем называть числа a1 = x2 – x1, a2 = y2 – y1.

Суммой векторов а и b с координатами а1, а2 и BL, b2 называется вектор с с координатами a1 + BL, a2 + b2.

Разностью векторов а (a1; a2) и b (BL; b2) называется такой вектор с (с1; с2), который в сумме с вектором b даёт вектор а, т. е. b + с = а. Отсюда находим координаты вектора с = а – b: с1 = а1 – BL: с2 = а2 – b2.

Удобно производить разложение вектора по двум перпендикулярным осям. В этом случае составляющие вектора называются проекциями вектора на оси.

Произведением вектора а (a1; a2) на число k называется вектор с координатами (kа1; kа2).

Два вектора а и b называются коллинеарными (параллельными), если существует такое число k ? 0, что вектор а есть kb.

Разложить вектор а по векторам b и с – значит найти такие числа n, m, что а = nb + mc.

Скалярным произведением векторов а (a1; a2) и b (BL; b2) называют число a1BL + a2b2.

Углом между ненулевыми векторами АВ и АС называется угол ВАС. Углом между любыми двумя ненулевыми векторами а и b называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю.

Если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.

Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления положительных координатных полуосей, называют координатными векторами или ортами.

Преобразование фигуры F в фигуру F1 называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз. Это значит, что если произвольные точки X, Y фигуры F при преобразовании подобия переходят в точки X1, Y1 фигуры F1, то X1Y1 = k ? ХУ, причём число k – одно и то же для всех точек X, Y. Число k называется коэффициентом подобия. При k = 1 преобразование подобия, очевидно, является движением.

Пусть F – данная фигура и О – фиксированная точка. Проведём через произвольную точку X фигуры F отрезок ОХ и отложим на нём отрезок ОХ1 равный k ? ОХ, где k – положительное число. Преобразование фигуры F, при котором каждая её точка X переходит в точку X1 построенную указанным способом, называется гомотетией относительно центра О. Число k называется коэффициентом гомотетии, фигуры F и F1 называют гомотетичными.

На рис. 53 ?АВС и ?A1В1С1 – гомотетичны.

Рис. 53.

Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия.

Угол разбивает плоскость на две части. Каждая из частей называется плоским углом. Плоские углы с общими сторонами называются дополнительными.

Центральным углом в окружности называется плоский угол с вершиной в её центре. Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу. Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла (рис. 54).

?АОВ (угол ?) – центральный.

Рис. 54.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность (рис. 55).

Рис. 55.

?АСВ (угол ?) – вписанный.

Геометрическую фигуру будем называть простой, если её можно разбить на конечное число плоских треугольников. Напомним, что плоским треугольником мы называем конечную часть плоскости, ограниченную треугольником.

Дадим определение площади для простых фигур.

Для простых фигур площадь – это положительная величина, численное значение которой обладает следующими свойствами:

1. Равные фигуры имеют равные площади.

2. Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей.

3. Площадь квадрата со стороной, равной единице, равна единице.