При решении вычислительных задач на треугольник нужно знать следующие формулы (рис. 125):
Рис. 125.
где a, b, с – стороны треугольника;
?, ?, ? – противолежащие им углы;
r и R – радиусы вписанной и описанной окружностей;
ha, ma, la – высота, медиана и биссектриса, проведённые к стороне а;
S – площадь треугольника;
– полупериметр треугольника.
Иногда применяют формулу
а также формулу расстояния между центрами описанной и вписанной окружностей:
Примеры решения задач
1. Определите вид треугольника (остроугольный, тупоугольный или прямоугольный) со сторонами 8, 6 и 11 см (рис. 126).
Рис. 126.
Решение.
Обозначим больший угол треугольника через ?. Очевидно, что он лежит
напротив стороны в 11 см, так как в треугольнике больший угол лежит
против большей стороны. По теореме косинусов 112= 82+ 62– 2?8?6?cos ?;
cos ? = -7/32 < 0, значит, угол ? – тупой.
Можно было рассуждать и по-другому. Если бы угол ? был равен 90°, то большая сторона по теореме Пифагора равнялась бы
Удлинение стороны на 1 см автоматически увеличивает и лежащий напротив угол – он становится тупым.
Ответ: тупоугольный.
2. Основание
треугольника равно 6 см, один из углов при основании равен 105°, другой
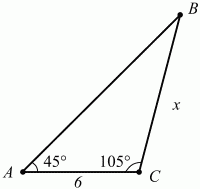
– 45°. Найдите длину стороны, лежащей против угла в 45° (рис. 127).
Рис. 127.
Решение.
Пусть в треугольнике ABC будут АС = 6 см, ?А = 45°, ?С = 105°.
Обозначим длину стороны ВС через х. Её нам и нужно найти. Воспользуемся
теоремой синусов по которой:
Учитывая, что сумма углов в треугольнике равна 180°, получим:?В = 180° – ?A – ?C = 180°– 45°– 105° = 30°.
Итого
Ответ:
3. Найдите площадь треугольника со сторонами 2, ?5 и 3 (рис. 128).
Рис. 128.
Решение. Можно воспользоваться формулой Герона:
В нашем случае:
Полупериметр:
Проще решить задачу можно было бы так. По теореме косинусов:
Так как площадь треугольника равна половине произведения двух сторон на синус угла между ними, то:
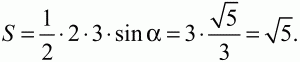 Ответ: ?5.
4. В треугольнике ABC, где ?ACB = 120°, проведена медиана СМ. Найдите ее длину, если АС = 6, ВС = 4 (рис. 129).
Рис. 129.
Решение. Воспользуемся формулой длины медианы
У
нас а = ВС = 4, b = АС = 6. Осталось найти с = АВ. Применим к
треугольнику АСВ теорему косинусов: с2= АВ2= АС2+ ВС2– 2AC ? BC
? cos(?АСВ) = 62+ 42– 2 ? 6 ? 4 ? cos 120° = 36 + 16–48?(-1/2) = 76.
Ответ: ?7.
5. Найдите
длины сторон АВ и АС остроугольного треугольника ABC, если ВС = 8, а
длины высот, опущенных на стороны АС и ВС, равны 6, 4 и 4 соответственно
(рис. 130).
Рис. 130.
Решение. Единственный угол треугольника, который остался «нетронутым», угол С.
Из прямоугольного треугольника ВМС следует:
тогда
Из ?АКС:
А теперь по теореме косинусов, применённой к треугольнику ABC, получаем:
Ответ: AB = ?41; AC = 5.
6. В
треугольнике, один из углов которого равен разности двух других, длина
меньшей стороны равна 1, а сумма площадей квадратов, построенных на двух
других сторонах, в два раза больше площади описанного около
треугольника круга. Найти длину большей стороны треугольника (рис. 131).
Рис. 131.
Решение:
Обозначим через ? наименьший угол в треугольнике и через ? наибольший
угол. Тогда третий угол равен ? – ? – ?. По условию задачи ? – ? = ? – ?
– ? (больший угол не может равняться разности двух других углов).
Отсюда следует, что 2? = ?; ? = ?/2. Значит, треугольник прямоугольный.
Катет ВС, лежащий против меньшего угла ?, равен по условию 1, значит,
второй катет АВ равен ctg?, а гипотенуза АС равна 1/sin ?. Поэтому сумма
площадей квадратов, построенных на гипотенузе и большем катете, равна:
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, и её радиус равен:
а площадь равна:
Пользуясь условием задачи, имеем уравнение:
откуда
Длина большей стороны треугольника равна
Ответ:
7. Длины сторон а, b, с треугольника равны 2, 3 и 4. Найти расстояние между центрами описанной и вписанной окружностей. (2)
Решение. Для решения задачи даже чертеж не нужен. Последовательно находим: полупериметр
Расстояние между центрами окружностей:
Ответ:
8. В
треугольнике ABC величина угла ВАС равна ?/3, длина высоты, опущенной
из вершины С на сторону АВ, равна ?3 см, а радиус окружности, описанной
около треугольника ABC, равен 5 см. Найти длины сторон треугольника ABC
(рис. 132).
Рис. 132.
Решение: Пусть CD – высота треугольника ABC, опущенная из вершины С. Возможны три случая. Основание D высоты CD попадает:
1) на отрезок АВ;
2) на продолжение отрезка АВ за точку В;
3) в точку В.
По условию радиус R окружности, описанной около треугольника ABC, равен 5 см. Следовательно, во всех трех случаях:
Теперь
ясно, что точка D не совпадает с точкой В, так как ВС ? CD. Применяя
теорему Пифагора к треугольникам ACD и BCD, находим, что
Отсюда следует, что точка D лежит между точками А и В, но тогда АВ = AD + BD (1 + 6?2) см.
Ответ: АВ = (6?2 + 1) см, ВС = 5?3 см, АС = 2 см.
9. В
треугольниках ABC и A1B1C1 длина стороны АВ равна длине стороны А1В1,
длина стороны АС равна длине стороны А1С1, величина угла ВАС равна 60° и
величина угла В1А1С1 равна 120°. Известно, что отношение длины В1С1 к
длине ВС равно ?n (где n – целое число). Найти отношение длины АВ к
длине АС. При каких значениях n задача имеет хотя бы одно решение
(рис. 133)?
Рис. 133.
Решение:
Пусть ABC и A1B1C1 – данные в условии задачи треугольники. Применяя
теорему косинусов к треугольникам ABC и А1В1С1, имеем:
Т. к. по условию задачи В1С1 :ВС = ?n, то
Поскольку
А1В1 = АВ и А1С1 = АС, то, разделив числитель и знаменатель дроби в
левой части равенства (1) на АС2и обозначив АВ: АС через х, получим
равенство:
откуда ясно, что искомое отношение длины АВ к длине АС есть корень уравнения
х2(n – 1) – х(n + 1) + n – 1 = 0.
Т. к. В1С1 > ВС, то n > 1.
Следовательно, уравнение является квадратным. Его дискриминант равен
(n + 1)2– 4(n – 1)2= – 3n2+ 10n – 3.
Уравнение (2) будет иметь решения, если –
3n2+ 10n – 3 ? 0, т. е. при -1/3 ? n ? 3. Т. к. n – натуральное число,
большее 1, то уравнение (2) имеет решения при n = 2 и n = 3. При n = 3
уравнение (2) имеет корень х = 1; при n = 2 уравнение имеет корни
Ответ: отношение длины АВ к длине АС равно
при n = 2; равно 1 при n = 3; при остальных n решений нет.
Задачи для самостоятельного решения
10. В треугольнике ABC высота AD на 4 см
меньше стороны ВС. Сторона АС равна 5 см. Найдите периметр треугольника
ABC, если его площадь равна 16 см2.
11. Докажите, что для любого треугольника выполняется равенство:
где ha, hb и hc – высоты треугольника, а r – радиус вписанной окружности.
12. Основание треугольника равно
?2. Найдите длину отрезка прямой, параллельной основанию и делящей
площадь треугольника пополам.
13. Найдите площадь треугольника по стороне а и прилежащим к ней углам ? и ?.
14. В треугольнике ABC длина высоты BD
равна 6 см, длина медианы СЕ равна 5 см, расстояние от точки пересечения
отрезков BD и СЕ до стороны АС равно 1 см. Найти длину стороны АВ.
15. В треугольнике ABC высота BD равна
11,2, а высота АЕ равна 12. Точка Е лежит на стороне ВС, и BE: ЕС = 5:9.
Найти длину стороны АС.
16. В треугольнике ABC длина стороны АС
равна 3, ?ВАС = ?/6 и радиус описанной окружности равен 2. Доказать, что
площадь треугольника ABC меньше 3.
17. В треугольнике ABC медианы,
проведенные к сторонам АС и ВС, пересекаются под прямым углом. Длина
стороны АС равна b, длина стороны ВС равна а. Найти длину стороны АВ.
| 
