Узоры математика, как и узоры художника или узоры поэта, должны быть красивы; идеи, как и краски или слова, должны сочетаться гармонически. Красота является первым критерием: в мире нет места для безобразной математики.

Г. Г. Харди

В январе 1954 года талантливый молодой математик из Токийского университета нанес обычный визит в факультетскую библиотеку. Горо Шимуре был нужен экземпляр журнала «Mathematische Annalen», том 24. В частности, его интересовала статья Дойринга по алгебраической теории комплексного умножения. Шимура надеялся, что теория Дойринга поможет ему выполнить чрезвычайно сложные вычисления, смысл которых был ясен лишь узкому кругу специалистов.

К удивлению и разочарованию Шимуры, нужный ему том журнала был выдан. Его взял Ютака Танияма, с которым Шимура был едва знаком. Танияма жил в другом конце студенческого городка. Шимура отправил Танияме открытку, объясняя, что журнал ему срочно нужен, чтобы закончить сложные вычисления, и вежливо осведомился, когда тот мог бы вернуть журнал.

Через несколько дней на рабочий стол Шимуры легла открытка. Танияма сообщал, что он работает над той же проблемой и столкнулся с той же трудностью, о которой упоминал в своей открытке Шимура. Танияма предложил встретиться для того, чтобы обменяться идеями, и, возможно, в дальнейшем совместно работать над проблемой. Так случайное совпадение заказов на один и тот же журнал в университетской библиотеке стало толчком к сотрудничеству, благодаря которому в математике была найдена одна из фундаментальных закономерностей.

Танияма родился 12 ноября 1927 года в небольшом городке в нескольких километрах к северу от Токио. Японский иероглиф, обозначающий его имя, должен читаться как «Тойо», но большинство чужих людей, не являющихся членами семьи Таниямы, неправильно интерпретировали его как «Ютака», и, когда Танияма вырос, он принял это имя. В детстве образование Таниямы постоянно прерывалось. Он не отличался особенно крепким здоровьем, часто хворал, а став подростком, заболел туберкулезом и пропустил два года в средней школе. Разразившаяся война вызвала еще более продолжительный перерыв в его образовании.

Горо Шимура, бывший на один год младше Таниямы, вынужден был совсем не учиться в военные годы. Его школу закрыли, и вместо уроков Шимура был вынужден работать на заводе, собирая детали самолетов. Каждый вечер он пытался самостоятельно заниматься по школьной программе. Особенно его влекла математика. «Разумеется, приходилось изучать многие предметы, но особенно легко мне давалась математика. Я запоем читал учебники математики. По учебникам я выучил математический анализ. Если бы я захотел изучить химию или физику, то мне потребовалось бы специальное оборудование, а у меня не было доступа ни к чему подобному. Я никогда не думал, будто обладаю какими-то способностями к математике. Просто мне было интересно».

Через несколько лет после окончания войны Шимура и Танияма были уже студентами университета. К тому времени, когда они обменялись открытками по поводу тома «Mathematische Annalen», жизнь в Токио начала возвращаться в обычное русло, и два студента могли позволить себе небольшую роскошь: среди дня немного посидеть в кафе, вечером пообедать в ресторанчике, специализировавшемся на блюдах из китового мяса, а потом погулять в ботаническом саду или городском парке. Все это были идеальные места для обсуждения самых свежих математических идей.

Хотя Шимура был не чужд некоторых причуд (он и поныне питает слабость к анекдотам о мудрецах, проповедующих дзен-буддизм), он был более консервативен и традиционен, чем его коллега. Шимура поднимался на рассвете и сразу же приступал к работе. Танияма же частенько не ложился спать, проработав всю ночь напролет. Те, кто заглядывал днем к нему в номер, нередко заставали его спящим.

Шимура был скрупулезен и строг, Танияма небрежен, почти ленив. Удивительно, но именно эта черта в Танияме особенно импонировала Шимуре: «Он обладал особым даром совершать множество ошибок, в основном в правильном направлении. Я завидовал этой его особенности и даже пытался подражать ему, но обнаружил, что совершать хорошие ошибки очень трудно».

Танияма был живым воплощением рассеянного гения, и это отражалось и на его внешности. Он был неспособен крепко завязать шнурки на ботинках и поэтому решил вместо того, чтобы по десять раз на день делать одно и тоже, вообще их не завязывать. Он всегда носил один и тот же весьма приметный зеленый костюм с металлическим отливом. Костюм был сшит из ткани, настолько кричащей, что остальные члены семьи отказались от нее.

Когда Танияма и Шимура встретились в 1954 году, они оба были начинающими математиками. По традиции, существующей и до сих пор, молодых аспирантов берет «под крыло» профессор, руководящий их становлением как математиков. Танияма и Шимура отвергли такую форму ученичества. Во время войны настоящие математические исследования прекратились, и даже к 50-м годам математический факультет еще не возродился. По словам Шимуры, профессора были «усталы, измучены и разочарованы». Что же касается послевоенных студентов и аспирантов, то они были преисполнены энергии и страстно хотели учиться. Вскоре аспиранты поняли, что единственный доступный им способ изучать математику заключается в том, чтобы обучать друг друга. Они организовали регулярно действующие семинары, на которых по очереди информировали друг друга о новейших идеях, результатах и методах. Несмотря на свою вялость и апатичность, Танияма, когда речь заходила о семинарах, преисполнялся всесокрушающей энергией. Аспирантов постарше он поощрял к тому, чтобы те смелее вторгались на еще неизведанную территорию, а по отношению к аспирантам младше себя и студентам выступал в роли учителя. Научная изоляция Японии привела к тому, что эти семинары занимались задачами, которые, как правило, в Европе и Америке считалась давно пройденными. Одна вышедшая из моды тема, а именно, исследование модулярных форм, казалась особенно привлекательной Танияме и Шимуре, Модулярные формы — один из самых причудливых и чудесных объектов в математике. Современный специалист по теории чисел Эйхлер причислил их к одной из пяти фундаментальных операций, т. е. умение обращаться с модулярными формами он считал настолько же важным, как и выполнение четырех действий арифметики. Надо сказать, что далеко не все математики уверенно чувствуют себя, сталкиваясь с этой пятой операцией, в отличие от первых четырех, где они считают себя мастерами.

Отличительной особенностью модулярных форм является их необычайно высокий уровень симметрии. Хотя большинство людей знакомо с повседневным понятием симметрии, в математике в термин «симметрия» вкладывают особый смысл. Объект считается обладающим симметрией, если его можно преобразовать дозволенным образом так, что преобразованный объект будет неотличим от исходного. Чтобы оценить необычайно высокую симметрию модулярной формы полезно сначала изучить симметрию какого-нибудь более знакомого объекта, например, простого квадрата.

Рис. 18. Простой квадрат обладает вращательной и зеркальной симметриями

Рис. 19. Плоскость, выложенная квадратами, помимо вращательной и зеркальной симметрий обладает еще и трансляционной симметрией

В случае квадрата одна из форм симметрий — вращательная. Если мы мысленно проведем через точку пересечения осей x и y прямую, перпендикулярную рисунку, то квадрат на рис. 18 можно повернуть на четверть оборота — и он будет неотличим от исходного квадрата. Квадрат будет неотличим от исходного и после поворота на пол-оборота, три четверти оборота и полный оборот.

Помимо вращательной симметрии квадрат обладает зеркальной симметрией. Если представить себе, что зеркало расположено вдоль оси x перпендикулярно плоскости рисунка, то верхняя половина квадрата отразится точно на нижнюю и наоборот, поэтому после преобразования квадрат будет неотличим от исходного. Аналогично, мы можем поставить три других зеркала (вдоль оси y и двух диагоналей). Во всех случаях отраженный квадрат будет неотличим от исходного квадрата.

Простой квадрат симметричен, поскольку обладает вращательной и зеркальной симметриями. Но не обладает трансляционной симметрией. Это означает, что если квадрат подвергнуть сдвигу в любом направлении, то наблюдатель тотчас же заметит перемещение, поскольку положение квадрата относительно осей x и y изменится. Но если бы вся плоскость была вымощена квадратами, как на рис. 19, то этот бесконечный набор квадратов обладал бы трансляционной симметрией. При сдвиге такой разбитой на квадраты бесконечной поверхности на расстояние, равное одной или нескольким длинам квадрата, сдвинутая мозаика была бы ничем не отличима от исходной.

Симметрия выложенных плитками поверхностей — идея довольно простая, но, как это нередко бывает со многими простыми на первый взгляд понятиями, в ней скрыто немало тонкостей. Например, в 70-е годы британский физик и большой любитель занимательных задач-головоломок Роджер Пенроуз начал прикидывать различные варианты разбиения одной и той же поверхности на плитки различной формы. В конце концов он обнаружил две особенно интересные формы, которые он назвал воздушным змеем и дротиком (см. рис. 20). Каждая из этих форм сама по себе не годится для замощения всей поверхности без пробелов и наложений плиток друг на друга, но вместе воздушные змеи и дротики позволяют разбивать поверхность на мозаики с различным рисунком. Змеи и дротики можно сочетать бесконечным числом способов, и хотя рисунки мозаик кажутся похожими, они сильно отличаются в деталях. Одна из таких мозаик представлена на рис. 20.

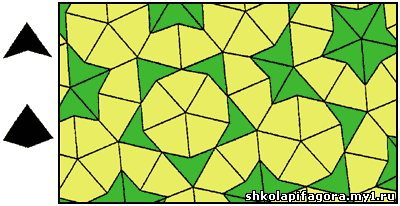
Рис. 20. Используя плитки двух различных форм Роджер Пенроуз сумел выложить ими всю плоскость. Однако мозаика Пенроуза не обладает трансляционной симметрией

Еще одна замечательная особенность мозаик Пенроуза заключается в том, что они обладает весьма ограниченным уровнем симметрии. На первый взгляд может показаться, что мозаика на рис. 20 обладает трансляционной симметрией, тем не менее любая попытка совместить мозаику с самой собой завершается неудачей. Мозаики Пенроуза оказались асимметричными, и этим они так привлекли математиков, что стали исходным пунктом в развитии целого нового направления.

Интересно отметить, что мозаики Пенроуза эхом отозвались в материаловедении. Кристаллографы всегда считали, что структура кристаллов опирается на принципы, лежащие в основе разбиения на квадраты, обладающего высоким уровнем трансляционной симметрии. Теоретически строение кристаллов зиждется на весьма регулярной периодической структуре. Но в 1984 году ученые обнаружили металлический кристалл сплава алюминия и марганца, построенный на тех же принципах, что и мозаики Пенроуза. Мозаика сплава алюминия и марганца вела себя, как мозаика из воздушных змеев и дротиков, порождая кристалл почти регулярный, но не совсем. Недавно одна из французских компаний использовала кристалл Пенроуза в покрытии для сковород.

Если отличительной особенностью мозаик Пенроуза является их ограниченная симметрия, то отличительная особенность модулярных форм — их бесконечная, неисчерпаемая симметрия. Модулярные формы, изучением которых занимались Танияма и Шимура, можно подвергать трансляциям (параллельным переносам, или сдвигам), перестраивать, переставлять фрагменты, отражать в зеркалах и поворачивать бесконечно многими способами, и при этом они останутся неизменными, что делает их наиболее симметричными математическими объектами. Когда французский математик-универсал Анри Пуанкаре изучал модулярные формы в XIX веке, он испытал огромные трудности, пытаясь справиться с их огромной симметрией. Пуанкаре признавался своим коллегам, что получив модулярную форму частного вида, он на протяжении двух недель просыпался каждое утро в надежде найти ошибку в своих вычислениях. И только на пятнадцатый день он понял, что модулярные формы действительно обладают предельно возможной симметрией.

К сожалению, ни нарисовать, ни даже наглядно представить себе модулярную форму невозможно. В случае квадратной мозаики мы имеем объект, который обитает в двух измерениях. Его пространство задано осью x и осью y. Модулярную форму можно представлять себе как функцию, область определения которой находится в двух измерениях, но область значений которой также двумерна. Поэтому если бы мы хотели посмотреть на график такой функции, то он оказался бы в четырехмерном пространстве.

Еще одной особенностью модулярных форм является то, что на области их определения можно ввести специальную структуру, превращающую эту область в гиперболическое пространство. Людям, вынужденным жить в обычном трехмерном мире, понять, что такое гиперболический мир, довольно трудно, но с точки зрения математики именно эта особенность придает модулярным формам столь необычайно высокий уровень симметрии. Голландский художник Мориц Эшер был так увлечен математическими идеями, что попытался воплотить понятие гиперболического пространства в некоторых из своих гравюр и рисунков. На рис. 21 вы видите работу Эшера «Предельный круг. IV», на которой гиперболический мир втиснут в двумерную страницу. В истинно гиперболическом мире все летучие мыши и ангелы были бы одного размера, а повторы указывают на высокий уровень симметрии. Хотя некоторая симметрия ощутима и на рисунке, по мере продвижения к краю картины искажения усиливаются.

Рис. 21. «Предельный круг. IV» Морица Эшера содержит некоторые элементы симметрии модулярных форм

Модулярные формы появляются в различных обличьях, но каждую из форм можно представить в виде бесконечной суммы слагаемых специального вида, которые и отличают одну форму от другой. Эти бесконечные ряды, с помощью которых модулярная форма задается однозначно, называют модулярными рядами, или M-рядами.

Подобно тому, как E-ряды служат своего рода ДНК для эллиптических кривых, M-ряды играют роль ДНК для модулярных форм. Изменяя слагаемые M-ряда можно породить совершенно другую, но столь же симметричную, модулярную форму или полностью разрушить симметрию и создать новый объект, который не является модулярной формой. Если слагаемые выбраны произвольно, то построенный объект скорее всего будет обладать малой симметрией или даже будет полностью асимметричным.

Модулярные формы сами по себе играют весьма важную роль в математике. Они никак не связаны с предметом исследований Уайлса в Кембридже — эллиптическими кривыми. Модулярная форма — объект необычайно сложный, открытый только в XIX веке и ставший предметом пристального изучения главным образом из-за его симметрии. Кубические уравнения, соответствующие эллиптическим кривым, были известны с античных времен и не были никак связаны с симметрией. Модулярные формы и эллиптические кривые обитают в совершенно различных областях математического мира, и никому и в голову не приходило, что между ними существует какая-нибудь связь. Поэтому Танияма и Шимура повергли математическое сообщество в состояние шока своей гипотезой о том, что эллиптические кривые и модулярные формы по существу представляют собой одно и то же.