ЗАДАЧА № 71 Горизонт Часто
приходится читать и слышать, что одно из убедительных доказательств
шарообразности земли – круглый вид горизонта. Так как всюду линия
горизонта – окружность, то земля наша должна быть шаром. Подумайте,
однако: какую фигуру имела бы линия горизонта, если бы земля наша была
не шарообразная, а плоская, бесконечно простираясь во все стороны? ЗАДАЧА № 72 Где и когда? Вам, вероятно, знаком бессмысленный стишок Рано утром, вечерком, В полдень, на рассвете…
Неведомый слагатель этих стихов стремился выразить ими заведомую нелепость и подбирал слова, одно другому противоречие. Между
тем приведенная фраза не совсем бессмысленна; существуют места на
земле, где такое определение времени вполне применимо и относится к
некоторому реальному моменту. Где же и когда это бывает? ЗАДАЧА № 73 Рост Эзопа
«Уверяют,
что Эзопова голова была длиною 7 дюймов, а ноги так длинны, как голова и
половина туловища; туловище ж равно длине ног с головою. Спрашивается рост сего славного человека». ЗАДАЧА № 74 Пять обрывков цепи Кузнецу
принесли пять цепей, по три звена в каждой – они изображены здесь на
рисунке (черт. 58) – и поручили соединить их в одну цепь. 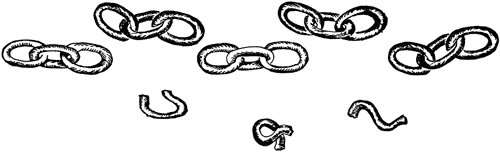
Рис. 58. Обрывки цепи. Прежде
чем приняться за дело, кузнец стал думать о том, сколько колец
понадобится для этого раскрыть и вновь заковать. Он решил, что придется
раскрыть и снова заковать четыре кольца. Нельзя ли, однако, выполнить ту же работу, раскрыв меньше колец? ЗАДАЧА № 75
Четырьмя пятерками Нужно выразить число 16 с помощью 4 пятерок, соединяя их знаками действий. Как это сделать? ЗАДАЧА № 76
Вишня Мякоть
вишни окружает ее косточку слоем такой же толщины, как и сама косточка.
Будем считать, что и вишня и косточка имеют форму шариков. Можете ли вы
сообразить в уме, во сколько раз объем сочной части вишни больше объема
косточки? ЗАДАЧА № 77
Дыни Продаются две дыни. Одна, окружностью 72 сантиметра, стоит 40 рублей. Другая, окружностью 60 сантиметров, стоит 25 рублей. Какую дыню выгоднее купить? ЗАДАЧА № 78
Удивительная затычка В
доске выпилены три отверстия: одно – квадратное, другое – круглое,
третье – в форме креста. На нашем чертеже 59-м вы видите эти отверстия. 
Рис. 59. Заткнуть эти отверстия одной и той же затычкой. Нужно изготовить затычку такого фасона, чтобы она годилась для каждого из этих отверстий. Вам кажется, что такой всеобщей затычки быть не может: отверстия чересчур разнообразны по форме. Могу вас уверить, что подобная затычка существует. Попытайтесь найти ее. ЗАДАЧА № 79
Модель башни Эйфеля Башня
Эйфеля в Париже, 300 метров высоты, сделана целиком из железа, которого
пошло на нее 8000000 килограммов. У моего знакомого есть точная модель
знаменитой башни, весящая всего только один килограмм. Какой она высоты? Выше стакана или ниже? ЗАДАЧА № 80
Муха на ленте У
меня была в руках длинная бумажная лента, с одной стороны красная, с
другой – белая. Я склеил ее концы и получившееся бумажное кольцо положил
на стол. Внимание мое привлекла муха,
севшая на красную сторону ленты и начавшая странствовать по ней. Я стал
следить за ее путешествием вдоль ленты и, к изумлению, заметил, что,
побродив немного по ленте, она очутилась на противоположной, белой
стороне, хотя все время оставалась на ленте и нигде не переползала через
ее край. Продолжая следить за ее движениями, я вскоре увидел ее снова
на красной стороне ленты, хотя положительно мог утверждать, что она не
переступала и не перелетала через края ленты и ползла все время, не
покидая ее. Не объясните ли вы, как могло это случиться? РЕШЕНИЯ ЗАДАЧ №№ 71-80 Решение задачи № 71 Если бы земля была совершенно плоская, линия горизонта и в таком случае была бы окружностью! Действительно:
что такое горизонт? Линия, по которой небесный свод кажущимся образом
встречается с землей. Но свод небесный имеет форму шаровой поверхности.
По какой же другой линии может пересекаться шаровая поверхность с
плоскостью, как не по окружности? Итак, круглая форма горизонта сама по себе не доказывает еще, что земля кругла! Решение задачи № 72 Где? За полярным кругом. Когда?
Около 21-го декабря, когда зимнее солнце лишь на мгновение показывается
верхним краем из-под горизонта в 12 часов дня, чтобы тотчас же скрыться
снова под горизонт. Действительно.
Этот момент есть «утро», так как совпадает с восходом солнца; но он в то
же время и вечер, так как совпадает с заходом солнца. Это безусловно
полдень – 12 часов дня, и, конечно, рассвет, так как, пока солнце еще не
вынырнуло из-под горизонта, длится утренняя заря. Итак, это – «рано
утром, вечерком, в полдень, на рассвете». Решение задачи № 73 Мы
знаем из условия задачи, что ноги Езопа равны 7 дюймам (голова) + длина
половины туловища. Известно еще, что туловище = длине ног + 7 дюймов,
откуда длина ног = туловищу без 7 д. Итак, ноги Езопа = длине половины
туловища + 7 дюймов, и в то же время = туловищу без 7 дюймов. Значит 1/2 туловища + 7 д. = туловищу – 7 д., или:
туловище длиннее 1/2 туловища на 14 д., откуда 1/2 туловища = 14 дюйм.,
а все туловище = 28 дюйм. Прибавив длину головы и ног (которые вместе =
туловищу, т. е. 28 д.), получаем рост Езопа: 56 дюймов, или 2 аршина. Решение задачи № 74 Достаточно разогнуть только три кольца одного из обрывков и полученными кольцами соединить концы остальных четырех обрывков. Решение задачи № 75 Существует только один способ: 55/5 + 5 = 16. Решение задачи № 76 Толщина
слоя мякоти равна поперечнику косточки, – значит, поперечник вишни в 3
раза больше поперечника косточки. Отсюда объем вишни больше объема
косточки в 3x3x3 = 27 раз. И, следовательно, объем мякоти больше объема
косточки в 27-1 = 26 раз. Решение задачи № 77 Окружность
большой дыни (72 см) превышает окружность меньшей (60 см) в 24/20,
т. е. в 1 1/5 раза. Таково же и отношение ее поперечника к поперечнику
меньшей дыни. Ее объем больше в 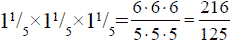
раз.
Если меньшая дыня стоит 25 рублей, то большая должна стоить 25 x
216/125 = 216/5 = 43 р. 20 к. Между тем дыня стоит всего 40 рублей.
Ясно, что ее купить выгоднее, чем меньшую.Решение задачи № 78 Искомая
затычка имеет форму, изображенную здесь на чертеже 60-м. Вы можете
заткнуть ею и квадратное отверстие, и круглое, и крестообразное. 
Рис. 60. Решение задачи № 79 Модель
весом 1 килограмм гораздо выше стакана, потому что – как это ни
неожиданно, – она имеет в высоту 1 1/2 метра! В самом деле: модель
меньше самой башни по объему во столько раз, во сколько 1 килограмм
меньше 8000000 килограммов, т. е. в 8000000 раз. Значит, высота модели
меньше высоты башни в такое число раз, которое, будучи дважды умножено
на себя, составит 8000000; число это 200, потому что 200x200x200 =
8000000. Разделив высоту Эйфелевой башни, 300 метров, на 200, получаем 1
1/2 метра (около двух аршин). Результат довольно странный. 1
1/2-метровое железное изделие весит всего 1килограмм! Это объясняется
тем, что Эйфелева башня – сооружение, при своих больших размерах,
необыкновенно легкое, как говорят – «ажурное». Решение задачи № 80 Загадка
объясняется тем, что один конец ленты, прежде чем его приклеили к
другому, был повернут один раз. Легко убедиться на опыте, что тогда
получается кольцо, ползая по которому, муха может обойти обе его
стороны, нигде не переступая через края. 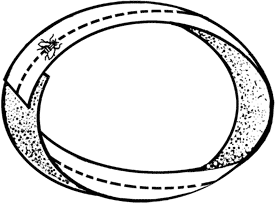
| 
