ЗАДАЧА № 21 Сколько прямоугольников? Сколько прямоугольников можете вы насчитать в этой фигуре? Не
спешите с ответом. Обратите внимание на то, что спрашивается не о числе
квадратов, а о числе прямоугольников вообще – больших и малых, – какие
можно насчитать в этой фигуре. 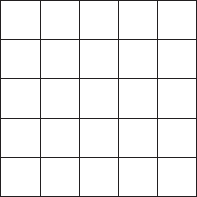
Рис. 21. ЗАДАЧА № 22
Реомюр и Цельсий Вы
знаете, конечно, разницу между термометрами Реомюра и Цельсия. Скажите
же: всегда ли градусы на термометре Реомюра больше, чем градусы на
термометре Цельсия? 
Рис. 22. ЗАДАЧА № 23
Столяр и плотники Шесть
плотников и столяр нанялись на работу. Каждый плотник заработал по
20 руб., столяр же – на 3 руб. больше, чем заработал, в среднем, каждый
из семерых. Сколько же заработал столяр? ЗАДАЧА № 24
Девять цифр Напишите по порядку девять цифр: 1 2 3 4 5 6 7 8 9. Вы можете, не меняя их порядка, вставить между цифрами знаки плюс и минус таким образом, чтобы в сумме получилось ровно 100. Нетрудно, например, вставив + и – шесть раз, получить 100 таким путем: 12+3–4+5+67+8+9 = 100. Если хотите вставить + или – всего только 4 раза, вы тоже можете получить 100. 123+4–5+67–89 = 100. Попробуйте, однако, получить 100, пользуясь знаками + и – всего только три раза! Это гораздо труднее. И все же – вполне возможно, надо только терпеливо искать. ЗАДАЧА № 25
Книжный червь В моем книжном шкафу стоят на полке сочинения Пушкина в 8-ми томах, том к тому. Приехав
с дачи, я с досадой убедился, что летом книжный червь усердно сверлил
моего Пушкина и успел прогрызть ход от первой страницы первого тома до
последней страницы третьего тома. Сколько всего страниц прогрыз червь, если в первом томе 700 страниц, во втором – 640, а в третьем – 670? ЗАДАЧА № 26
Сложение и умножение Вы, без сомнения, не раз уже обращали внимание на любопытную особенность равенств: 2+2 = 4 2x2 = 4. Это
единственный пример, когда сумма и произведение двух целых чисел (и при
том равных) одинаковы. Вам, однако, быть может, неизвестно, что
существуют дробные числа (правда, не равные), обладающие тем же
свойством: 3+1 1/2 = 4 1/2 3x1 1/2 = 4 1/2, Попытайтесь
подыскать еще примеры таких же чисел. Чтобы вы не думали, что поиски
напрасны, скажу вам, что таких чисел весьма-весьма много. ЗАДАЧА № 27
Стрельба на пароходе Хороший
стрелок стоит у одного борта парохода, а у противоположного помещена
мишень. Пароход движется так, как изображено длинной стрелкой на
приложенном здесь чертеже. 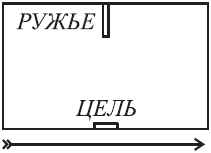
Рис. 23. Стрелок прицелился совершенно точно. Попадет ли он и цель? ЗАДАЧА № 28
Под водой На
обыкновенных весах лежат: на одной чашке – булыжник, весящий ровно 2
килограмма, на другой – железная гиря в 2 килограмма. Я осторожно
опустил эти весы под воду. Остались ли чашки в равновесии? ЗАДАЧА № 29
Как это сделано Вы
видите здесь деревянный куб, сделанный из двух кусков дерева: верхняя
половина куба имеет выступы, входящие в выемки нижней части. Но обратите
внимание на форму и расположение выступов и объясните: как ухитрился
столяр соединить оба куска? 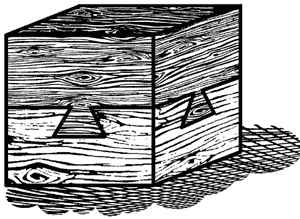
Рис. 24. ЗАДАЧА № 30
Cкорость поезда Вы сидите в вагоне железной дороги и желаете узнать, с какою скоростью он мчится. Можете ли вы это определить по стуку колес? РЕШЕНИЯ ЗАДАЧ №№ 21-30 Решение задачи № 21 Различно расположенных прямоугольников в этой фигуре можно насчитать 225. Решение задачи № 22 Если
бы речь шла о градусах температуры, то, конечно, градус Реомюра всегда
больше градуса Цельсия, именно на 1/5 долю; поэтому, если в вашей
комнате 16 градусов Реомюра, то по Цельсию – 20. Но
это вовсе не значит, что на той дощечке термометра, на которой нанесены
деления (на «шкале»), длина градусов всегда должна быть больше у
термометра Реомюра, нежели у Цельсия. Длина деления зависит от того,
сколько ртути в шарике термометра, и от толщины трубки. Чем больше ртути
в шарике и чем тоньше канал трубки, тем выше поднимается ртуть в трубке
при нагревании и тем больше промежуток между двумя делениями шкалы. В
этом смысле «градус» может иметь самую различную длину, и вполне
понятно, что такой градус Реомюра бывает нередко меньше градуса Цельсия. Решение задачи № 23 Легко
узнать, каков был средний заработок семерых рабочих; для этого нужно
избыточные 3 рубля разделить поровну между 6 плотниками. К 20 рублям
каждого надо, следовательно, прибавить 50 коп., – это и есть средний
заработок каждого из семерых. Отсюда узнаем, что столяр заработал 20 р. 50 к. + 3 р., т. е. 23 р. 50 к. Решение задачи № 24 Вот каким способом можете вы получить 100 из ряда девяти цифр и трех знаков + и —: 123-45-67+89 = 100. В самом деле: 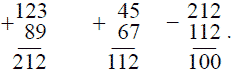
Других решений задача не имеет. Впрочем, если у вас есть терпение, попытайтесь испробовать другие сочетания. Решение задачи № 25 Казалось
бы, надо просто сложить числа страниц трех томов – и задача решена. Но
не спешите с решением. Обратите внимание на то, как стоят книги на полке
и как расположены в них страницы. 
Рис. 25. Вы
видите, что 1-я страница I тома примыкает к 640-й странице II тома, а
последняя страница III находится рядом с первой страницей II тома. И
если червь проделал ход от 1-й страницы 1 тома до последней страницы
III тома, то он прогрыз всего только 640 страниц среднего тома, да еще 4
крышки переплета, – не более. Решение задачи № 26 Существует б е с ч и с л е н н о е м н о ж е с т в о пар таких чисел. Вот несколько примеров: 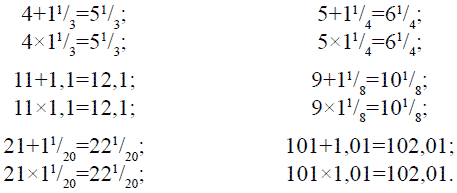
Решение задачи № 27 Конечно,
меткий стрелок попадет в цель, – если только пароход движется
равномерно по прямой линии. Такое движение парохода ничем не может
повлиять на полет пули. Другое дело,
если бы в самый момент выстрела пароход внезапно остановился, или
замедлил ход, или ускорил его, или изменил курс: тогда пуля могла бы и
не попасть в цель. Решение задачи № 28 Каждое
тело, если погрузить его в воду, становится легче: оно «теряет» в своем
весе столько, сколько весит вытесненная им вода. Зная этот закон
(открытый Архимедом), мы без труда можем ответить на вопрос задачи. Булыжник
весом в 2 килограмма занимает больший объем, чем 2-килограммовая
железная гиря, потому что материал камня, гранит, легче железа. Значит,
булыжник вытеснит больший объем воды, нежели гиря, и, по закону
Архимеда, потеряет в воде больше веса, чем гиря: носы под водой
наклонятся в сторону гири. Решение задачи № 29 Ларчик открывается очень просто, как видно из чертежа 26-го. 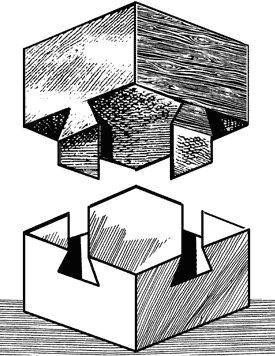
Рис. 26. Все
дело только в том, что выступы и углубления идут не крестом, как
невольно кажется при рассматривании готовой вещи, а параллельно, в косом
направлении. Такие выступы очень легко сбоку вдвинуть в соответствующие
выемки. Решение задачи № 30 Вы
заметили, конечно, что при езде в вагоне все время ощущаются мерные
толчки; никакие рессоры не могут сделать их неощутительными. Толчки эти
происходят оттого, что колеса слегка сотрясаются в местах соединения
двух рельсов, и этот толчок передается всему вагону. Значит, стоит лишь
вам сосчитать, сколько толчков в минуту испытывает вагон, чтобы узнать,
сколько рельсов пробежал поезд. Теперь остается лишь умножить это число
на длину рельса, – и вы получите расстояние, проходимое поездом в одну
минуту. 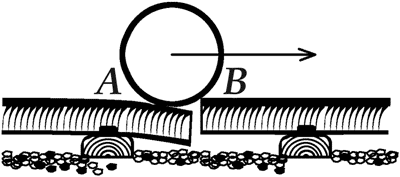
Рис. 27.
Когда железнодорожное колесо проходит через место соединения рельсов,
конец А отгибается вниз, между тем как конец В еще остается прямым.
Отсюда толчок, который ощущают едущие в вагоне. Обычная
длина рельса – около 8 1/2 метров [3] . Сосчитав с часами в руках число
толчков в минуту, умножьте это число на 8 1 / затем на 60 и делите на
1000– получится число километров, пробегаемое поездом в час: 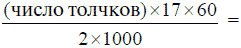 числу километров в час. числу километров в час.
Так как 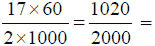 около
половины, то достаточно просто разделить на 2 число толчков в минуту,
чтобы приблизительно узнать, сколько километров пробегает поезд в час.
| 
