ЗАДАЧА № 61 Дешевый сторож Арендатору
большого фруктового сада понадобилось на целые сутки отлучиться как раз
в ту пору, когда яблоки поспели и представляли наибольший соблазн для
любителей полакомиться на чужой счет. Необходимо было нанять на эти
сутки сторожа. Скупой арендатор долго выбирал сторожа подешевле, пока не
напал на такого, который вовсе не просил денег, а довольствовался
уплатой яблоками. Это понравилось арендатору. – Понадобится сторожить целые сутки без смены и перерыва, никуда не отлучаясь. Поспать успеете потом, когда отдежурите. – Хорошо, буду без смены. Но платить вам придется не ровно: за каждый следующий час вдвое против предыдущего. – Это бы можно; но сколько же вы хотите за первый час? – Уж
чего меньше: одно яблоко за первый час дадите, и достаточно. За второй –
два яблока положите, и довольно. За третий – четыре, и хватит. За
четвертый… – Ладно, – поспешил
согласиться арендатор. – «Если этот чудак так же честен, как
нерасчетлив, то я, кажется, сделал выгодное дело: за несколько десятков
яблок достал сторожа на целые сутки», – подумал он, уходя. Сторож был нанят, и арендатор спокойно уехал, радуясь тому, что на свете есть люди, не умеющие считать. Когда,
спустя сутки, арендатор возвратился к своему саду, он увидел у ворот
телегу, на которую его сторож ссыпал один мешок яблок за другим. – Это что такое! – накинулся на него арендатор. – Я нанимал вас сторожить, а не грабить. Куда увозите мои яблоки? – Были ваши, теперь мои, – спокойно ответил сторож. – Забыли, небось, уговор? – Уговор? Да разве по нашему уговору вам за одни сутки следует яблок целый воз? Считать не умеете… – И не один воз следует. Сами считать не умеете. – Не один воз! Что за вздор! Уж не все ли яблоки моего сада? – Не только вашего. Во всем городе не закупите яблок, чтобы со мной расплатиться. Возов тысячи три понадобится, не меньше. – Три тысячи возов яблок? За одни сутки? Ничего не понимаю… А вы, читатель, понимаете? Кто из них считать не умел: сторож или арендатор? А может быть, ни тот ни другой? ЗАДАЧА № 62 Крестьянка и паровоз Железнодорожный
машинист задолжал крестьянке за молоко и уклонялся от платежа.
Молочница долго ждала и наконец придумала, что делать. Однажды, когда пары были уже разведены и поезд должен был тронуться, она стала у паровоза и заявила машинисту: – Отдавай сейчас долг, иначе не пущу поезда! Машинист, разумеется, только усмехнулся, услыхав такую угрозу. Но женщина не шутя намеревалась остановить поезд. И что же? Машинист пустил в ход машину, но паровоз ни с места. Машина работает, а поезд стоит, словно заколдованный. – Отдай деньги – пущу поезд! – с торжеством объявила крестьянка. Пришлось машинисту заплатить долг полностью; тогда только поезд тронулся. В чем же состояло «колдовство» молочницы, и как оно было ею снято? ЗАДАЧА № 63 Путешествие шмеля Шмель
отправляется в дальнее путешествие. Из родного гнезда он летит прямо на
юг, пересекает речку и наконец, после целого часа пути, спускается на
косогор, покрытый душистым клевером. Здесь, перелетая с цветка на
цветок, шмель остается полчаса. Теперь
надо посетить сад, где шмель вчера заметил цветущие кусты крыжовника.
Сад лежит на запад от косогора, и шмель спешит прямо туда. Спустя 3/4
часа он был уже в саду. Крыжовник в полном цвету, и, чтобы посетить все
кусты, понадобилось шмелю полтора часа. А затем, не отвлекаясь в стороны, шмель кратчайшей дорогой полетел домой, в родное гнездо. Сколько времени шмель пробыл в отсутствии? ЗАДАЧА № 64 Ящик У
меня есть ящичек, и я могу вам сказать, что крышка его заключает 120
квадратных дюймов, передняя стенка – 96 кв. дюймов и боковая – 80 кв.
дюймов. 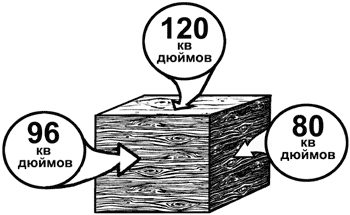
Рис. 65. Можете ли вы определить, каковы размеры моего ящичка, т. е. сколько он имеет в длину, ширину и высоту?
ЗАДАЧА № 65
Две цепи Найдены
два обрывка железной цепи, составленные из одинаковых звеньев. Один
обрывок, будучи растянут, занимает в длину 36 сантиметров, другой – 22
сантиметра. Толщина кольца – полсантиметра. В длинной цепи на 6 звеньев
больше, чем в короткой. Сколько звеньев в каждом обрывке? ЗАДАЧА № 66
Мешки с мукой Мельнику
надо было взвесить 5 мешков с мукой. У него были весы, но не хватало
некоторых гирь, и невозможно было отвесить груз меньше, чем 100
килограммов. Мешки же весили около 60 килограммов каждый. Мельник
не растерялся и стал взвешивать мешки по два, парами. Из 5 мешков можно
составить 10 различных пар; поэтому пришлось сделать 10 взвешиваний.
Получился ряд чисел, который приведен здесь в возрастающем порядке: 110 кг, 112 кг, 113 кг, 114 кг, 115 кг, 116 кг, 117 кг, 118 кг, 120 кг и 121 кг. Но сколько же весит каждый мешок в отдельности? Как это узнать? Мельник справился с этой задачей довольно быстро. Вероятно, и вы догадаетесь, как она решается. ЗАДАЧА № 67
Три дочери и два сына Дядя приехал навестить своих двух племянников и трех племянниц, которых не видал уже давно. Первыми вышли к нему маленький Володя с сестренкой Женей, и мальчуган гордо объявил дяде, что он в два раза старше своей сестры. Затем выбежала Надя, и вошедший с нею папа сказал гостю, что обе девочки вместе вдвое старше мальчика. Когда пришел из школы Алеша, папа объявил, что оба мальчика вместе вдвое старше обеих девочек вместе. Позднее всех пришла Лида и, увидя гостя, радостно воскликнула: – Дядя, вы приехали как раз в день моего рождения! Мне сегодня исполнился 21 год! – И знаете еще что, – прибавил отец, – я сейчас сообразил, что мои три дочери вместе вдвое старше обоих моих сыновей. Сколько же лет было каждому сыну и каждой дочери? ЗАДАЧА № 68
Две свечи Внезапно
погас электрический свет во всей квартире – испортились провода. Чтобы
не прерывать работы, я зажег две свечи, стоявшие, на всякий случай, на
моем письменном столе, и при их свете занимался до тех пор, пока
проводка не была приведена в исправность. Спустя
день мне понадобилось узнать, на сколько именно времени было прервано
электрическое освещение. Я забыл отметить по часам момент прекращения
тока и момент его возобновления. Не помнил я и длины свеч. Знаю только,
что одна свеча была потолще, – из тех, что сгорают целиком в 5 часов;
другая была потоньше и могла бы сгореть в 4 часа. Ищу огарки – и не
нахожу: домашние выбросили их. – Какой же они были длины? – спрашиваю у них. – Один был совсем маленький, а другой побольше. – Во сколько же раз больше? Вдвое?.. Не помните ли этого? – допытывался я. – Ровно в четыре раза, – получил я ответ. Итак,
я узнал только то, что один огарок был в 4 раза длиннее другого.
Возможно ли на этом основании определить, сколько времени горели свечи? ЗАДАЧА № 69
Девятьсот поклонов В
одной школе обучалось вдвое больше девочек, чем мальчиков. Заведующий
ввел обычай, чтобы ежедневно поутру каждый мальчик делал поклон
заведующему, каждому из своих товарищей-мальчиков и каждой девочке;
каждая девочка тоже должна была делать поклон заведующему, каждой
подруге и каждому мальчику. Этот церемонный обычай строго соблюдался, и поэтому ежедневно утром можно было насчитать 900 поклонов. Сколько было в школе мальчиков и девочек? ЗАДАЧА № 70
Наследство раджи Некий
раджа, умирая, оставил свои брильянты сыновьям. Завещание было
составлено так: старший сын получает 1 брильянт и седьмую долю всех
остальных; второй сын получает 2 брильянта и седьмую долю всех
остальных; третий сын получает 3 брильянта и седьмую долю всех
остальных; четвертый – 4 брильянта и седьмую долю остальных. И т. д.
Таким образом наследство было разделено между сыновьями без остатка. Сколько сыновей было у раджи, и сколько он оставил брильянтов? РЕШЕНИЯ ЗАДАЧ №№ 61-70 Решение задачи № 61 Сторож рассчитал совершенно правильно: ему действительно следовало даже более трех тысяч возов яблок, – как это ни невероятно. В самом деле. Проследим, как возрастало вознаграждение сторожа с каждым часом. За
1-й час сторожу следовало 1 яблоко, за 2-й час – 2 яблока, за 3-й – 4
яблока, за 4-й – 8, за 5-й – 16, за 6-й – 32, за 7-й – 64, за 8-й – 128,
за 9-й – 256, за 10-й – 512. Пока еще
вознаграждение как будто не грозит арендатору разорением: за первые 10
часов сторожу причиталось всего около тысячи яблок. Но будем продолжать исчисление. За 11-й час сторожу следовало 1024 яблока, за 12-й – 2048, за 13-й – 4096, за 14-й – 8192, за 15-й – 16384. Число яблок накопляется внушительное, но все же это далеко от трех тысяч возов. Дальше. За 16-й час уже следовало 32768 яблок. За 17-й час следовало 65536 яблок. За 18-й час следовало 131072 яблок. За 19-й час следовало 262144 яблок. За 20-й час следовало 524288 яблок. Арендатор уже должен сторожу свыше миллиона яблок. Но сутки не копчены – остается еще 4 часа. За 21-й час надо было уплатить 1048576 яблок. За 22-й час следовало 2097152 яблок. За 23-й час следовало 4194304 яблок. За 24-й час следовало 8388608 яблок. Теперь
остается сложить все эти числа от 1 до 8388608. Составится 16777215
яблок. Итак, сторожу за одни сутки следовало, согласно уговору, почти 17
миллионов яблок! Чтобы только пересчитать такое число яблок по одному в
секунду, понадобилось бы полгода непрерывного счета! Полагая по 10
яблок на килограмм, получаем, что все причитающиеся сторожу яблоки
должны были весить 1677721 килограмм, или 1677 тонн. Это составило бы вагонов 80, груженных яблоками, или – считая по полтонны на воз – свыше 3000 возов. Не правда ли, можно было найти сторожа и подешевле? Решение задачи № 62 Крестьянка
остановила поезд тем, что смазала маслом рельсы впереди паровоза. По
скользким рельсам не могут катиться колеса паровоза; они вертятся на
одном месте, но не катятся вперед, так как нет трения, благодаря
которому колеса словно цепляются за рельсы. Вспомните, как трудно ходить
по гладкому льду: ноги скользят, не находя опоры, и мы не можем
сдвинуться с места. По той же причине не может сдвинуться и паровоз на
скользких рельсах. Когда же машинист уплатил долг, крестьянка «сняла колдовство», посыпав смазанные рельсы песком. История
эта, конечно, могла произойти только в давнее время; на современных
паровозах имеются особые песочницы, из которых машинист с помощью
особого приспособления высыпает песок на рельсы, когда они становятся
скользкими, например, от дождя. Решение задачи № 63 Задача
решалась бы очень просто, если бы было сказано, сколько времени
понадобилось шмелю на перелет из сада в родное гнездо. Этого в задаче не
сказано, – но геометрия поможет нам самим узнать это. 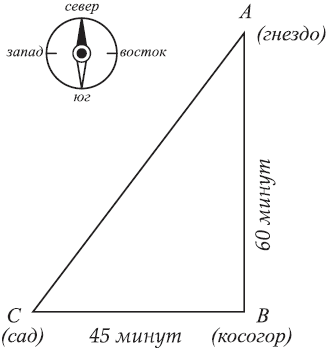
Рис. 66. Начертим
путь шмеля. Мы знаем, что шмель летел сначала «прямо на юг» в течение
60-ти минут. Затем он летел 45 минут «на запад», т. е. под прямым углом к
прежнему пути. Оттуда «кратчайшей дорогой», т. е. по прямой линии –
обратно к гнезду. У нас получился прямоугольный треугольник ABC, в
котором известны оба «катета», АВ и ВС, и надо определить третью сторону
– «гипотенузу» АС. Геометрия учит, что
если какая-нибудь величина содержится в одном катете 3 раза, а в другом
– 4 раза, то в третьей стороне – гипотенузе – та же величина должна
содержаться ровно пять раз. Например, если катеты треугольника равны 3 и
4 метрам, то гипотенуза = 5 м; если катеты 9 и 12 километров, то третья
сторона = 15 км и т. п. В нашем случае один катет 3x15 мин. пути,
другой – 4x15 мин. пути; значит, гипотенуза АС = 5x15 минут пути. Итак,
мы узнали, что из сада к гнезду шмель летел 75 минут, т. е. 1 1/4 часа. 
Рис. 67. Теперь легко уже подсчитать, сколько времени пробыл шмель в отсутствии. На перелеты он употребил времени: 1 час + 3/4 часа + 1 1/4часа = 3 часа. На остановки у него ушло времени: 1/2 часа + 1 1/2 часа = 2 часа. Итого: 3 часа + 2 часа = 5 часов. Решение задачи № 64 Поверхность
крышки равна произведению длины ящика на его ширину; поверхность
боковой стенки = высоте x ширину; поверхность передней стенки = высоте x
длину. Следовательно, мы знаем, что длина x ширину = 120 высота x ширину = 80 высота x длину = 96. Перемножим первые два равенства. Получим: длина x высоту x ширину x ширину = 120x80. Разделим это новое равенство на 3-е: 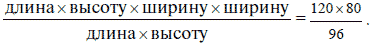
Сократив дробь и произведя действия, имеем: ширина x ширину = 100. И следовательно, ширина ящика = 10 см. Зная это, легко определить, что высота ящика = 80/10 = 8 см, а длина = 96/8 = 12 см. Решение задачи № 65 Вы не решите этой простой задачи, если не уясните себе сначала, из чего составляется длина цепи. Всмотритесь в чертеж: 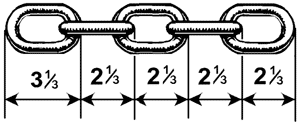
Рис. 68. Вы
видите, что длина натянутой цепи составляется из полной ширины первого
звена, к которой, с присоединением каждого нового звена, прибавляется не
полная ширина звена, а ширина без двойной толщины звена. Теперь перейдем к нашей задаче. Мы
знаем, что одна цепь длиннее другой на 14 сантиметров и имеет на 6
звеньев больше ее. Разделив 14 на 6, мы получаем 2 1/3. Это и есть
ширина одного звена, уменьшенная на двойную его толщину. Так как толщина
кольца известна – полсантиметра, – то, следовательно, полная ширина
каждого звена = 2 1/3 + 1/2 + 1/2 = 3 1/3 сантиметра. Теперь
легко определить, из скольких звеньев состояла каждая цепь. Из чертежа
видно, что если мы отнимем от 36-сантиметровой цепи двойную толщину
первого звена, т. е. 1сантиметр, и остальное разделим на 2 1/3, то
получим число звеньев в этой цепи: 35 : 2 1/3 = 15. Точно так же узнаем число звеньев в 22-сантиметровый цепи: 21 : 2 1/3 = 9. Решение задачи № 66 Мельник
начал с того, что сложил все 10 чисел. Полученная сумма, 1156
килограммов, – не что иное, как учетверенный вес мешков: ведь в нее вес
каждого мешка входит 4 раза. Разделив на 4, узнаем, что все пять мешков
вместе весят 289 килограммов. Теперь для
удобства обозначим мешки, в порядке их веса, номерами. Самый легкий
мешок – это № 1, второй по тяжести – № 2 и т. д.; самый тяжелый мешок –
№ 5. Нетрудно сообразить, что в ряде чисел: 110 кг, 112 кг, 113 кг,
114 кг, 115 кг, 116 кг, 117 кг, 118 кг, 120 кг, 121 кг – первое число
составилось из веса двух самых легких мешков: № 1 и № 2; второе число –
из веса № 1 и № 3. Последнее число составилось на веса двух самых
тяжелых мешков № 4 и № 5, а предпоследние – из № 3 и № 5. Итак: № 1 и № 2 вместе весят 110 кг № 1 и № 3 вместе весят 112 кг № 3 и № 5 вместе весят 120 кг № 4 и № 5 вместе весят 121 кг Легко
узнать, следовательно, сумму весов № 1, № 2, № 4 и № 5: она равна
110 кг + 121 кг = 231 кг. Вычтя это число из общей суммы веса всех
мешков (289 кг), получаем вес мешка № 3, именно – 58 килограммов. Дальше,
из суммы веса мешков № 1 и № 3, т. е. из 112, вычитаем известный уже
нам вес мешка № 3; получается вес мешка № 1: 112 кг – 58 кг = 54 кг. Точно
так же узнаем вес мешка № 2, вычтя 54 кг из 110 кг, т. е. из суммы веса
мешков № 1 к № 2. Получаем: вес мешка № 2 равен 110 кг – 54 кг = 56 кг. Из
суммы весов мешков № 3 и № 5, т. е. из 120 вычитаем вес мешка № 3,
который равен 58 кг; узнаем, что мешок № 5 весит 120 кг – 58 кг = 62 кг. Остается определить вес мешка № 4 из суммы № 4 и № 5, т. е. из 121 кг. Вычтя 62 из 121, узнаем, что мешок № 4 весит 59 кг. Итак, вот вес мешков: 54 кг, 56 кг, 58 кг, 59 кг, 62 кг. Решение задачи № 67 Мы
знаем, что Володя вдвое старше Жени, а Надя и Женя вместе вдвое старше
Володи. Значит, годы Нади и Жени вместе вчетверо больше, чем годы Жени.
Отсюда прямо следует, что Надя старше Жени в 3 раза. Далее,
мы знаем, что сумма лет Алеши и Володи вдвое больше суммы лет Нади и
Жени. Но возраст Володи есть удвоенный возраст Жени, а годы Нади и Жени
вместе есть учетверенный возраст Жени. Следовательно, годы Алеши +
удвоенный возраст Жени = 8-кратному возрасту Жени. То есть: Алеша старше Жени в 6 раз. Наконец, нам известно, что сумма возрастов Лиды, Нади и Жени равна сумме возрастов Володи и Алеши. Имея перед глазами табличку: Лиде – 21 год. Надя – в 3 раза старше Жени, Володя – в 2 раза старше Жени, Алеша
– в 6раз старше Жени, мы можем сказать, что 21 год + утроенный возраст
Жени + возраст Жени = 4-кратному возрасту Жени + 12-кратному возрасту
Жени. Или: 21 год + 4-кратный возраст Жени = 16-кратному возрасту Жени. Значит, 21 год = 12-кратному возрасту Жени и, следовательно, Жене 21/12 = 1 3/4 года. Теперь уже легко определить, что Володе 3 1/2 года, Наде – 5 1/4 и Алеше – 10 1/2 лет. Решение задачи № 68 Для
ясности нарисуем рядом две свечи – толстую, ко – торая может сгореть в 5
часов, и тонкую, которая может сгореть в 4 часа. Заштрихуем те части
обеих свечей, которые сгорали, огарки же оставим незаштрихованными.
Легко сообразить, что длина сгоревшей части тонкой свечи должна
составлять 5/4 длины сгоревшей части толстой свечи; другими словами,
заштрихованный избыток тонкой свечи составляет по длине 1/4 сгоревшей
части толстой свечи. Но в то же время длина этого избытка = 3/4 длины
толстого огарка. Другими словами, мы узнали, что 3/4 длины толстого
огарка равна 1/4 длины сгоревшей части толстой свечи. Значит, 4/4 его
(т. е. весь огарок) составляет 1/4 x 4/3 = 1/3 толстой свечи. Итак,
огарок толстой свечи составляет 1/3 сгоревшей части или 1/4 всей длины
свечи. Сгорело, следовательно, 3/4 толстой свечи. А так как вся свеча
могла сгореть в 5 часов, то 3/4 ее горело в продолжение (5x3)/4 = 15/4 =
3 3/4 часа. Ответ: свечи горели 3 3/4 часа. Решение задачи № 69 Каждый
ученик или ученица ежедневно раскланивались со всеми остальными
школьниками и с заведующим. С самим собою, конечно, не раскланивались,
зато делали поклон заведующему, так что каждый школьник и школьница
делали ежедневно столько поклонов, сколько было детей в школе. Значит,
все дети вместе делали ежедневно столько поклонов, сколько составится от
умножения их общего числа самого на себя. Итак,
мы знаем, что 900 – это число детей, умноженное само на себя. Какое же
число, умноженное на себя, составит 900? Очевидно, 30. А так как девочек
было вдвое больше, чем мальчиков, то из 30 детей было 20 девочек и
10мальчиков. Проверим это. Девочки
делают подругам 19x20 = 380 поклонов и мальчикам 20x10 = 200 поклонов.
Мальчики мальчикам 9x10 = 90, девочкам 10x20 = 200. Итого 380+200+90+200
= 870 поклонов. Присоединив еще 30 поклонов заведующему, имеем ровно
900. Решение задачи № 70 Задачу надо
решать с конца. Самый младший сын получил столько брильянтов, сколько
было сыновей, и еще 1/7 остальных; но так как остатка никакого не было,
то младший сын получил столько брильянтов, сколько было всех сыновей.
Далее: предыдущий сын получил брильянтов на один меньше, чем было
сыновей, да еще 1/7 остальных брильянтов. Значит, то, что получил самый
младший, есть 6 седьмых долей этого «остального» (а все «остальное» есть
7 седьмых). Отсюда вытекает, что число
брильянтов самого младшего сына должно делиться на 6 без остатка.
Попробуем допустить, что их было 6, и испытаем, подходит ли это число. Если
младший сын получил 6 брильянтов, то, значит, он был шестой сын, и всех
сыновей было 6. Пятый сын получил 5 брильянтов + 1/7 от 7, т. е. 5+1 =
6. Далее: 12 камней есть 6/7 оставшегося после четвертого сына; полный
остаток – 14 камней, и четвертый сын получил 4+1/7 от 14 = 6. Вычисляем
остаток после третьего сына: 18 есть 6/7 этого остатка: значит, полный
остаток – 21. На долю третьего сына досталось 3+1/7 от 21 = 6. Точно так же узнаем, что на долю второго и первого сына досталось тоже по 6 камней. Итак, у раджи было 36 брильянтов и 6 сыновей. Мы
испытали число 6 и нашли, что оно удовлетворяет условиям задачи.
Испытав 12, 18 и 24, убедимся, что эти числа не годятся, а больше двух
дюжин детей у раджи едва ли могло быть.
| 
