ЗАДАЧА № 81

Кто больше?

Двое человек считали в течение часа всех прохожих, которые проходили мимо них на тротуаре. Один из считавших стоял у ворот дома, другой прохаживался туда и назад по тротуару.

Кто насчитал больше прохожих?

ЗАДАЧА № 82

Возраст моего сына

Теперь мой сын моложе меня втрое. Но пять лет назад он был моложе меня в четыре раза.

Сколько ему лет?

ЗАДАЧА № 83

Состязание

Две парусные лодки участвуют в состязании: требуется пройти 24 версты туда и назад в кратчайшее время. Первая лодка прошла весь путь с равномерной скоростью 20 верст в час; вторая двигалась туда со скоростью 16 верст в час, а обратно – со скоростью 24 версты в час.

Победила на состязании первая лодка, – хотя, казалось бы, вторая должна была на пути в одном направлении отстать от первой ровно на столько же, на сколько она опережала ее на обратном пути, и, следовательно, прийти одновременно с первой. Почему же она опоздала?

ЗАДАЧА № 84

По реке и по озеру

Плывя вниз по реке, гребец проплывает 5-верстное расстояние в 10 минут. Возвращаясь, он проплывает то же расстояние в час. Следовательно, 10 верст он, при указанных условиях, проплывает в 1 час 10 минут.

А во сколько времени проплыл бы он 10 верст в стоячей воде озера?

ЗАДАЧА № 85

От Энска до Иксограда

Плывя по течению, пароход делает 20 верст в час; плывя против течения – всего 15 верст в час. Чтобы пройти от пристани гор. Энска до пристани гор. Иксограда, он употребляет на 5 часов меньше, чем на обратный путь.

Как далеко от Энска до Иксограда?

ЗАДАЧА № 86

Всмятку и вкрутую

Хозяйка сварила 5 яиц: два вкрутую и три всмятку. Но она забыла отметить, какие именно яйца сварены вкрутую и какие – всмятку, и подала их к столу на одном блюде.

Вы наудачу берете с блюда два яйца. Есть ли вам расчет биться об заклад, ставя один рубль против пяти, что вам попадутся оба крутых яйца?

ЗАДАЧА № 87

Игральная кость

Вот игральная кость (черт. 62): кубик с обозначенными на его гранях очками от 1 до 6. Петр бьется об заклад, что если бросить кубик 4 раза подряд, то за все четыре раза кубик непременно упадет один раз единичным очком кверху.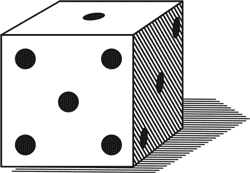

Рис. 62.

Владимир же ставит против него: он утверждает, что единичное очко либо совсем не выпадет при четырех метаниях, либо же выпадет больше одного раза. У кого из них больше вероятия выиграть?

ЗАДАЧА № 88

Семеро друзей

У одного гражданина было 7 друзей. Первый посещал его каждый вечер, второй – каждый второй вечер, третий – каждый третий вечер, четвертый – каждый четвертый вечер и т. д. до седьмого друга, который являлся каждый седьмой вечер.

Часто ли случалось, что все семеро друзей собирались у хозяина в один и тот же вечер?

В те вечера, когда семеро друзей собирались вместе, хозяин угощал их вином, и все чокались друг с другом попарно.

Сколько раз звучали при этом стаканы, сталкиваясь между собою?

Об основании древнего города Карфагена существует следующее предание. Дидона, дочь тирского царя, потеряв мужа, убитого рукой ее брата, бежала в Африку и высадилась со многими жителями Тира на ее северном берегу. Здесь она купила у нумидийского царя столько земли, «сколько занимает воловья шкура». Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и, благодаря такой уловке, охватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, к которой впоследствии был пристроен город.

Попробуйте вычислить, какую площадь могла, согласно этому преданию, занимать крепость, если считать, что воловья шкура имеет поверхность 4 кв. метра, а ширину ремешков, на которые Дидона ее изрезала, принять равной одному миллиметру.

РЕШЕНИЯ ЗАДАЧ №№ 81-90

Оба насчитали одинаковое число прохожих. Действительно, хотя тот, кто стоял у ворот, считал проходивших в обе стороны, но тот, кто ходил, видел зато вдвое больше встречных людей.

Если сын теперь втрое моложе отца, то отец старше его на двойной его возраст. Пять лет назад отец был также, конечно, старше сына на двойной нынешний возраст сына. С другой стороны, так как тогда отец был старше сына в 4 раза, то он был старше его на тройной его тогдашний возраст. Следовательно, двойной нынешний возраст сына равен тройному прежнему возрасту его, или – что то же самое, – сын теперь в 1 1/2 раза старше, чем был 5 лет назад. Отсюда легко сообразить, что 5 лет – это половина прежнего возраста сына; и, значит, пять лет назад сыну было 10 лет, а теперь ему 15 лет.

Итак, сыну теперь 15 лет, отцу 45. Действительно: пять лет назад отцу было 40 лет, а сыну 10, т. е. вчетверо меньше.

Вторая лодка опоздала потому, что двигалась с 24-верстной скоростью меньшее время, чем с 16-верстной. Действительно, с 24-верстною скоростью она двигалась 24/24 = 1 час, а с 16-верстною 24/16 = 1 1/2часа. Поэтому она на пути туда потеряла времени больше, чем выгадала на обратном пути.

По течению гребец плывет со скоростью полверсты в минуту, против течения – со скоростью 1/12 версты. В первую скорость включена скорость самого течения, от второй она отнята. Следовательно, 1/2 + 1/12, т. е. 7/12 версты, деленное пополам (7/24 в.) – это истинная скорость самого гребца.

И, значит, в стоячей воде гребец пройдет 10 верст в

10 : 7/24 = 34 2/7 минуты.

Обычный же ответ – что в озере гребец проплывет 10 верст в то же время, как и в реке, так как потеря скорости будто бы восполняется выигрышем ее – совершенно не верен (см. предыдущую задачу).

Плывя по течению, пароход делает 1 версту в 3 минуты; плывя против течения – 1 версту в 4 минуты. На каждой версте пароход в первом случае выгадывает 1 минуту. А так как на всем расстоянии он выгадывает во времени 5 часов, или 300 минут, то, следовательно, от Энска до Иксограда 300 верст.

Действительно:

300/15 – 300/20 = 20 – 15 = 5.

Если, для удобства обозначения, перенумеровать яйца, то у нас будут

крутое № 1 …………… к1

крутое № 2 …………… к2

всмятку № 1 …………… с1

всмятку № 2 …………… с2

Из этих яиц можно составить следующие 10 пар:

к1 к2

к1 с1

к1 с2

к1 с3

к2 с1

к2 с2

к2 с3

с1 с2

с1 с3

Мы видим, что только одна пара – именно первая – состоит из крутых яиц, остальные 9 не дают требуемого сочетания. Значит, у вас только 1 шанс из 10 взять пару крутых яиц; в остальных 9-ти случаях из 10-ти вы проигрываете. И если вы ставите 1 рубль, то ваш партнер, имеющий 9 шансов выиграть, должен, для уравнения шансов, поставить не 5, а 9 рублей. Решение задачи № 87

При 4-х метаниях число всех возможных положений игральной кости равно 6x6x6x6 = 1296. Допустим, что первое метание уже состоялось, причем выпало единичное очко. Тогда при трех следующих метаниях число всех возможных положений, благоприятных для Петра (т. е. выпадений любых очков, кроме единичного) = 5x5x5 = 125. Точно также возможно по 125 благоприятных для Петра расположений, если единичное очко выпадет только при втором, только при третьем или только при четвертом метании. Итак, существует 125+125+125+125 = 500 различных возможностей для того, чтобы единичное очко при 4-х метаниях появилось один и только один раз. Неблагоприятных же возможностей существует 1296-500 = 796 (так как неблагоприятны все остальные случаи).

Мы видим, что у Владимира шансов выиграть больше (796 против 500), чем у Петра.

Нетрудно сообразить, что все семь друзей могли встречаться только через такое число дней, которое делится и на 2, и на 3, и на 4, и на 5, и на 6, и на 7. Наименьшее из таких чисел есть 420.

Следовательно друзья сходились все вместе только один раз в 420 дней (14 месяцев).

Каждый из восьми присутствующих (хозяин и 7 друзей) чокается с 7 остальными; всего, значит, сочетаний по два насчитывается 8x8 = 56. Но при этом каждая пара считалась дважды (например, 3-й гость с 5-м и 5-й с 3-м считались за разные пары). Следовательно, стаканы звучали

56/2 = 28 раз.