ЗАДАЧА № 51

Стакан гороху

Вы много раз держали в руках горошину и не менее часто имели дело со стаканом. Размеры того и другого вам должны быть поэтому хорошо знакомы. Представьте же себе теперь стакан, доверху наполненный горохом, и вообразите, что все эти горошины выставлены в один ряд, вплотную одна к другой.

Как вы думаете – был бы этот ряд длиннее обеденного стола или короче?

ЗАДАЧА № 52

Листья дерева

Если бы сорвать с какого-нибудь старого дерева – например с липы – все листья и положить их рядом, без промежутков, то какой приблизительно длины был бы этот ряд? Можно ли было бы, например, окружить им большой дом?

ЗАДАЧА № 53

Миллион шагов

Вы, конечно, очень хорошо знаете, что такое миллион, и столь же хорошо представляете себе длину своего шага. А раз вы знаете то и другое, то вам нетрудно будет ответить на вопрос: как далеко отошли бы вы, сделав миллион шагов? Больше, чем на 10 километров, или меньше?

ЗАДАЧА № 54

Квадратный метр

Я знал школьника, который, услышав впервые, что в квадратном метре миллион квадратных миллиметров, не хотел этому верить. Никакие разъяснения не были для него убедительны. «Откуда их берется так много? – недоумевал он. – Вот у меня лист миллиметровой бумаги, длиною и шириною ровно в метр. Неужели же в этом квадрате целый миллион миллиметровых клеточек? Ни за что не поверю».

– А ты пересчитай, – посоветовали ему.

– И пересчитаю! В воскресенье будет у меня свободное время, я и займусь этим делом.

В воскресенье он встал рано утром и сразу же принялся за счет, аккуратно отмечая точками сосчитанные квадратики. Каждую секунду появлялась новая точка под острием его карандаша; работал он усердно, и дело шло быстро.

Но убедился ли он в этот день, что квадратный метр заключает действительно миллион миллиметровых клеточек?

ЗАДАЧА № 55

Кубический метр

В одной школе учитель задал вопрос: какой высоты получился бы столб, если бы поставить один на другой все миллиметровые кубики, заключающиеся в кубическом метре?

– Это было бы выше Эйфелевой башни (300 метров)! – воскликнул один школьник.

– Даже выше Монблана (5 км), – ответил другой.

Кто из них ошибался больше?

ЗАДАЧА № 56

Кубический километр

Вообразите кубический ящик высотой в целый километр (немного менее версты). Как вы думаете, сколько таких ящиков понадобилось бы, чтобы вместить тела всех людей, живущих на свете? Примите во внимание, что население земного шара равно 1800 миллионам человек и что в одном кубическом метре можно уместить, средним счетом, 5 человеческих тел.

ЗАДАЧА № 57

Волос

Человеческий волос очень тонок: толщина его – около 20-й доли миллиметра. Но если бы волос был в миллион раз толще, какой примерно ширины был бы он? Один из моих знакомых, которому я задал этот вопрос, ответил, что волос был бы тогда толще круглой комнатной печи; другой утверждал, что волос был бы шириной во всю комнату. Оба, конечно, ошибались, – но кто ошибся больше?

ЗАДАЧА № 58

Сколько портретов?

Нарисуйте портрет на папке и разрежьте его на полосы, как показано на нашем рисунке, – положим, на 9 полос. Если вы умеете хоть немного рисовать, вам нетрудно будет изготовить еще такие же полосы с изображением различных частей лица, – однако так, чтобы каждые две соседние полосы, даже принадлежащие к разным портретам, можно было прикладывать одну к другой без нарушения непрерывности линий. Если вы для каждой части лица приготовите, например, 4 полосы, у вас будет 28 полос, из которых, складывая по 9, вы сможете составлять разнообразные портреты.

Рис. 42. Составные портреты.

В магазинах, где одно время продавали готовые наборы таких полос (или брусков) для составления портретов, продавцы уверяли покупателей, что из 36 полос можно получить т ы с я ч у различных физиономий.

Верно ли это?

Хотя французский замок известен всем, но устройство его знают лишь немногие. Поэтому часто приходится слышать сомнения в том, чтобы могло существовать большое число различных французских замков и ключей к ним. Достаточно, однако, познакомиться с остроумным механизмом этих замков, чтобы убедиться в возможности разнообразить их в достаточной степени.

Рис. 43-й изображает французский замок, как мы его видим с лица (кстати, – название «французский» совершенно неправильно, так как родина этих замков Америка, а изобретатель их американец Иэль, – почему на всех таких замках и ключах имеется надпись «Yale»). Вы видите вокруг замочной скважины небольшой кружок: это основание валика, проходящего через весь замок. Задача открывания замка заключается в том, чтобы повернуть этот валик, – но в этом-то и вся трудность. Дело в том, что валик удерживается в определенном положении пятью короткими стальными стерженьками (черт. 44). Каждый стерженек в каком-нибудь месте распилен надвое, и только если разместить стерженьки так, чтобы все разрезы приходились на уровне валика, можно будет его повернуть.

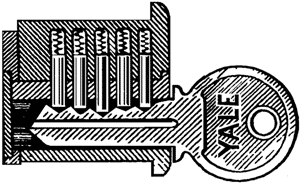
Рис. 44. Продольный разрез через французский замок.

Это необходимое расположение придает стерженькам ключ с соответственными выступами на краю: достаточно его вставить, чтобы стерженьки заняли то определенное и единственное расположение, которое необходимо для открытия замка.

Теперь легко понять, что число различных замков этого типа может быть действительно весьма велико. Оно зависит от того, сколькими способами можно разрезать каждый стержень на две части; число это, разумеется, не бесконечно, если принять во внимание ограниченную высоту зубчиков ключа.

Предположите, что каждый стерженек можно разрезать на две части 10-ю способами, и попробуйте сосчитать, сколько же различных французских замков можно при таком условии изготовить?

Задача, которую я вам сейчас предложу, не нова, даже очень не нова. Она общеизвестна, но именно потому я и включил ее в этот сборник головоломок. Ведь книжка моя предназначается не для тех, кто знает все общеизвестное, а для тех, кому это еще должно стать известным.

Итак, пусть вам станет отныне известна старинная легенда о том, какую награду попросил себе древний мудрец Сета у индусского правителя Шерама за то, что придумал шахматную игру. Мудрец просил вознаградить его за изобретение шахматной доски тем, чтобы выдать за первое ее поле всего 1 пшеничное зерно, за второе поле – 2 зерна, за третье – 4, за четвертое – 8 и т. д., удваивая вознаграждение за каждое следующее поле, пока не будут оплачены все 64 поля доски. Что же касается шахматных фигур, то за них мудрец никакой награды не требовал.

Правитель подивился такой скромности и отпустил мудреца, приказав немедленно выдать ему следуемые зерна.

Когда спустя некоторое время правитель осведомился, исполнено ли в точности его приказание, ему в смущении ответили, что требуемая награда не может быть выдана.

– Почему? – спросил правитель.

– Почему? – спросим и мы читателя.

РЕШЕНИЯ ЗАДАЧ №№ 51-60

Ряд горошин был бы гораздо длиннее стола. Поперечник горошины равен, примерно, от 1/2 до 1/3 сантиметра. Если остановимся на последнем размере, то в кубике с ребром в 1 сантиметр должно умещаться не менее 2x2x2 = 8 горошин; следовательно, в стакане емкостью 200 куб. сантиметров число горошин должно быть не меньше 1600. Расположив их в один ряд, получим длину 1/2 x 1600 = 800 сантиметров, или 8 метров. Это составляет 4 сажени – расстояние гораздо длиннее любого стола.

Если исходить из размера горошины 1/3 сантиметра, то в куб. сантиметре помещается их не менее 3x3x3 = 27, а в стакане – не менее 27x200 = 5400. Длина ряда из 5400 таких горошин равна 1/3 x 5400 = 1800 сантиметров, или 18 метров – еще больше, чем в случае крупных горошин.

Не только дом, но и иной губернский город можно было бы окружить расположенными в ряд листьями одного дерева, потому что такой ряд тянулся бы верст на десять! В самом деле: на старом дереве не менее 200–300 тысяч листьев. Если остановиться даже на числе 250000 и считать каждый лист шириною в 5 сантиметров, то ряд получается длиною в 1250000 сантиметров, т. е. 12500 метров, или 12 1/2 километров.

Миллион шагов гораздо больше 10 километров, больше даже 100 километров. Если длина шага примерно 3/4 метра, то 1000000 шагов = 750 километров. Так как от Москвы до Ленинграда всего 640 километров, то, сделав от Москвы миллион шагов, вы отошли бы дальше, чем на расстояние до Ленинграда.

В тот же день школьник в этом убедиться не мог, потому что, если бы он даже работал круглые сутки без перерыва, он не пересчитал бы и десятой доли всех клеточек. Действительно, в сутках 24x60x60 = 86400 секунд, а в квадратном метре 1000000 квадр. миллиметров. Понадобилось бы более 11 суток непрерывной работы, чтобы проверить прямым счетом, действительно ли в квадратном метре миллион миллиметровых клеточек. Если же считать по десять часов в сутки, то на подобную проверку понадобилось бы около месяца. Мало у кого достанет терпения выполнить такой счетный подвиг [15] .

Оба ответа далеки от истины, потому что столб получился бы во сто раз выше самой высокой горы на земле. Действительно: в кубическом метре 1000x1000x1000, т. е. миллиард кубических миллиметров. Поставленные один на другой, они образовали бы столб высотою в 1000000000 миллиметров, или 1000000 метров, или 1000 километров!

В одном ящике указанных размеров не только поместятся все люди земного шара, но могло бы поместиться почти втрое больше! Легко вычислить, что если 5 человек занимают объем в 1 куб. метр, то 1800000000 человек заняли бы 360 миллионов кубических метров, – между тем в кубическом километре 1000 миллионов кубических метров.

Волос, если бы был в миллион раз толще, превосходил бы по ширине не только любую печку или комнату, но и почти любое здание, потому что поперечник его равнялся бы 50 метрам!

Действительно, умножим ширину волоса 0,05 мм на 1000000. Получим 50000 мм, или 50 метров.

Такую ширину имела бы, между прочим, и каждая точка типографского шрифта этой книги, если бы она увеличилась в поперечнике в миллион раз. А каждая буква имела бы при подобном увеличении более двух верст в высоту!

Эти неожиданные результаты показывают, что представление наше о миллионе далеко не так отчетливо, как мы обычно думаем.

Число портретов значительно больше тысячи. Сосчитать их можно следующим образом. Обозначим девять частей портретов римскими цифрами I, II, III, IV, V, VI, VII, VIII и IX; для каждой части имеются 4 полоски, которые мы перенумеруем арабскими цифрами 1, 2, 3, 4.

Возьмем полоску I, 1. Мы можем присоединить к ней полоски II, 1; II, 2; II, 3; II, 4.

Всего, следовательно, здесь возможны 4 сочетания. Но так как часть головы I может быть представлена четырьмя полосками (I, 1; I, 2; I, 3; I, 4) и каждая из них может быть соединена с частью II четырьмя различными способами, то две верхние части головы I и II могут быть соединены 4x4 = 16 различными способами.

К каждому из этих 16 расположений можно присоединить часть III четырьмя способами (III, 1; III, 2; III, 3; III, 4), следовательно, первые три части физиономии могут быть составлены 16x4 = 64 различными способами.

Таким же образом узнаем, что части I, II, III, IV могут быть расположены 64x4 = 256 различными способами; части I, II, III, IV, V – 1024 способами; части I, II, III, IV, V, VI – 4096 способами и т. д.; наконец, все девять частей портрета можно соединить 4x4x4x4x4x4x4x4x4, т. е. 262144 способами.

Итак, из 9 наших брусков возможно составить не 1000, а больше четверти миллиона различных портретов!

Задача весьма поучительна: она объясняет нам, почему так редко встречаются две одинаковые человеческие физиономии. Еще Владимир Мономах в своем «Поучении» изумлялся тому, что при огромном числе людей на свете каждый имеет свое особое лицо. Но мы сейчас убедились, что если бы человеческое лицо характеризовалось всего 9-ю чертами, допускающими каждая всего 4 видоизменения, то могло бы существовать более 260000 различных лиц. В действительности же характерных черт человеческого лица гораздо больше 9, и видоизменяться они могут больше чем 4 способами. Так, при 20 чертах, варьирующих каждая на 10 ладов, мы имеем различных лиц:

10x10x10x10… (20 множителей), т. е.

100000000000000000000.

Это во много раз больше, чем людей во всем мире (1800000000).

Рассуждая подобно тому, как и при решении предыдущей задачи, нетрудно сосчитать, что число различных замков равно 10x10x10x10x10 = 100000.

Каждому из этих 100000 замков соответствует особый ключ, – единственный, которым возможно его открыть. Существование ста тысяч различных замков и ключей, конечно, вполне обеспечивает владельца замка, так как у желающего вкрасться в помещение с помощью подобранного ключа есть только 1 шанс из 100000 напасть на подходящий ключ.

Наш подсчет только примерный: он сделан в предположении, что каждый стерженек замка может быть разделен надвое только 10-ю способами. В действительности это возможно сделать, вероятно, большим числом способов, и тогда число различных замков значительно увеличивается.

«Скромная награда» не могла быть выдана потому, что не только в Индии, но и во всем мире нет того количества зерен, какое она насчитывает!

Самое вычисление затребованной суммы зерен представляет собой нелегкую задачу. В самом деле: требуется сложить ряд чисел:

1+2+4+8+16+32+64+128+ и т. д.

Здесь выписаны только первые 8 чисел. Но остается еще 56. Чтобы узнать последнее, 64-е число, нужно умножить число 2 само на себя 62 раза. Индусы, – они не знали еще логарифмов, сокращающих подобные вычисления, – должны были выполнить это умножение обычными приемами арифметики; а стоит лишь приступить к этой работе, чтобы ощутить, насколько это утомительно. Правда, можно облегчить себе работу и сэкономить много времени, разбив наши 63 множителя на группы, по 7 двоек в каждом; тогда придется перемножить «только» 9 множителей, каждый из которых равен 128, – или же, если хотите, «всего» три множителя, каждый из которых = (128x128x128). Но на деле вы убедились бы, что слова «только» и «всего» недаром взяты здесь в кавычки, потому что работы остается предостаточно. А ведь это только одно последнее, 64-е слагаемое; надо же знать все предыдущие 63 слагаемых, да кроме того эти числа сложить…

Для тех, кто проходил алгебру и знаком с логарифмами и прогрессиями, выполнение этого расчета – правда, лишь приближенное, с точностью до 100000-й доли результата – не составило бы никакого труда. Так как у читателей этой книжки я не могу предполагать таких познаний из алгебры, а с другой стороны, не собираюсь засадить их за многочасовые выкладки, то укажу простой способ получить хотя бы грубо-приблизительное представление об истинных размерах «скромной награды» индусского мудреца.

Продолжив ряд

2, 4, 8, 16, 32, 64 и т. д.

до 10-го члена его, мы получим 1024. Так как мы стремимся только приблизительно определить, как велико последнее слагаемое, то позволительно в числе 1024 откинуть 24 единицы, чтобы получить круглое число 1000. Если первые десять двоек при перемножении дали около 1000, то столько же получится от умножения и следующих 10 двоек, а также дальнейших групп из 10 двоек. Всех множителей-двоек у нас 63, т. е. шесть групп по 10 и еще седьмая группа из трех двоек. Значит, число зерен, причитающееся изобретателю за последнее, 64-е поле шахматной доски должно приблизительно равняться

1000x1000x1000x1000x1000x1000x(2x2x2) = 8000000000000000000.

Восемь триллионов зерен – вот примерная величина последнего слагаемого!

Чтобы вычислить (приблизительно) всю сумму, обратим внимание на поучительную особенность ряда

1, 2, 4, 8, 16, 32, 64, 128 и т. д.

Легко заметить, что каждое число в нем равно сумме всех предыдущих, увеличенной на 1. Например:

8 = (1+2+4)+1; 16 = (1+2+4+8)+1; 32 = (1+2+4+8+16)+1.

Понятно, что и последнее, 64-е число этого ряда равно сумме 63-х предыдущих + 1. Но мы уже знаем, что это последнее число равно (приблизительно) 8-ми триллионам. Следовательно, сумма всех предыдущих чисел тоже приблизительно равна 8 триллионам, а общее число всех зерен, причитающихся изобретателю, приблизительно равно

16000000000000000000.

Результат этот, однако, заведомо меньше истинного – вспомните, что в каждом из 6 множителей мы откидывали 24 единицы (брали ровно 1000 вместо 1024). Точное вычисление дало бы результат:

18446744073709551515.

Чтобы помочь вам ощутить огромность этого числа, замечу, что в кубическом метре (80-ведерной бочке) помещается 15 миллионов пшеничных зерен. «Скромная награда» должна была поэтому занять объем приблизительно в 12000000000000 кубических метров. Это составляет 12000 кубических километров!

Далее. Поверхность земного шара – всех его материков и океанов – равна 500 биллионам кв. метров. Значит, если рассыпать наше число зерен ровным слоем по всему миру, то слой этот имел бы в толщину 12:500 = 0,024 метра, или примерно 1/4 сантиметра. Будь земной шар целиком превращен в сплошное пшеничное поле (для чего понадобилось бы осушить океаны, растопить полярные льды и оросить все пустыни), то урожай целиком пошел бы в награду изобретателю шахматной игры.