ЗАДАЧИ №№ 61-70 – Чем эта муха на кристалле вас так заинтересовала? – Своим
странным поведением: она ходит по кристаллу, право, не без системы.
Посмотрите, все время придерживается она ребер и не ступает по граням.
Что за охота ей ходить по гребням, когда рядом сколько угодно плоских
мест? – Мне кажется, дело довольно просто. Чем склеены у вас грани этого кристалла? – Вы
подозреваете, что в клее есть что-то сладкое, привлекающее муху?
Кажется, вы правы; она действительно вылизывает хоботком ребра
кристалла. Так вот почему она медленно и систематически переходит с
одного ребра на другое! – И при этом на практике разрешает интересную задачу: обойти весь многогранник по его ребрам, не посещая дважды ни одного ребра. – Разве это возможно? – В данном случае вполне: ведь этот кристалл – восьмигранник. – Да, октаэдр. Что же из этого? – У него на каждой вершине сходятся 4 ребра. – Разумеется. Но какое же отношение имеет это к нашей задаче? – Самое
непосредственное. Задача обойти все ребра многогранника, и притом не
более чем по одному разу, разрешима только для тех многогранников, у
которых на каждой вершине сходится четное число ребер. 
Рис. 45. Муха на кристалле. – Вот как! Я об этом не знал. Почему же? – Почему
у каждой вершины должно сходиться именно четное число ребер? Очень
просто. Надо ведь на каждую вершину попасть и надо с нее уйти, – значит,
нужно, чтобы к ней вела одна дорога и от нее отходила другая, т. е.
чтобы у нее сходилась пара ребер. Если же, продолжая путешествовать по
кристаллу, вы попадете на ту же вершину вторично, т. е. если к ней ведет
еще и третье ребро, то должно иметься непременно и четвертое ребро,
чтобы вы могли уйти с этой вершины, а не очутиться в тупике. Другими
словами, число ребер, сходящихся у каждой вершины, должно быть парное,
т. е. четное. Если хотя бы одна вершина многогранника имеет нечетное
число сходящихся к ней ребер, то на такую вершину вы, исчерпав все
ведущие к ней парные ребра, можете попасть, конечно, по последнему
неиспользованному ребру, – но покинуть этой вершины уже не сможете:
путешествие здесь поневоле оборвется. – Но я могу ведь совсем не воспользоваться этим ребром, раз оно заведомо ведет в тупик! – Тогда вы не выполните другого условия нашего путешествия: пройти по всем ребрам без исключения. – Позвольте:
но может же случиться, что это ребро как раз последнее и единственное
еще не пройденное. Тогда нет вовсе надобности покидать его: оно и будет
конечной целью путешествия. – Совершенно
правильно. И если бы в фигуре была только одна «нечетная» вершина, то
вам нужно было бы избрать такой маршрут, чтобы вершина эта оказалась
последним этапом, – тогда вы разрешили бы задачу успешно. Или же можете
начать с этой вершины – тогда вам не придется на нее возвращаться. Я
должен только прибавить к этому, что фигуры с одной «нечетной» вершиной
существовать не может: таких вершин должно быть четное число – две,
четыре, шесть и т. д. – Это почему же? – Подумайте
о том, что каждое ребро соединяет две вершины. И если какая-нибудь
вершина имеет ребро без пары, то ребро это должно упираться в
какую-нибудь соседнюю вершину и там тоже быть непарным ребром. – А
если соседняя вершина была бы без этого ребра тоже нечетная? Тогда
новое ребро делает ее «четной», и наша «нечетная» вершина остается
одинокой. – Этого не может быть. Если
без нашего ребра у соседней вершины сходится нечетное число ребер, то,
значит, одно из ее ребер, остающееся вне пары, соединено со следующей
вершиной, и следовательно «нечетная» вершина будет найдена дальше, но
все же будет существовать. Вы видите, что если в фигуре имеется одна
«нечетная» вершина, то непременно должна существовать и вторая. Число
«нечетны х» вершин не может быть нечетным. Поясню это еще и иным путем,
пожалуй, более простым. Предположите, что вы желаете сосчитать, сколько
ребер в какой-нибудь фигуре. Вы считаете ребра, сходящиеся у одной
вершины, прибавляете ребра, сходящиеся у второй, потом – у третьей и
т. д. Когда вы все это сложите, что у вас получится? – Двойное число ребер фигуры, потому что каждое ребро считалось по два раза: ведь каждое ребро соединяет две вершины. – Именно.
Вы получите удвоенное число ребер. И если допустить, что у одной из
вершин сходится нечетное число ребер, а у всех прочих – четное, то
результат сложения будет, конечно, число нечетное. Но может ли удвоен –
ное целое число быть нечетным? – Не
может, конечно. Теперь мне вполне ясно, что «нечетных» вершин во всякой
фигуре должно быть две, четыре – вообще, четное число. Все же я думаю,
что и кристалл с двумя «нечетными» вершинами возможно обойти. Пусть у
нас имеется фигура с двумя «нечетными» вершинами. Что мешает начать
путешествие именно в одной из этих точек и закончить в другой? Тогда не
понадобится ни возвращаться в первую, ни уходить из последней.
Путешествие будет выполнено с соблюдением всех требуемых условий. – Правильно!
В этом и состоит секрет успешного выполнения подобных путешествий, или –
что то же самое – правило вычерчивания фигур одним почерком пера. Если
требуется непрерывным движением начертить фигуру – безразлично, в
плоскости или в пространстве, – то прежде всего внимательно рассмотрите
фигуру и определите, имеются ли у нее «нечетные» вершины, т. е. такие
вершины, у которых встречается непарное число линий. Если подобных
вершин в фигуре больше двух, то задача неразрешима. Если только две, –
то нужно начать вычерчивание из одной «нечетной» точки и закончить в
другой. Если «нечетных» вершин вовсе нет, то можете начинать чертить из
любой вершины, и всегда найдется способ выполнить всю фигуру,
возвратившись к начальной точке. Каким путем вы в таком случае поведете
перо – безразлично. Надо только заботиться о том, чтобы не вести линию к
вершине, от которой нет больше пути, т. е. стараться не замыкать фигуры
раньше времени. Вот пример: фигура в форме буквы Ф (черт. 46). Можно ли
ее начертить одним почерком пера? 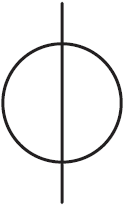
Рис. 46. – В ней всего две «нечетные» вершины, именно концы палки. Значит, ее начертить одним почерком пера возможно. Но как? – Надо начать с одного конца палки и кончить другим, вот так (черт. 47). 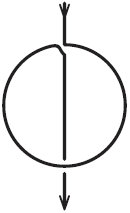
Рис. 47. – В
детстве я ломал свою голову над тем, чтобы начертить одним почерком
пера четырехугольник с двумя диагоналями (черт. 48). Мне этого никак не
удавалось сделать. 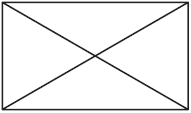
Рис. 48. – И
не удивительно: ведь в ней 4 нечетных вершины – углы четырехугольника.
Бесполезно даже ломать голову над этой задачей: она неразрешима. – А такая фигура (черт. 49)? 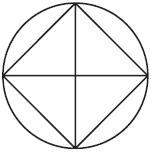
Рис. 49. – Ее
тоже нельзя начертить одной непрерывной линией, потому что у нее 4
вершины, в каждой из которых сходится по 5 линий, т. е. у нее 4
«нечетных» вершины. Зато легко
начертить фигуры черт. 50-й и 51-й: у них все вершины «четные» (решение
для черт. 51 – см. чер. 52). Теперь перейдем к той задаче, которую
собирается решить наша муха: обойти по одному разу все ребра октаэдра
непрерывным движением. На каждой вершине этой фигуры сходятся 4 ребра;
в ней вовсе нет «нечетных» вершин. Поэтому вы можете начать
путешествовать с любой вершины и возвратитесь в исходную точку. Вот одно
из возможных решений (черт. 53): 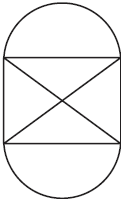
Рис. 50. 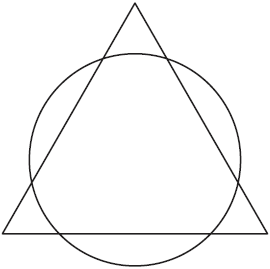 Рис. 51. Рис. 51.
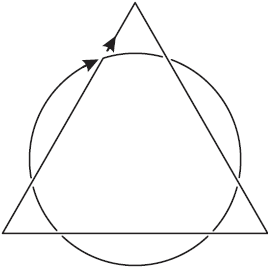 Рис. 52. Рис. 52.
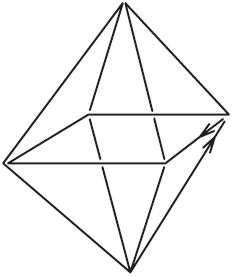 Рис. 53. Рис. 53.
– А знаете, это интересный род головоломок! Дайте мне десяток подобных задач, я подумаю о них на досуге. – Извольте. РЕШЕНИЯ ЗАДАЧ №№ 61–70. Из
представленных на стр. 210 и 211 фигур безусловно могут быть начерчены
непрерывной линией фигуры 62-я, 64-я, 65-я, 67-я, 68-я, 69-я и 70-я. В
этих фигурах у всех точек пересечения сходится четное число линий, –
следовательно, можно начать чертить с любой точки. Каждая точка может
служить начальной, она же будет и конечной. Выполнение чертежей показано
на стр. 212 и 213. Фигура 61-я
заключает только две «нечетные» точки, именно те места, где ручка
молотка входит в головку: у них сходится по 3 линии. Поэтому фигуру
можно начертить непрерывной линией только в том случае, если начать в
одной из «нечетных» точек и кончить в другой. То
же относится и к фигуре 63-й: она содержит только две «нечетных» точки,
m и n: они и должны быть начальной и конечной точкой при черчении. Фигура 66-я заключает более двух «нечетных» точек, – а потому ее совершенно невозможно начертить одной непрерывной линией. 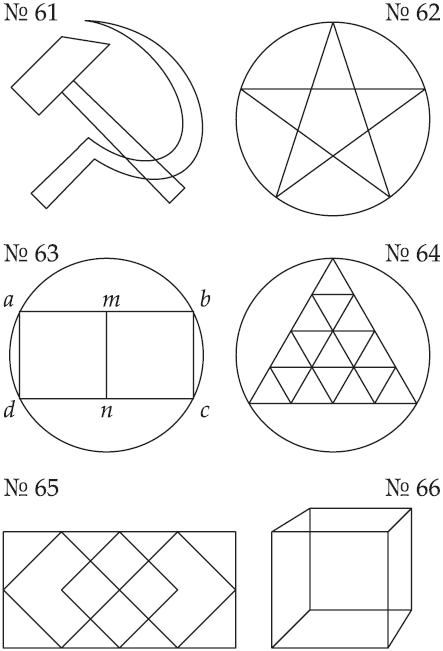
Рис. 54. Задачи на непрерывное вычерчивание фигур: №№ 61–66. 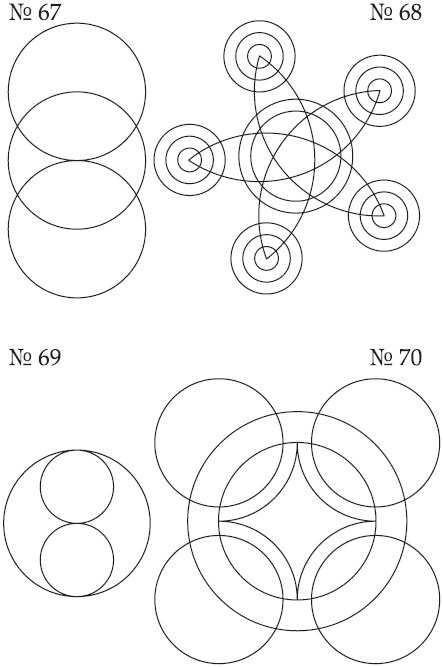
Рис. 55. Задачи на непрерывное вычерчивание фигур: №№ 67–70. 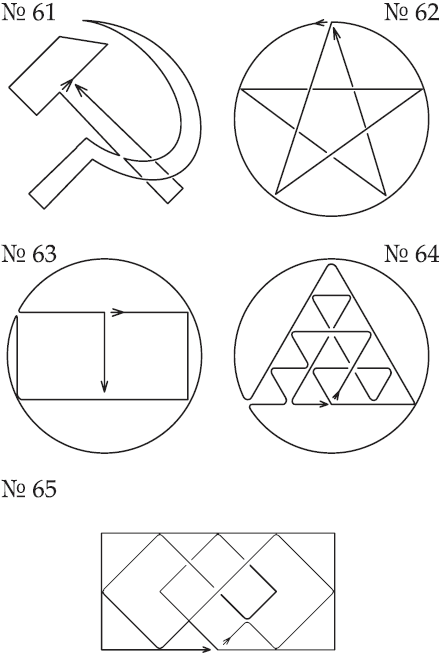
Рис. 56. Решение задач: №№ 61–65. 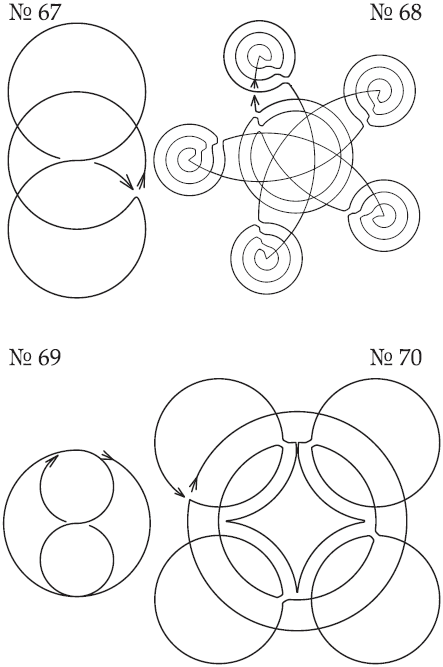
Рис. 57. Решение задач: №№ 67–70.
| 
