ЗАДАЧА № 21 Вес бревна Круглое бревно весит тридцать килограммов. Сколько весило бы оно, если бы было втрое толще, но вдвое короче? ЗАДАЧА № 22 Десятичные весы Сто
килограммов железных гвоздей уравновешены на десятичных весах железными
гирями. Весы затопило водой. Сохранили ли они равновесие и под водой? ЗАДАЧА № 23 Вес бутылки Бутылка,
наполненная керосином, весит 1000 граммов. Та же бутылка, наполненная
кислотой, весит 1600 граммов. Кислота вдвое тяжелее керосина. Сколько весит бутылка? ЗАДАЧА № 24 Брусок мыла На одной чашке весов положен брусок мыла, на другой 3/4 такого же бруска и еще 3/4 килограмма. Весы в равновесии. 
Рис. 20. Сколько весит брусок мыла? Сколько весит целый брусок мыла? Постарайтесь решить эту несложную задачу устно, без карандаша и бумаги. ЗАДАЧА № 25
Кошки и котята Из прилагаемого рисунка 21-го вы усматриваете, что 4 кошки и 3 котенка весят 15 килограммов, а 3 кошки и 4 котенка весят 13 килограммов. 
Рис. 21. Сколько весят кошка и котенок порознь? Сколько же весит каждая кошка и каждый котенок в отдельности? Постарайтесь и эту задачу решить устно. ЗАДАЧА № 26
Раковина и бусины Рисунок
22-й показывает вам, что 3 детских кубика и 1 раковина уравновешиваются
12-ю бусинами, и что, далее, 1 раковина уравновешивается 1 кубиком и
8-ю бусинами. Сколько же бусин нужно положить на свободную чашку весов, чтобы уравновесить раковину на другой чашке? 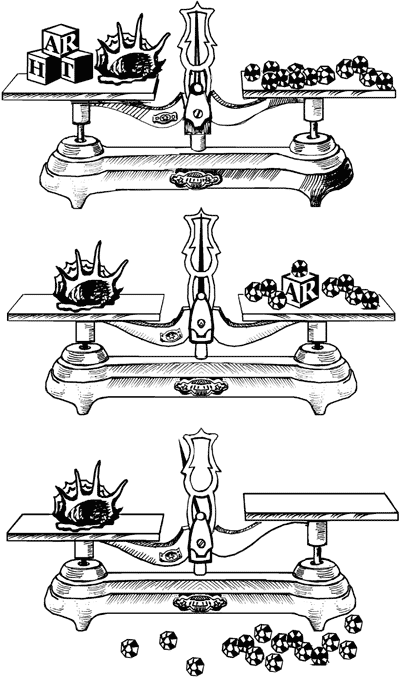
Рис. 22. Задача о раковине и бусинах. ЗАДАЧА № 27
Вес фруктов Вот еще задача в том же роде. Рисунок 23-й показывает, что 3 яблочка и 1 груша весят столько, сколько 10 персиков, а 6 персиков и 1 яблочко весят столько, сколько 1 груша. Сколько же персиков надо взять, чтобы уравновесить одну грушу? 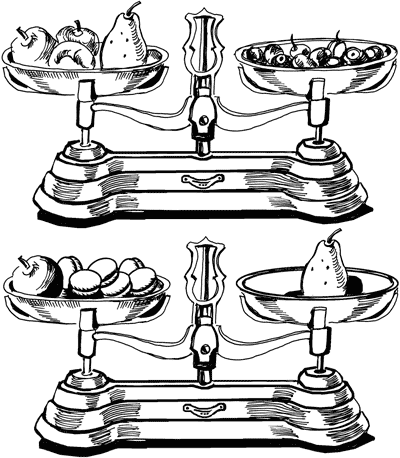
Рис. 23. Задача о груше и персиках. ЗАДАЧА № 28
Сколько стаканов? На
рисунках 24-а и 24-б вы видите, что бутылка и стакан уравновешиваются
кувшином; бутылка сама по себе уравновешивается стаканом и блюдцем; два
кувшина уравновешиваются тремя блюдцами. 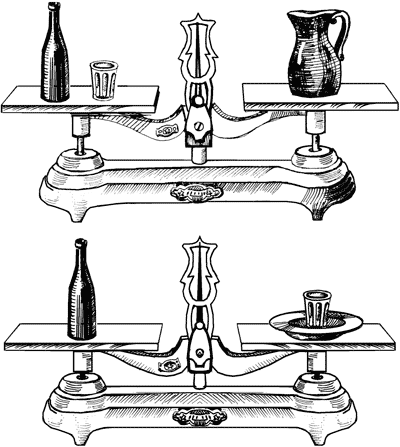
Рис. 24-а. Задача о стаканах и бутылке. 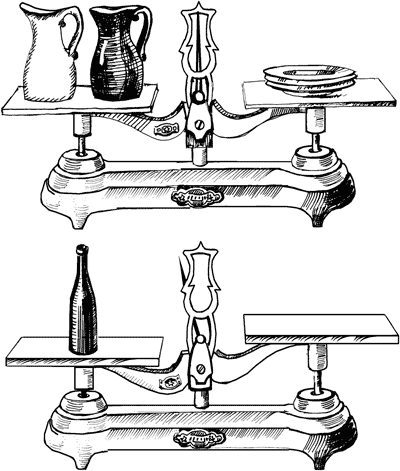
Рис. 24-б. Чем уравновесить бутылку? Сколько надо поставить стаканов на свободную чашку весов, чтобы уравновесить бутылку? ЗАДАЧА № 29
Гирей и молотком Надо
развесить 2 килограмма сахарного песку на 200 граммовые пакеты. Имеется
только одна 500-граммовая гиря, да еще молоток, весящий 900 граммов. 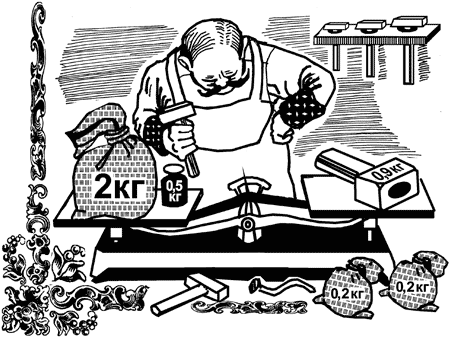
Рис. 25. Затруднение при развешивании. Как получить все 10 пакетов, пользуясь этой гирей и молотком?
ЗАДАЧА № 30
Задача Архимеда Самая
древняя из головоломок, относящихся к взвешиванию – без сомнения, та,
которую древний правитель сиракузский Гиерон задал знаменитому
математику Архимеду. Предание
повествует, что Гиерон поручил мастеру изготовить венец для одной статуи
и приказал выдать ему необходимое количество золота и серебра. Когда
венец был доставлен, взвешивание показало, что он весит столько же,
сколько весили вместе выданные золото и серебро. Однако правителю
донесли, что мастер утаил часть золота, заменив его серебром. Гиерон
призвал Архимеда и предложил ему определить, сколько золота и сколько
серебра заключает изготовленная мастером корона. Архимед решил эту
задачу, исходя из того, что чистое золото теряет в воде 20-ю долю своего
веса, а серебро – 10-ю долю. Если вы
желаете попытать свои силы на подобной задаче, примите, что мастеру было
отпущено 8 килограммов золота и 2 кг серебра, и что, когда Архимед
взвесил корону под водой, она весила не 10 кг, а всего 9 1/4 кг.
Попробуйте определить по этим данным, сколько золота утаил мастер. Венец
предполагается изготовленным из сплошного металла, без пустот. РЕШЕНИЯ ЗАДАЧ О ВЕСАХ И ВЗВЕШИВАНИИ (№№ 21–30) Решение задачи № 21 Обыкновенно
отвечают, что бревно, увеличенное в толщину вдвое, но вдвое же
укороченное, не должно изменить своего веса Однако это не верно. От
увеличения поперечника вдвое объем круглого бревна увеличивается
вчетверо; от укорочения же вдвое объем уменьшается всего в два раза.
Поэтому толстое короткое бревно должно быть вдвое тяжелее длинного
тонкого, т. е. весить 60 килограммов. Решение задачи № 22 При
погружении в воду железная вещь (сплошная) теряет 8-ю долю своего веса
[12] . Поэтому гири под водой будут иметь 7/8 прежнего веса, гвозди –
также 7/8 своего прежнего веса. И так как гири были в 10 раз легче
гвоздей, то и под водой они легче их в 10 раз. Следовательно, десятичные
весы останутся и под водой в равновесии. Решение задачи № 23 Из условия задачи мы знаем, что, во-первых, вес бутылки + вес керосина = 1000 граммов. А во-вторых, так как кислота вдвое тяжелее керосина, мы знаем, что вес бутылки + двойной вес керосина = 1600 граммов. Отсюда
ясно, что разница в весе 1600–1000, т. е. 600 граммов, есть вес
керосина в объеме бутылки. Но бутылка вместе с керосином весит
1000граммов; значит, бутылка весит 1000-600 = 400 граммов. Действительно: вес кислоты (1600-400 = 1200 гр.) оказывается вдвое больше веса керосина. Решение задачи № 24 3/4
бруска мыла + 3/4 килограмма весят столько, сколько целый брусок. Но в
целом бруске содержится 3/4 бруска + 1/4 бруска. Значит, 1/4 бруска
весит 3/4 килограмма. И следовательно, целый брусок весит в четыре раза
больше, чем 3/4 кг, т. е. 3 килограмма. Решение задачи № 25 Сравнивая
оба взвешивания, легко видеть, что от замены одной кошки одним котенком
вес груза уменьшился на 15–13, т. е. на 2 кг. Отсюда следует, что кошка
тяжелее котенка на 2 кг. Зная это, заменим при первом взвешивании всех
четырех кошек котятами: у нас будет тогда всех 4+3 = 7 котят, а стрелка
весов вместо 15 килограммов покажет на 2x4, т. е. на 8 кг меньше.
Значит, 7 котят весят 15-8 = 7 килограммов. Отсюда ясно, что котенок весит 1 килограмм, взрослая же кошка 1+2 = 3 килограмма. Решение задачи № 26 Сравним
первое и второе взвешивание. Вы видите, что раковину при первом
взвешивании мы можем заменить 1 кубиком и 8 бусинами, потому что они
имеют одинаковый вес. У нас оказалось бы тогда на левой чашке 4 кубика и
8бусин, и это уравновешивалось бы 12 бусинами. Сняв теперь с каждой
чашки по 8 бусин, мы не нарушим равновесия, останется же у нас на левой
чашке 4 кубика, на правой – 4 бусины. Значит, кубик и бусина весят
одинаково. Теперь ясно, сколько бусин весит раковина: заменив (второе взвешивание) 1 кубик на правой чашке бусиной, узнаем, что вес раковины = весу 9 бусин. Результат
наш легко проверить: замените при первом взвешивании кубики и раковины
на левой чашке соответственным числом бусин: получите 3+9 = 12, как и
должно быть. Решение задачи № 27 Заменим
при первом взвешивании 1 грушу 6-ю персиками и яблочком: мы вправе это
сделать, так как груша весит столько же, сколько 6персиков и яблочко. У
нас окажется на левой чашке 4 яблочка и 6 персиков, на правой – 10
персиков. Сняв с обеих чашек по 6персиков, узнаем, что 4 яблочка весят
столько, сколько и 4 персика. Другими словами, один персик весит столько
же, сколько одно яблочко. Теперь легко уже сообразить, что вес груши
равен весу 7 персиков. Решение задачи № 28 Задачу эту можно решать на разные лады. Вот один из способов. Заменим
при третьем взвешивании каждый кувшин одной бутылкой и 1стаканом (из
первого взвешивания мы видим, что весы при этом должны оставаться в
равновесии). Мы узнаем тогда, что 2 бутылки и 2 стакана уравновешиваются
3 блюдцами. Каждую бутылку мы, на основании второго взвешивания, можем
заменить 1 стаканом и 1 блюдцем. Окажется тогда, что 4 стакана и 2 блюдца уравновешиваются 3 блюдцами. Сняв с каждой чашки весов по 2 блюдца, узнаем, что 4 стакана уравновешиваются 1 блюдцем. И следовательно, бутылка уравновешивается (ср. второе взвешивание) 5 стаканами. Решение задачи № 29 Порядок
отвешивания таков. Сначала кладут на одну чашку молоток, на другую гирю
и столько сахарного песку, чтобы чашки уравновесились; ясно, что
насыпанный на эту чашку песок весит 900–500 = 400 граммов. Ту же
операцию выполняют еще 3 раза; остаток песку весит 2000-(4x400) = 400
граммов. Теперь остается только каждый
из пяти полученных 400-граммовых пакетов разделить пополам, на два
равных по весу пакета. Делается это без гирь очень просто: рассыпают
содержимое 400-граммового пакета в два картуза, поставленные на разных
чашках, пока весы не уравновесятся. Решение задачи № 30 Если бы
заказанный венец был сделан целиком из чистого золота, он весил бы вне
воды 10 кг, а под водой потерял бы 20-ю долю этого веса, т. е.
полкилограмма. В действительности же венец, мы знаем, теряет в воде не
1/2 кг, а 10 – 9 1/4 = 3/4 кг. Это потому, что он содержит в себе
серебро, металл, теряющий в воде не 20-ю, а 10-ю долю своего веса.
Серебра должно быть в венце столько, чтобы венец терял в воде не 1/2 кг,
а 3/4 кг – на 1/4 кг более. Если в нашем чисто золотом венце заменим
мысленно 1 кг золота серебром, то венец будет терять в воде больше,
нежели прежде, на 1/10 – 1/20 = 1/20 кг. Следовательно, чтобы получилось
требуемое увеличение потери веса на 1/4 кг, необходимо заменить
серебром столько килограммов золота, сколько раз 1/20 кг содержится в
1/4 кг; но 1/4 : 1/20 = 5. Итак, в венце было 5 кг серебра и 5 кг
золота, – вместо выданных 2 кг серебра и 8 кг золота. Три килограмма
золота было утаено и заменено серебром.
| 
