ЗАДАЧА № 11 Из шести три Перед
вами (рис. 5) фигура, составленная из 17 спичек. Вы видите в ней 6
одинаковых квадратов. Задача состоит в том, чтобы убрать 5 спичек, не
перекладывая остальных, – и осталось бы всего 3 квадрата. 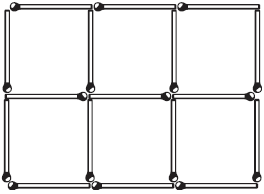
Рис. 5. ЗАДАЧА № 12
Оставить пять квадратов В
решетке из спичек, представленной на рис. 6-м, нужно так убрать 4
спички, – не трогая остальных, – чтобы осталось пять квадратов. 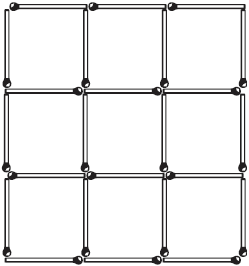
Рис. 6. ЗАДАЧА № 13 Оставить четыре квадрата Из той же фигуры (рис. 6) тáк выньте 8 спичек, – не трогая других, – чтобы оставшиеся спички составляли 4 одинаковых квадрата. ЗАДАЧА № 14
Оставить три квадрата В той же решетке (рис. 6) тáк уберите 6 спичек, – не перекладывая остальных, – чтобы осталось всего 3 квадрата. ЗАДАЧА № 15
Оставить два квадрата И наконец, в той же фигуре (рис. 6) тáк уберите 8 спичек, – не трогая остальных, – чтобы осталось всего лишь два квадрата. ЗАДАЧА № 16
Шесть четырехугольников В
фигуре, представленной на рис. 7, нужно тáк переложить 6 спичек с
одного места на другое, чтобы образовалась фигура, составленная из 6
одинаковых четырехугольников. 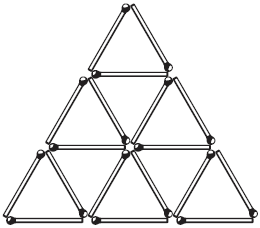
Рис. 7. ЗАДАЧА № 17
Из дюжины спичек Из 12 спичек нужно составить фигуру, в которой было бы: три одинаковых четырехугольника и два одинаковых треугольника. Как это сделать? ЗАДАЧА № 18
Из полутора дюжин Из
18 спичек нужно сложить два четырехугольника так, чтобы площадь одного
была втрое больше площади другого. Спичек, как и во всех предыдущих
задачах, переламывать нельзя. Оба четырехугольника должны лежать
обособленно, не примыкая друг к другу. ЗАДАЧА № 19
Два пятиугольника Если вам удалось решить предыдущую задачу, попытайте силы на такой головоломке: Из
18 спичек сложить два пятиугольника так, чтобы площадь одного была
ровно втрое больше площади другого. Прочие условия те же, что и в
предыдущей задаче. ЗАДАЧА № 20
Из 19 и из 12 На чертеже 8-м вы видите, как можно 19-ю целыми спичками ограничить шесть одинаковых участков. 
Рис. 8. А можно ли ограничить шесть одинаковых участков, хотя бы и иной формы – 12-ю целыми спичками? РЕШЕНИЯ ЗАДАЧ СО СПИЧКАМИ (№№ 11–20) Решение задачи № 11 видно из чертежа 9-го. 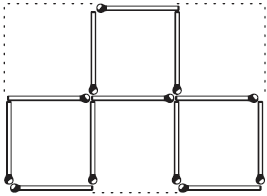
Рис. 9. Решения задач №№ 12, 13, 14 и 15 показаны на чертежах 10-м, 11-м, 12-м, 13-м, 14-м. 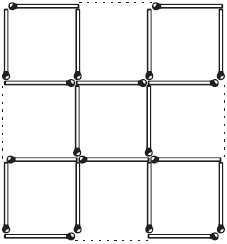
Рис. 10. 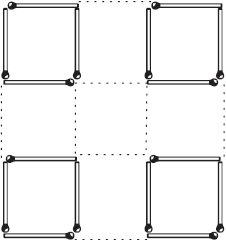 Рис. 11. Рис. 11.
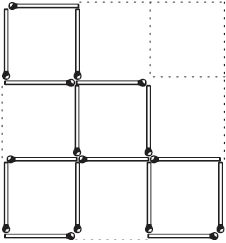 Рис. 12. Рис. 12.
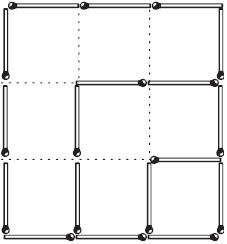 Рис. 13. Рис. 13.
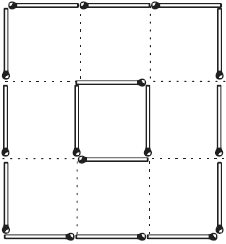 Рис. 14. Рис. 14.
Решение задачи № 16 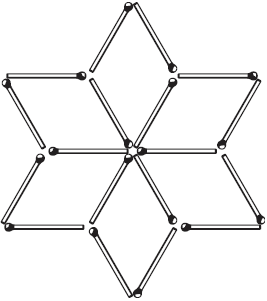
Рис. 15. Решение задачи № 17 показано на чертеже 16-м. Это равносторонний шестиугольник (но не правильный – углы неравны). 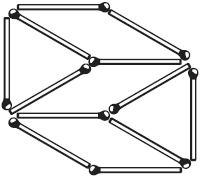
Рис. 16. Решение задачи № 18 показано
на чертеже 17-м. Площадь левой фигуры заключает два квадрата, каждый со
сторонами в 1 спичку. Правый четырехугольник представляет собою
параллелограмм, высота которого AB = 1 1/2спичкам. Площадь его, по
правилам геометрии, равна его основанию, умноженному на высоту: 4x1 1/2 =
6, – т. е. втрое больше площади левого четырехугольника. 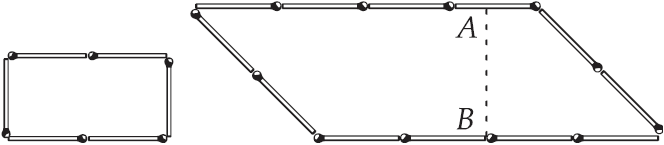
Рис. 17. Решение задач №№ 19 и 20 наглядно показано на прилагаемых чертежах 18 и 19. 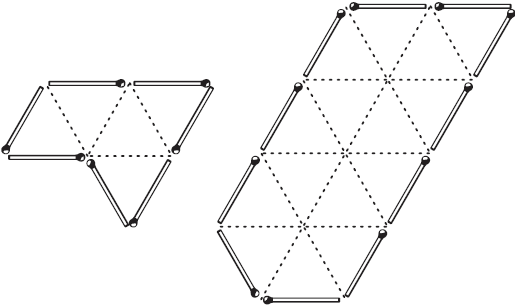
Рис. 18. 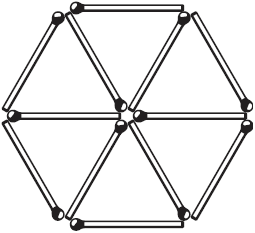 Рис. 19. Рис. 19.
| 
