Мы умеем с помощью циркуля и линейки
делить отрезок только на 2, на 4, на 8 и т. д. число равных частей
(§ 21). Укажем теперь способ делить отрезок на любое число равных
частей.
Пусть потребуется отрезок АВ (черт. 156) разделить на 5 равных частей. Проведем от одного конца этого отрезка, например, от В, под произвольным углом прямую ВС. На этой прямой отложи от конца В пять раз какой-нибудь отрезок; получим точки 1, 2, 3, 4, 5. Последнюю точку 5 соединим с концом А данного отрезка и ч через точ-ки1, 2, 3, 4 проведем прямые, параллельные прямой A5. Можно указать, что эти прямые разделят отрезок АB на 5 равных частей в точках I, II, III, IV.
Для доказательства проведем через точки I, II, III,IV прямые, параллельные ВC (черт. 157). Получим треугольники В1I, ICII, IIDIII, IIIЕIV, IVFА, у которых В—I, I–II, II–III, III–IV, IV—A равны между собою (потому что каждая из них, кроме 1–1, равна противоположной стороне параллелограмма, а В-1, В-2, 2–3, 3–4, 4–5 равны друг другу). Из равенства же указанных треугольников (СУС) вытекает равенство отрезков B-I, 1-11, II–III, III–IV, IV–V.
Применения
Н о н и у с. Ш т а н г е н ц и р к у л ь
Умея делить прямолинейные отрезки на
любое число частей, можно изготовить приспособление, полезное для точных
измерений – так называемый «нониус».
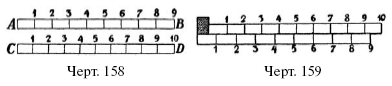
Для примера рассмотрим следующий простейший нониус. Полоску AВ (масштаб, черт. 158) длиною в 9 см разделим на 10 равных частей; по 0,9 см каждая; получим полоску CD(нониус). Пусть теперь требуется измерить длину небольшого предмета М. Прикладываем его к полоскам АВ и CD, как
показывает черт. 159, и замечаем, какие деления обеих полосок
совпадают. Предположим, что совпали 6-е деления. Это показывает, что
длина предмета равна разнице между 6-ю делениями масштаба ПАВ и 6-ю делениями нониуса. Но 6 делений полоски АВ = 6 см, а 6 делений нониуса = 6 0,9 = 5,4 см.
Следовательно, длина предмета равна 6 – 5,4 = 0,6 см. Вообще, длина
измеряемого предмета равна стольким десятым долям деления масштаба,
сколько единиц в совпадающих делениях масштаба и нониуса.
Если бы мы для изготовления нониуса взяли
не 9 сантиметров, а 9 миллиметров, и разделили их общую длину на 10
равных частей, то разность между одним делением масштаба и одним
делением нониуса равнялась бы 0,01 см. Следовательно, помощью такого
нониуса мы могли бы измерять мелкие предметы с точностью до 0,1
миллиметра.
Нониус обычно применяется в форме так
наз. «штангенциркуля», употребляемого для точного измерения мелких
предметов. Иногда нониусом снабжается и «микрометр» – инструмент для
точного измерения толщины.
Сходным образом может быть устроен нониус
для точного измерения дуг. Если 9 градусных делений разделить на 10
частей, то так устроенный нониус позволит измерять дуги с точностью до
0,1 градуса, т. е. до 6.
64. На черт. 160 показано, как можно
воспользоваться метром, чтобы разделить ширину доски на равные части. На
чем этот способ основан?
Р е ш е н и е. Мы имеем в этом случае ряд
параллельных прямых, проведенных через равноудаленные друг от друга
точки одной стороны угла; они должны отсечь от другой стороны угла
(т. е. от края доски) равные отрезки.
65. Середины сторон прямоугольника с
диагональю 10 см последовательно соединены прямыми линиями. Найти обвод
образовавшегося четырехугольника.
Р е ш е н и е. Каждая сторона этого
четырехугольника равна половине диагонали (как линия, соединяющая
середину двух сторон треугольника), т. е. 5 см. Значит обвод
четырехугольника = 20 см.
| 
