|
Другой способ нахождения центра (напр.,
точеных изделий) – помощью особого инструмента, «центроискателя» –
основан на свойствах так наз. касательных линий. К а с а т е л ь н о й к
окружности называется всякая прямая линия, которая в точке встречи с
окружностью перпендикулярна радиусу, проведенному к этой точке.
Например, на черт. 174 прямые АВ, CD и EF– касательные к окружности АСЕ. Точки А, С, Е называются
«точками касания». Особенность касательной, линии та, что она и м е е т
с о к р у ж н о с т ь ю т о л ь к о о д н у о б щ у ю т о ч к у.
Действительно, если бы у касательной AB(черт. 175) была с окружностью, кроме этой еще одна общая точка, напр., С, то, соединив ее с центром, мы получили бы равнобедренный треугольник СОА с двумя прямыми углами СА, а это, мы знаем, невозможно (почему?).
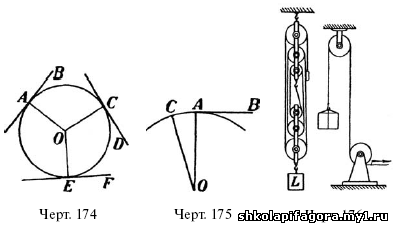
С линиями, касательными к окружности, мы
встречаемся весьма часто в практической жизни. Веревка, перекинутая
через блок, занимает в своих натянутых частях положение касательных
прямых к окружности блока. Ремни талей (сочетания нескольких блоков,
черт. 176) располагаются по линии общих касательных к окружности колес.
Передаточные ремни шкивов тоже занимают положение общих касательных к
окружностям шкивов «внешних» касательных в так наз. открытой передаче и
«внутренних» – в закрытой.
Как через данную точку вне окружности провести к ней касательную? Другими словами: как через точку А (черт. 177) провести прямую АВ, чтобы угол АВО был прямой? Выполняется это следующим образом. Соединяют А с центром О (чертеж 178). Прямую делят пополам и вокруг середины ее В, как центра, описывают окружность радиусом ВО. Иначе говоря, на ОА строят круг, как на диаметре. Точки пересечения С и Dобеих окружностей соединяют с А прямыми линиями: это и будут касательные.
Чтобы в этом убедиться, проведем из центра к точкам С и Dвспомогательные прямые ОС и ОD. Углы ОСА и ODA– прямые, так как они вписаны в полуокружность. А это и значит, что ОС и OD– касательные к окружности.
Рассматривая наше построение, мы видим,
между прочим, что из каждой точки вне окружности можно провести к ней д в
е касательные. Нетрудно убедиться, что обе эти касательные о д и н а к о
в о й д л и н ы, т. е., что AC= AD. Действительно, точка О одинаково удалена от сторон угла А; значит ОА – равноделящая, и следовательно, треугольники ОАС и OADравны (СУС).
Попутно мы установили, что прямая,
которая делит пополам угол между обеими касательными, проходит через
центр круга. На этом основано устройство прибора для разыскания центра
точеных изделий – ц е н т р о и с к а т е л я (черт. 179). Он состоит из
двух линеек АВ и АС, укрепленных под углом, и третьей линейки BD, край которой BDделит пополам угол между краями
первых двух линеек. Прибор прикладывают к круглому изделию так, чтобы прилегающие к нему края линеек АВ и ВС соприкасались
с окружностью изделия. Края будут при этом иметь с окружностью только
по одной общей точке, поэтому край линейки должен, согласно сейчас
указанному свойству касательных, пройти через центр круга. Прочертив на
изделии по линейке диаметр круга, прикладывают центроискатель к изделию в
другом положении и прочерчивают другой диаметр. Искомый центр окажется
на пересечении обоих диаметров.
Если нужно провести общую касательную к
двум окружностям, т. е. провести прямую линию, которая касалась бы
одновременно двух окружностей, то поступают следующим образом. Около
центра одной окружности, например, около В (черт. 180), описывают вспомогательную окружность радиусом, равным разности радиусов обеих окружностей. Затем из точки А проводят касательные АС и AD к этой вспомогательной окружности. Из точек А и В проводят прямые, перпендикулярные к АС и AD, до пересечения с данными окружностями в точках E, F, H и G. Прямые, соединяющие Е с F, G с H, будут общие касательные к данным окружностям, так как они перпендикулярны к радиусам AE, CF, AG и DH.
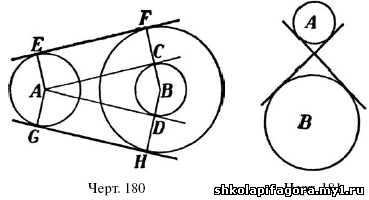 Кроме тех двух касательных, которые
сейчас были проведены и которые называются в н е ш н и м и, возможно еще
провести две другие касательные, расположенные так, как на черт. 181 (в
н у т р е н н и е касательные). Чтобы выполнить это построение,
описывают вокруг центра одной из данных окружностей – например, вокруг В – вспомогательную окружность радиусом, равным с у м м е радиусов обеих окружностей. Из точки А проводят к этой вспомогательной окружности касательные. Дальнейший ход построения читатели смогут найти сами.
Повторительные вопросы
Что называется касательной? Сколько общих
точек у касательной и окружности? – Как провести касательную к
окружности через точку, лежащую вне окружности? – Сколько можно провести
таких касательных? – Что такое центроис-катель? – На чем основано его
устройство? – Как провести общую касательную к двум окружностям? –
Сколько таких касательных?
Применения
71. Два прямых участка дороги соединены
дугою так, что прямые участки имеют направление касательных к этой дуге
(черт. 182). Угол между прямыми участками – 155°. Найти длину дуги, если
радиус ее = 270 метров.
Р е ш е н и е. Из черт. 182 видим, что в четырехугольнике ОВЕС уг. Е – 155°, уг. ОBE – прямой, уг. ОСЕ – прямой. Так как сумма внутренних углов четырехугольника = 180° [4 – 2] – 360°, то угол О =
360° – [155° + 90° + 90°] – 25°. Длина полной окружности радиуса 270 м –
2 ? 3,14 ? 270 = 1700 м, а длина дуги в 25°= 1700 ? 25/360 = 120 м.
Искомая длина дуги – 120 метров.
| 
