О круглых изделиях, суживающихся по
прямой линии к одному концу, говорят, что они имеют «конусность».
Конусность измеряется величиною уменьшения радиуса круга поперечного
сечения на каждый сантиметр длины изделий. Если, например, радиус круга
поперечного сечения изделия уменьшается с каждым сантиметром на 0,25 мм,
то конусность изделия равна 0,25 мм на 1 см.
Легко рассчитать, что если длина изделия – 40 см, то от одного конца к другому оно суживается на 2 0,25 мм 40 = = 20 мм = 2 см.
Наоборот, если круглое изделие в 50 см длины имеет на концах разность
толщины (диаметров) 30 мм, то на каждый сантиметр длины разность
диаметров составляет 30 мм: 50 = 0,6 мм, а разность радиусов – 0,3 мм;
значит «конусность» этого изделия 0,3 мм на 1 см (или 0,3: 10 = 0,03).
Итак, конусность измеряется отношением катетов (черт. 227) ВС : АС в прямоугольном треугольнике АВС. Это отношение определяет наклон прямой АВ к LCи, следовательно, может служить мерою угла ВАС.
Мы видим из этого примера, что кроме уже
известного нам градусного способа измерения острых углов, можно
пользоваться еще и другим способом. Способ этот состоит в том, что за
меру острого угла принимают отношение противолежащего ему катета к
прилежащему катету в том треугольнике, который отсекается от этого угла
перпендикуляром к одной из сторон. Например, угол А (черт. 228) можно измерять отношением ВС : АВ или равным ему отношением ED: AE (почему эти отношения равны?), или также равным им отношением MN: AN (почему это отношение равно предыдущим?). Каждое из этих равных отношений называется т а н г е н с о м угла A и обозначается через tang или tg.
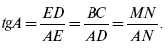
Легко понять, что каждому острому углу
отвечает определенный тангенс. Найти значение тангенса для каждого угла
возможно помощью чертежа, измерив длину соответствующих линий и вычислив
их отношение. Таким путем можно составить таблицу тангенсов для всех
углов от 1° до 10°. Способ этот прост, но не достаточно точен.
Существуют способы (чересчур сложные, чтобы их рассматривать здесь)
узнавать тангенсы с любою точностью посредством вычислений. Готовая
таблица вычисленных таким путем тангенсов для всех острых углов от 0°до
90° приложена в конце книги (вместе с некоторыми другими величинами, о
которых речь будет дальше).
Если станем изменять величину угла от 0°
до 90° и следить, как изменяется при этом величина тангенса, то заметим
следующее. Когда угол близок к 0°, то и тангенс близок к нулю; поэтому
условно пишут, что tg0° = 0. С увеличением угла tgего
быстро возрастает, а при 90° перпендикуляр к одной стороне угла вовсе не
встречает другой: точка пересечения, как говорят, «удаляется в
бесконечность». Поэтому считают, что tg90 ° = бесконечности.
Для некоторых углов можно вычислить тангенс весьма несложным расчетом. Например, тангенс угла в 45° равен (черт. 229) ВС : АВ = 1 (почему?). Тангенс угла в 30° (черт. 230) равен ВС: АВ; но в треугольнике АСВ
Вместо отношения противолежащего катета к
прилежащему можно для измерения острых углов брать и обратное отношение
прилежащего катета к противолежащему. Это отношение называется к о т а н
г е н с о м угла и обозначается знаком cotg. Из черт. 228 имеем:
Вообще между тангенсом и котангенсом существует следующая зависимость:
Легко сообразить, что с увеличением угла тангенс его увеличивается, а котангенс – уменьшается.
Рассмотрим еще одну зависимость между величиною тангенса и котангенса острых углов. Из прямоугольного треугольника АВС (черт. 231) видим:
А так как сумма углов А и В равна 90° (эти углы, как принято говорить, «дополнительные»), то tg А= cotg (90 – A); cotg A = tg (90 – А).
Например:
tg30° = cotg60°; tg17° = cotg73° и т. п.
Выражая эту зависимость словесно, устанавливаем правило:
т а н г е н с о с т р о г о у г л а р а в е н к о т а н г е н с у д о п о л н и т е л ь н о г о у г л а.
На этом основании таблицу тангенсов и
таблицу котангенсов углов можно свести в одну таблицу, устройство
которой мы сейчас объясним.
| 
