Пирамидой называется тело, ограниченное с
одной стороны треугольником или каким-нибудь многоугольником (о с н о в
а н и е пирамиды), а со всех других сторон – треугольниками,
сходящимися в одной точке (в вершине пирамиды). Перпендикуляр,
проведенный от вершины пирамиды к ее основанию, называется ее высотою
(прямая называется п е р п е н д и к у л я р н о й к п л о с к о с т и,
если она составляет прямые углы с каждой прямой, проведенной в этой
плоскости через точку встречи). Если основание пирамиды – треугольник,
пирамида называется «треугольной», если четырехугольник –
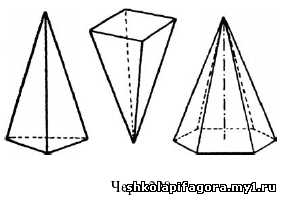
«четырехугольной» и т. д. На черт. 238 изображены треугольная,
четырехугольная и шестиугольная пирамиды.
Если мы начертим развертку какой-нибудь
пирамиды (сделайте это), то установим способ вычисления ее б о к о в о й
поверхности: надо вычислить площадь каждой боковой треугольной грани и
все эти площади сложить. В том случае когда все боковые грани одинаковы
(такая пирамида называется п р а в и л ь н о ю), вычисление упрощается:
определяют площадь одной треугольной грани и умножают ее на число
граней. Например, боковая поверхность правильной шестиугольной пирамиды
равна 6 ? al/2 =3al,
где a– сторона шестиугольника, лежащего в основании пирамиды, а l – высота каждой треугольной грани; она называется «апофемой» правильной пирамиды. Для правильной пирамиды о nгранях боковая поверхность равна n ? al/2 = nal/2
Так как па – есть сумма сторон
основания пирамиды, т. е. ее периметр, то правило вычисления боковой
поверхности правильной пирамиды можно словесно высказать так:
б о к о в а я п о в е р х н о с т ь п р а
в и л ь н о й п и р а м и д ы р а в н а п о л у п р о и з в е д е н и ю
п е р и м е т р а о с н о в а н и я н а а п о ф е м у. Правило
вычисления объема пирамиды выводится в подробных учебниках математики.
Мы приведем его здесь без доказательства, так как доказательство это
чересчур сложно:
о б ъ е м п и р а м и д ы р а в е н о д н о й т р е т и п р о и з в е д е н и я е е о с н о в а н и я н а в ыс о т у.
Обозначив площадь основания пирамиды через S, а высоту через A, получим такую формулу объема и пирамиды:
V= 1/3 Sh.
Повторительные вопросы
Что называется пирамидой? – Что
называется основанием и что – вершиной? – Что называется высотою
пирамиды? – Какая пирамида называется пятиугольной, десятиугольной,
12-угольной? – Какая пирамида называется правильной? – Что называется
апофемой правильной пирамиды? – Припомните, что называется апофемой
правильного многоугольника. – Как вычисляются боковая поверхность и
объем правильной пирамиды? – Как выражаются эти правила формулами? – Как
выражаются эти правила формулами?
Применения
117. Величайшая из пирамид Египта
(пирамида Хеопса) достигала в высоту 146 метров; ее квадратное основание
имело 233 метра в ширину. Предполагая, что она сплошь сложена из
камней, вычислите, какой высоты каменную стену, толщиною в полметра и
длиною от Ленинграда до Москвы, можно было бы соорудить из ее материала
(расстояние – 640 километров).
Р е ш е н и е. Объем пирамиды равен
1/3 ?2332?146 куб. м.
Обозначив искомую высоту стены через x, имеем уравнение
6 400 000 ??? х = 1/32332-146, откуда х = 8,5 м.
118. Стог соломы имеет форму
прямоугольного параллелепипеда с пирамидальной верхушкой. Размеры
основания стога 6 Ч 6 м; высота до основания пирамиды – 4 м до верши-1
ны пирамиды – 5 м. Сколько килограммов соломы в этом стоге? Куб. метр
соломы весит 100 кг.
Р е ш е н и е. Объем призматической части
стога 6 ? 6 ? 4 = 144 куб. м. Объем пирамидальной части 1/3 ? 6 ? 6 =
12 куб. м. Общий объем 144 + 12 = 156 куб. м. В стоге 15 600 кг соломы.
119. Вычислите объем и боковую
поверхность правильной пятигранной пирамиды, сторона основания которой
45 см, а высота – 76 см.
Р е ш е н и е. Начнем с вычисления
площади основания пирамиды, при чем воспользуемся тригонометрическими
соотношениями. Площадь правильного пятиугольника со стороною 45 см равна
5 ? 45 ? ? l,
где l – апофема. Так как центральный угол, опирающийся на сторону правильного вписанного пятиугольника, = 360°/5 = 72°, то апофема l = 22, cotg 36° = 16 см. Следовательно, площадь основания пирамиды 5 45 8 = 1800 кв. см, а искомый объем = 1/31800 ? 76 = 45 600 куб. см.
Для вычисления боковой поверхности
необходимо определить длину апофемы пирамиды. Из чертежа (сделайте его)
видно, что апофема есть гипотенуза прямоугольного треугольника, катеты
которого – высота пирамиды и апофема ее
основания. Значит, апофема пирамиды
Отсюда боковая поверхность пирамиды 6 ? 145 ? ? ?78 = 10 000 кв. см.
| 
