|
Фигуры, ограниченные более чем 4-мя
линиями, назы ваются м н о г о у г о л ь н и к а м и (черт. 96). Прямые,
соединяющие две несоседние вершины многоугольника, называются д и а г о
н а л я м и (черт. 96, b). Так как всякий многоугольник можно
разбить диагоналями на треугольники, то площадь многоугольника легко
вычислить, найдя площадь каждой его треугольной части.
Если, например, план участка имеет форму
многоугольника, то, проведя в нем диагонали, измеряют длину оснований и
высот образовавшихся треугольников. По этим данным определяют площадь
каждого треугольника, а зная это, вычисляют площадь составляемого ими
многоугольника.
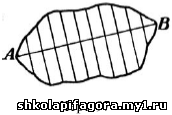
При измерении площади участка,
ограниченного линией неправильной формы, приходится довольствоваться
лишь приближенным результатом. Пусть требуется определить площадь
фигуры, изображенной на черт. 97. Для этого проводят прямую АВ и
через равные расстояния – к ней перпендикуляры. Фигура будет разрезана
ими на узкие полосы, каждую из которых можно рассматривать как трапецию.
Измерив параллельные стороны каждой трапеции, а также высоту
(одинаковую для всех, потому что перпендикуляры проведены на равных
расстояниях), вычисляют их площади; сумма отдельных площадей приближенно
равна площади данной фигуры. Чем ближе проведены друг к другу
перпендикуляры, тем точнее определение площади всей фигуры.
В некоторых случаях можно определить
приближенно площадь фигуры посредством в з в е ш и в а н и я. Если,
например, фигура, площадь которой требуется определить, начерчена на
картоне, то, вырезав ее, узнают тщательным взвешиванием, во сколько раз
эта фигура тяжелее сантиметрового квадрата из того же картона; во
столько же раз, очевидно, больше и площадь.
| 
