|
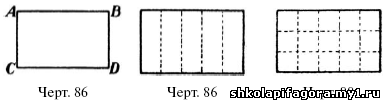
Пусть требуется определить площадь какого-нибудь прямоугольника, например, ABDC(черт.
86). Измеряют линейной единицей, напр. метром, длину этого участка.
Предположим, что метр укладывается в длине 5 раз. Разделим участок на
поперечные полоски шириною в метр, как показано на черт. 87. Таких полос
получится, очевидно, 5. Далее измерим метром ширину участка; пусть она
равна 3 метрам. Разделим участок на продольные полосы в 1 метр ширины,
как показано на черт. 88; их получится, конечно, 3. Каждая из пяти
поперечных полос рассечется при этом на 3 квадратных метра, а весь
участок будет разделен на 5 Ч 3=15 квадратов со стороною в 1 метр: мы
узнали, что участок заключает в себе 15 кв. метров. Но мы могли получить
то же число 15, не разграфляя участка, а только перемножив его длину на
его ширину. Итак, чтобы узнать, сколько квадратных метров в
прямоугольнике, нужно измерить его длину, его ширину и перемножить оба
числа.
В рассмотренном случае единица длины –
метр – укладывалась в обеих сторонах прямоугольника ц е л о е число раз.
В подробных учебниках математики доказывается, что установленное сейчас
правило верно и тогда, когда стороны прямоугольника не содержат целого
числа единиц длины. Во всех случаях:
П л о щ а д ь п р я м о у г о л ь н и к а р а в н а
п р о и з в е д е н и ю е г о д л и н ы н а ш и р и н у,
и л и, к а к г о в о р я т в г е о м е т р и и, – е г о
«о с н о в а н и я» н а е г о «в ы с о т у».
Если длина основания прямоугольника обозначена буквою а, а длина высоты – буквою b, то площадь его S равна
S = a ? b,
или просто S= ab, потому что знак умножения между буквами не ставится.
Легко сообразить, что для определения
площади к в а д р а т а надо умножить длину его стороны на себя, т. е.
«возвысить в квадрат». Другими словами:
П л о щ а д ь к в а д р а т а р а в н а к в а д р а т у е г о с т о р о н ы. Если длина стороны квадрата а, то площадь его S равна
S= a ? a= a2.
Зная это, можно установить соотношение
между различными квадратными единицами. Например, в квадратном метре
содержится квадратных дециметров 10 Ч 10, т. е. 100, а квадратных
сантиметров 100 Ч 100, т. е. 10 000, – потому что линейный сантиметр
укладывается в стороне квадратного дециметра 10 раз, а квадратного
метра-100 раз.
Для измерения земельных участков
употребляется особая мера – г е к т а р, содержащая 10 000 квадратных
метров. Квадратный участок со стороною 100 метров имеет площадь в 1
гектар; прямоугольный участок с основанием 200 метров и высотою 150
метров имеет площадь 200 Ч 150, т. е. в 30 000 кв. м или 3 гектара.
Обширные площади – например, округа и районы, – измеряются
к в а д р а т н ы м и к и л о м е т р а м и.
Сокращенное обозначение квадратных мер таково:
квадр. метр………………………………. кв. м или м2
квадр. дециметр…………………………. кв. дм или дм2
квадр. сантиметр………………………… кв. см или см2
квадр. миллиметр……………………….. кв. мм или мм2
гектар…………………………………….. га
Повторительные вопросы
Как вычисляется площадь прямоугольника?
Квадрата? – Сколько кв. см в кв. м? Сколько кв. мм в кв. м? – Что такое
гектар? – Сколько гектаров в кв. км? Как сокращенно обозначают
квадратные меры?
Применения
20. Требуется окрасить иол комнаты,
изображенный на черт. 6. Размеры, обозначены в метрах. Сколько
понадобится для этого материалов и рабочей силы, если известно, что для
окраски одного кв. метра деревянных полов с замазкой щелей и сучьев по
прежде окрашенному, за два, требуется (по Урочному Положению):
Маляров…………………………………….. 0,044
Олифы, килограммов…………………….… 0,18
Охры светлой, кг…………………………… 0;099
Замазки, кг…………………………………0,00225
Пемзы, кг………………………………….. 0,0009.
Р е ш е н и е. Площадь пола равна 8 ? 12 = 96 кв. м.
Расход материалов и рабочей силы таков
Маляров. . . . . . . . 0,044 ? 96 = 4,2
Олифы. . . . . . . . 0,18 ? 96= 17 кг
Охры. . . . . . . . . 0,099 ? 96 – 9,9 кг
Замазки. . . . . . . . 0.00225 ? 96 = 0,22 кг
Пемзы. . . . . . . . . 0,0009 ? 96 = 0,09 кг.
21. Составьте ведомость расхода рабочей
силы и материалов для оклейки обоями комнаты предыдущ. задачи. На
оклейку стен простыми обоями с бордюрами требуется (по Уроч. Положению)
на кв. метр:
Маляров или обойщиков………………………… 0,044
Обоев (шир. 44 см) кусков……………………… 0,264
Бордюр (по расчету)
Крахмала граммов………………………………. 90.
Р е ш е н и е – по образцу, указанному в
предыдущей задаче. Заметим лишь, что при подсчете необходимого
количества обоев на практике отверстия стен из их площади не вычитают
(так как при пригонке фигур в смежных полотнищах часть обоев теряется).
| 
