|
Рассмотрим сначала, как вычисляется
площадь п р ям о у г о л ь н о г о треугольника. Пусть требуется
определить площадь треугольника ABC(черт. 89), в котором угол В – прямой. Проведем через вершины А и С прямые, параллельные противолежащим сторонам. Получим (черт. 90) прямоугольник ABCD(почему эта фигура – прямоугольник?), который делится диагональю АС на два равные треугольника (почему?). Площадь этого прямоугольника равна ah; площадь же нашего треугольника составляет половину площади прямоугольника, т. е. равна 1/2 ah. Итак, площадь всякого прямоугольного треугольника равна половине произведения его сторон, заключающих прямой угол.
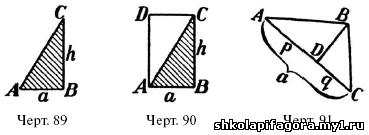 Пусть теперь требуется определить площадь треугольника косоугольного (т. е. не прямоугольного), – напр. ABC(черт.
91). Проводим через одну из его вершин перпендикуляр к противоположной
стороне; такой перпендикуляр называется в ы с о т о ю этого
треугольника, а сторона, к которой он проведен – о с н о в а н и е м
треугольника. Обозначим высоту через h, а отрезки, на которые она делит основание, через pи q. Площадь прямоугольного треугольника ABD, как мы уже знаем, равна 1/2 ph; площадь ВDC = 1/2 qh. Площадь S треугольника ABC равна сумме этих площадей: S = 1/2 ph+ 1/2 qh= 1/2 h(р + q). Но р + q = а; следовательно S= 1/2 ah.
Рассуждение это нельзя прямо применить к
треугольнику с тупым углом (черт. 92), потому что перпендикуляр CD
встречает не основание АВ, а его продолжение. В этом случае приходится рассуждать иначе. Обозначим отрезок AD через p, BD– через, q, так что основание а треугольника равна p– q. Площадь нашего треугольника АВС равна р а з н о с т и площадей двух треугольников ADC– BDC= 1/2 ph– 1/2 qh= 1/2 h(p– q) = 1/2 ah.
Итак, во всех случаях площадь треугольника равна половине произведения любого его основания на соответствующую высоту.
Отсюда следует, что треугольники с равными основаниями и высотами имеют одинаковые площади, или, как говорят,
р а в н о в е л и к и.
Равновеликими вообще называются фигуры,
имеющие равные площади, хотя бы сами фигуры не были равны (т. е. не
совпадали при наложении).
Повторительные вопросы
Что называется высотою треугольника?
Основанием треугольника? – Сколько высот можно провести в одном
треугольнике? – Начертите треугольник с тупым углом и проведите в нем
все высоты. – Как вычисляется площадь треугольника? Как выразить это
правило формулой? – Какие фигуры называются равновеликими?
Применения
22. Огород имеет форму треугольника с
основанием 13,4 м и высокою 37,2 м… Сколько (по весу) требуется семян,
чтобы засадить его капустой, если на кв. м идет 0,5 грамма семян?
Р е ш е н и е. Площадь огорода равна 13,4 ? 37,2 = 498 кв. м.
Семян потребуется 250 г.
23. Параллелограмм разбивается диагоналями на 4 треугольные части. Какая из них имеет наибольшую площадь?
Р е ш е н и е. Все 4 треугольника равновелики, так как имеют равные основания и высоты.
| 
