Сравнивая между собою фигуры, мы
различали до сих пор только два случая: случай равенства фигур и случай
их неравенства. Но возможен и третий случай, которого мы еще не
рассматривали: фигуры не равны, а п о х о ж и, так что одна представляет
уменьшенное п о д о б и е другой. Например, большой и малый квадрат не
равны, но имеют совершенно одинаковую форму: один представляет подобие
другого (черт. 185). Два равносторонних треугольника, большой и малый,
также имеют одинаковую форму (черт. 186).
Такие фигуры, которые имеют различную величину сторон, но одинаковы по форме, называются п о д о б-н ы м и фигурами.
В каком же случае считаем мы, что у двух
фигур одинаковая форма? Рассмотрим этот вопрос для двух многоугольников.
Для одинаковости формы многоугольники должны прежде всего иметь
соответственно равные углы. Если углы одного многоугольника не равны
углам другого, мы не назовем эти фигуры одинаковыми по форме (см. фигуры
черт. 188). Значит, равенство углов одной фигуры углам другой есть
необходимое условие для одинаковости их формы, т. е, для п о д о б и я
этих фигур. Но д о с т а т о ч н о ли одного этого условия? Всякие ли
две фигуры с соответственно равными углами имеют одинаковую форму?
Взгляните на прямоугольники черт. 187. Углы прямоугольника I равны углам
прямоугольника II, – однако, мы не скажем, что они одинаковой формы.
Почему?
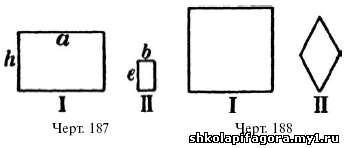
Потому что высота первого больше высоты
второго в 2 раза, а основание первого больше основания второго в 5 раз.
Стороны этих фигур, как говорят, не п р о п о р ц и о н а л ь н ы: из
них нельзя составить пропорции (отношение двух из них не равно отношению
двух других). Форма этих четырехугольников была бы одинакова только
тогда, когда из их «сходственных» сторон (т. е. из сторон, прилегающих к
равным углам) можно составить пропорцию
a/b – h/l
Короче мы можем высказать это условие подобия многоугольников так:
м н о г о у г о л ь н и к и п о д о б н
ы, к о г д а и х с х о д с т в е н н ы е с т о р о н ы п р о п о р ц и о
н а л ь н ы (т. е.
о т н о ш е н и е д в у х и з н и х р а в
н о о т н о ш е н и ю д в у х д р у г и х). Стороны многоугольников
могут быть пропорциональны и не будучи сходственными, т. е. не прилегая к
равным углам. Например, на черт. 188 каждая сторона квадрата I вдвое
длиннее каждой стороны ромба II; значит, стороны этих фигур
пропорциональны. Но все-таки эти фигуры не подобны, потому что
пропорциональные стороны их не прилегают к равным углам: они не
сходственные.
Итак, для подобия, например, многоугольников ABCDE и A1B1C1D1E1 (черт. 189) необходимо:
чтобы
уг. A = уг. A1
уг. B = уг. B1
уг. C = уг. C1
уг. D = уг. D1
уг. E = уг. E1
и, во-вторых, чтобы
(А1– читается «А прим», или «А со знаком»).
| 
