Первым коммерчески успешным калькулятором был арифмометр, созданный французом Шарлем Ксавье Тома де Кольмаром (1785–1870). Он успешно продавался не только во Франции, но и в других странах. Конкуренты не дремали, и через несколько лет было создано несколько альтернативных моделей. Наиболее заметными были калькулятор «Арифморель» еще одного француза Тимолеона Мореля (1842), калькулятор с зубчатыми колесами, созданный американцем Фрэнком Болдуином (1872), который независимо от него также был разработан шведом Вильгодтом Однером (1874), жившим в Санкт-Петербурге, а также круговой калькулятор англичанина Джозефа Эдмондсона (1885). Все эти машины использовались даже в первые годы XX века.

Устройство «Арифмореля» — калькулятора, созданного Тимолеоном Морелем.

Начиная с машины Мореля в калькуляторах помимо основных арифметических операций появилась возможность вычисления квадратных корней. Квадратные корни вычислялись на основании следующего разложения в ряд для функции х²:

1 + 3 + 5 + … + (2х — 1) = х².

Для данного числа n, которое является полным квадратом, квадратный корень из n можно получить последовательным вычитанием из него чисел 1, 3, 5, пока результат вычитания не станет равен нулю. Число выполненных операций вычитания будет равно квадратному корню исходного числа. Допустим, мы хотим вычислить квадратный корень из 100. Нужно последовательно вычесть из него 1, 3, 5, 7, 9, 11, 13, 15, 17, 19. Так как мы вычли из 100 десять чисел, квадратный корень из 100 равен 10.

Если n не является полным квадратом, результатом последнего вычитания будет отрицательное число. Число выполненных операций вычитания будет приближенно равно истинному значению квадратного корня. Чтобы получить искомое значение с точностью до нескольких десятичных знаков, вышеуказанный процесс нужно повторить. При этом для каждого нового десятичного знака исходное число следует умножить на 100 в следующей степени. Например, умножим 2 на 100, чтобы вычислить квадратный корень из 200 и получить один знак после запятой. Имеем:

1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 =

= 196 < 200 < 225 =

= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29.

Заметим, что в верхнем ряду складывается 14 слагаемых, в нижнем — 15.

Следовательно, квадратный корень из 200 находится между 14 и 15, корень из 2 — между 1,4 и 1,5.

В XIX веке были совершены открытия, которые подготовили почву для развития современных информационных технологий. В 1835 году американский физик Джозеф Генри, известный работами по электромагнетизму, изобрел электромеханическое реле.

Еще одно открытие — появление цифровой клавиатуры — предвосхитило основу интерфейса будущих компьютеров. До этого в калькуляторах использовались особые способы ввода множителей, что также требовало особой подготовки в области вычислений. Открытие клавиатуры сделало калькуляторы доступными для всех.

С массовым внедрением промышленных решений автоматические вычисления стали идти параллельным курсом с автоматизацией текстильной промышленности.

Француз Базиль Бушон уже в 1725 году создал перфорированную ленту для программирования ткацкого станка, на которой содержалась информация об узорах на ткани. Лента помещалась в станок, и постепенно получалась ткань с заданным узором. Несколько лет спустя, в 1728 году, помощник Бутона Жан-Батист Фалькон усовершенствовал его систему и заменил ленту перфорированными картами. В 1803 году Жозеф Мари Жаккар (1752–1834) создал знаменитый автоматический станок Жаккара на основе системы инженера Жака де Вокансона, в которой использовались карты и вращающийся барабан. Автоматический станок Вокансона, созданный в 1740 году, работал под управлением одного оператора. Система, в которой использовались перфокарты, наиболее эффективная на тот момент, непрерывно развивалась и позднее стала применяться в компьютерах XX века. Статистик Герман Холлерит (1860–1929) использовал перфокарты для кодирования результатов переписи населения США 1890 года. Холлерит был первым, кому удалось обработать информацию автоматически, поэтому он считается создателем информатики (это слово образовано слиянием слов «информация» и «автоматика»).

Перфокарты в станке Жаккара, представленном в Музее науки и промышленности в Манчестере.

Чарльз Бэббидж

Английский философ, математик, изобретатель и инженер Чарльз Бэббидж, считающийся изобретателем вычислительных машин, — один из самых выдающихся и противоречивых героев нашей истории. Он родился на окраине Лондона предположительно в 1791 году; достоверно известна лишь дата его крещения — 6 января 1792 года, в церкви Сент-Мэри в Ньюингтоне. Он изучал математику и химию — сначала в Кембриджском Тринити-колледже, куда поступил в 1810 году, затем в менее крупном и престижном колледже Петерхаус (1812). Считается, что Бэббидж сменил колледж потому, что двое его близких друзей по Тринити-колледжу Джон Гершель и Джордж Пикок превосходили его в учебе, а в Петерхаусе он стал первым учеником. В 1814 году он получил степень бакалавра, в 1817 — степень магистра математики.

Потрет Чарльза Бэббиджа кисти Сэмюэля Лоренса.

В 1812 году Бэббидж, Гершель и Пикок с коллегами под руководством профессора Роберта Вудхауза основали Аналитическое общество. Их целью было распространение аналитического исчисления Лейбница и противостояние анализу Ньютона.

Наиболее значимым достижением общества стал перевод с французского книги Сильвестра Франсуа Лакруа Traite de calcul differentiel et integral («Трактат о дифференциальном и интегральном исчислении», 1816), а также введение Пикоком нотации Лейбница на некоторых экзаменах (1817). Трехтомный труд Лакруа, переведенный Бэббиджем, Гершелем и Пикоком, получил широкое распространение в Англии. В 1819 году общество стало называться Кембриджским философским обществом.

В год окончания университета (1814) Бэббидж женился на Джорджиане Витмор. У них было восемь детей. Когда его отец, жена и ребенок умерли в 1827 году, Бэббидж получил в наследство недвижимость и солидную сумму, однако чувствовал себя совершенно разбитым и подавленным. По совету врача он на год отправился в путешествие по Европе. По возвращении он занял должность профессора Кембриджского университета, ранее принадлежавшую Ньютону. Однако он счел жалование невысоким и появлялся в университете, только когда требовалось оценить кандидатов на премию Смита, которая вручалась лучшему студенту Кембриджа.

Чарльз Бэббидж вошел в историю как создатель механических вычислительных машин. Первой из них была разностная машина (Difference Engine), которую он создал для вычисления значений многочленов. Принцип ее действия был основан на использовании конечных разностей, что позволило избежать умножения и деления. Изготовление машины было начато в 1822 году при поддержке британского правительства, однако этот проект так и не был завершен. Работы над машиной остановились в 1834 году, когда было прекращено финансирование проекта.

Изображение разностной машины Чарльза Бэббиджа, опубликованное в журнале Harper's Magazine в декабре 1864 года.

Некоторые исследователи считают, что машина Бэббиджа не могла быть закончена из-за существовавших на тот момент технических ограничений. Однако швед Георг Шутц (1785–1873) и его сын Эдвард, прочитав статью о разностной машине Бэббиджа, создали свой вариант этой машины и представили его в 1843 году.

Позднее, в 1851 году, при поддержке Шведской академии наук они построили машину большего размера, способную выполнять вычисления с точностью до 15 знаков после запятой и печатать результаты расчетов.

В отличие от Чарльза Бэббиджа, который не смог завершить работу над своей машиной, Шутц создал полностью рабочий экземпляр. В 1991 году в лондонском Музее науки был воссоздан первый прототип машины Бэббиджа с использованием технологий того времени. Также был воссоздан второй прототип, который в настоящее время хранится в Музее компьютерной истории в городе Маунтин-Вью (штат Калифорния, США). Машина Бэббиджа позволяла выполнять расчеты с точностью до 31 знака, вычислять значения многочленов седьмой степени и имела размеры 2,4 X 2,1 X 0,9 м. Размеры машины Шутца составляли 54 X 86 X 65 см, однако она была способна вычислять значения многочленов всего лишь третьей степени с точностью до 15 знаков. В 2000 году в лондонском Музее науки также была построена печатная машина, спроектированная Бэббиджем для своей вычислительной машины.

Оставив работу над разностной машиной в 1834 году, Бэббидж занялся новым устройством, которое он назвал аналитической машиной (Analytical Engine). Аналитическая машина стала ближайшим предком современных компьютеров. С помощью разностной машины можно было вычислять лишь значения многочленов, в то время как аналитическая задумывалась как устройство широкого применения, способное вычислять значения произвольных функций. Источником энергии для новой машины Бэббиджа служил паровой двигатель, ввод информации выполнялся с помощью перфокарт, вывод — с помощью печатной машины и устройства для нанесения перфорации на перфокарты. В памяти машины могло храниться до тысячи 50-значных чисел. Она также содержала арифметическое устройство для выполнения четырех основных действий, которое Бэббидж назвал мельницей (the mill).

Для программирования машины использовался особый язык, ставший прообразом современных языков программирования. Помимо базовых инструкций этот язык содержал операторы циклов, условные операторы и инструкции для хранения данных. С формальной математической точки зрения машина Бэббиджа была эквивалентна машине Тьюринга, появившейся век спустя.

Бэббидж работал над машиной совместно с Адой Лавлейс, дочерью лорда Байрона. Ее вклад был по достоинству оценен позднее, и теперь Ада Лавлейс считается первым программистом в истории. Она предвидела, что в будущем компьютеры будут использоваться не только для численных расчетов, в то время как Бэббидж уделял основное внимание именно им.

* * *

АДА БАЙРОН, ГРАФИНЯ ЛАВЛЕЙС (1815–1852)

Ада Августа Байрон была единственной дочерью лорда Байрона и Анабеллы Милбэнк. Девочка не знала отца, так как родители разошлись за месяц до ее рождения, и лорд Байрон навсегда покинул Англию. Она была болезненным ребенком (слабое здоровье она унаследовала от отца), поэтому обучалась на дому. Особое внимание при этом уделялось математике и другим наукам. Ее обучали известные преподаватели: Уильям Френд, Уильям Кинг, Мэри Сомервилл и Огастес де Морган. Учителя считали, что девочка сможет стать исследователем первой величины. Мэри Сомервилл представила ее Чарльзу Бэббиджу. В знак признания ее заслуг по созданию языков программирования Министерство обороны США назвало в ее честь язык программирования Ада.

* * *

Они начали сотрудничать, когда Бэббидж попросил Аду Байрон перевести с французского текст Луиджи Менабреа об аналитической машине, написанный вскоре после выступления Бэббиджа в Турине, куда его пригласил математик Джованни Плана. Ада дополнила статью Менабреа примечаниями, которые по объему превысили исходный текст. В знаменитом примечании G помимо других важнейших открытий описывается алгоритм вычисления чисел Бернулли на языке программирования машины Бэббиджа с помощью двух циклов. Так было доказано, что машина Бэббиджа может иметь самое широкое применение. Это была первая в мире компьютерная программа. Ада также описала алгоритмы вычисления тригонометрических функций, в которых использовались переменные.

* * *

* * *

Некоторые исследователи высказывают сомнения относительно того, кто был автором примечания G. Быть может, это был сам Бэббидж? Как бы то ни было, бесспорно, Ада обладала обширными знаниями математики и была знакома с принципом действия аналитической машины. Она настолько тесно сотрудничала с ее изобретателем, что ее вклад в разработку аналитической машины трудно переоценить.

Ада превосходно разбиралась в устройстве станка Жаккара, и некоторые авторы считают, что именно она подсказала Бэббиджу, что для ввода программ и данных в аналитическую машину можно использовать перфокарты. Ада сформулировала понятия инструкций, циклов и подпрограмм, которые известны каждому, кто знаком с языками программирования. За ее талант и знания математики Бэббидж называл ее «повелительницей чисел» (the Enchantress of Numbers).

Аналитическая машина также не была сконструирована полностью, на этот раз из-за возникших финансовых, политических и юридических проблем. Были разработаны лишь некоторые компоненты, в частности элементы арифметического устройства и системы печати. Ни память, ни программируемые компоненты созданы не были.

Компьютеры, сопоставимые по логическому устройству с этой машиной, были созданы лишь 100 лет спустя. Аналитическая машина была забыта всеми, за исключением некоторых изобретателей, на которых оказали влияние важнейшие понятия, сформулированные Бэббиджем в ходе работы над ней.

В 1903 году ирландский бухгалтер Перси Ладгейт спроектировал машину, схожую с машиной Бэббиджа, в которой на смену паровому двигателю пришел электромотор. Испанский инженер, математик и автор множества изобретений Леонардо Торрес Кеведо использовал идеи Бэббиджа при создании автоматической шахматной машины в 1911 году. Его машина была способна играть с человеком окончание шахматной партии с королем и ладьей против короля. Машина действовала не совсем точно, но всегда ставила мат за минимально возможное число ходов, неизменно одерживая победу в партии.

Позднее, в 1930-е годы, американский ученый Вэнивар Буш создал цифровой электрический компьютер и несколько машин для решения дифференциальных уравнений. Даже в первом электромеханическом компьютере Harvard Mark I, который был создан в период с 1939 по 1943 год американским инженером Говардом Хатауэем Эйкеном при поддержке IBM, 760000 зубчатых колес и 800 километров проводов были расположены по схеме, предложенной Бэббиджем.

Если бы аналитическая машина Бэббиджа была построена, в ней было бы 30 метров в длину, 10 метров в ширину и 4,5 метра в высоту. Сложение выполнялось бы за 3 секунды, умножение — от 2 до 4 минут, не считая времени, затраченного на ввод данных в арифметическое устройство — это заняло бы еще 2,5 секунды.

Чарльз Бэббидж также известен благодаря многим другим открытиям. Он взломал шифр Виженера (вариант шифра Цезаря), разработал приспособление, сбрасывающее посторонние предметы с путей перед локомотивом, а также сформулировал экономический «принцип Бэббиджа». Он также создал современную почтовую систему и был первым, кто указал, что ширина колец на спиле дерева зависит от погодных условий, что позволило изучить климат прошлых лет.

В области философии и богословия, которые он также не обошел стороной, ему не удалось достичь столь значимых успехов. Он был очень верующим человеком и в 1837 году опубликовал «Девятый трактат Бриджуотера» (Ninth Bridgewater Treatise), последовавший за восемью трактатами по богословию, издание которых было оплачено из наследства преподобного Фрэнсиса Генри, графа Бриджуотерского. Бэббидж пытался доказать существование Бога с позиций математики. Он писал, что Бог как высший законодатель создал законы или программы, согласно которым различные виды живых существ появлялись тогда, когда это было необходимо, и не вмешивался в земные дела напрямую. Он также доказывал возможность происхождения чудес с математической точки зрения, использовав методы теории вероятности. Его работы были написаны в то же время, что и труды Чарльза Дарвина (1809–1882).

Логика и Джордж Буль

В 1847 году была опубликована книга «Математический анализ логики» (Mathematical Analysis of Logic) Джорджа Буля, в которой была представлена булева алгебра — попытка применить методы алгебры к логике первого порядка. В настоящее время булева алгебра в общем виде используется при проектировании электрических схем, однако изначально открытия Буля были признаны только узкими специалистами. Лишь в XX веке была понята их важность и возможность применения в информатике.

Большая заслуга в этом принадлежит американскому математику и инженеру Клоду Шеннону (1916–2001), который считается создателем теории информации. Шеннон познакомился с работой Буля на занятиях по философии в Мичиганском университете, и в 1937 году защитил магистерскую диссертацию в Массачусетском технологическом институте (MIT), показав, что булеву алгебру можно использовать для оптимизации электрических цепей. В 1935 году независимо от Шеннона логик Виктор Шестаков (1907–1987) из Московского государственного университета также использовал булеву алгебру в этих же целях.

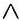Булева алгебра оказалась столь полезной в информатике потому, что она описывает идеальный сценарий с точки зрения двоичной логики. В ней используются только нули и единицы, основными операциями являются И, ИЛИ и НЕ, то есть конъюнкция (бинарная операция, обозначаемая ), дизъюнкция (бинарная операция, обозначаемая 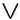) и отрицание (унарная операция, обозначаемая ¬). Эти логические операции определяются с помощью следующих таблиц истинности.

Другие привычные операции, например импликация (операция, схожая с конструкцией «если… то»), выражаются через три основные операции, представленные выше: (х — > у) = ¬ х 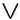 y, Кроме того, в виде комбинации этих операций можно представить любую другую логическую функцию. Так называемый закон де Моргана гласит, что существует всего две основные логические операции. Например, это могут быть дизъюнкция и отрицание, с помощью которых также можно выразить операцию конъюнкции.

* * *

ДЖОРДЖ БУЛЬ (1815–1864)

Британский математик и философ Джордж Буль создал алгебру, которая стала основой современной вычислительной техники. Именно поэтому он считается одним из основателей информатики. Его важнейшими математическими трудами являются Treatise on Differential Equations («Трактат о дифференциальных уравнениях»), опубликованный в 1859 году, и его продолжение Treatise on the Calculus of Finite Differences («Трактат о конечных разностях»), вышедший в 1860 году. Свою систему правил для математической записи и упрощения логических и философских задач, аргументы которых могут принимать только два значения (истина или ложь), он изложил в труде «Исследование законов мышления, на которых основываются математические теории логики и вероятностей» (An Investigation of the Laws of Thought, on Which are Founded the Mathematical Theories of Logic and Probabilities).

* * *

Аксиоматика булевой алгебры строится на основе свойств. Говоря неформальным языком, эти свойства являются необходимыми и достаточными для составления таблиц истинности логических операций.

Число π в XIX веке

В середине XVIII века, точнее в 1761 году, немецкий математик, физик, астроном и философ французского происхождения Иоганн Ламберт (1728–1777) показал, что число π и его квадрат π² являются иррациональными числами. Тем самым была доказана невозможность вычислить их «точное» значение. Лишь 120 лет спустя работы по вычислению значения π снова обрели важность. В 1882 году математик Фердинанд Линдеман (1852–1939) доказал, что число π является трансцендентным. Это означало, что задача о квадратуре круга нерешаема с помощью циркуля и линейки.

Некоторые задачи, касающиеся числа π, до сих пор остаются открытыми, в частности задача о нормальности π. Иррациональное число является нормальным, если вероятность появления числовых последовательностей равной длины в его записи одинакова. Например, все цифры от 0 до 9 фигурируют в записи нормального с одинаковой вероятностью, равной 1/10, все последовательности из двух цифр — с вероятностью 1/100 и так далее. Нормальность числа π все еще не доказана, однако считается, что π действительно является нормальным. Были подсчитаны частоты, с которыми в его записи появляются различные цифры. В конце XX века американский математик Дэвид Бэйли проанализировал первые 29360000 знаков π. Рассмотрев последовательности длиной до 6 цифр включительно, он не обнаружил никаких признаков неравномерности. Различия в частотах оказались минимальными и не имели статистической значимости. Приведем в качестве примера частоты, с которыми в записи π появляются цифры от 0 до 9.

* * *