Кантор столкнулся с проблемой подсчета бесконечности. Ранее потенциальная бесконечность определялась через возможность беспредельно добавлять к ряду или последовательности все новые и новые элементы, но Кантор предложил ввести понятие актуальной бесконечности, иными словами, начать использовать бесконечность как еще одну математическую сущность. Для этого следовало пересмотреть и полностью формализовать такое элементарное арифметическое действие, как простой подсчет совокупности объектов, что требовало решения двух задач: нужно было, во-первых, четко определить, что понимается под совокупностью объектов, и, во-вторых, дать математическое определение подсчету объектов совокупности.

Первая задача была решена с помощью теории множеств, которую на тот момент уже разработал Больцано. Кантор расширил и дополнил ее, что дало возможность вести речь об элементах множества как о совершенно абстрактных сущностях.

Многие историки науки считают теорию множеств Кантора одним из самых выдающихся творений человеческой мысли. Мы не будем вдаваться в детали этой теории, так как в нашем контексте будет достаточно нескольких интуитивно понятных определений, однако отметим, что понятие множества является одним из фундаментальных понятий математики, так как на него опираются все теоретические основы науки. Анри Пуанкаре (1854–1912) как-то сказал, что математик — это человек, дающий разным вещам одно наименование. Эта короткая и немного ироничная фраза отражает важную истину: конечная цель, к которой стремятся математики, — обобщение.

Замечание Пуанкаре в высшей степени применимо к теории множеств, поскольку слово «множество» может означать любое существующее понятие (а также многие несуществующие). Именно это обобщение позволило Кантору дать четкое определение актуальной бесконечности.

Первая трудность теории множеств состоит в самой дефиниции понятия «множество», так как его очень сложно определить, не используя само понятие «множество» или один из его синонимов — объединение, группа и т. д.

Одно из наиболее удачных определений, в котором не используются синонимы слова «множество» (по крайней мере, явным образом), принадлежит Бертрану Расселу: «Множество есть совокупность различных элементов, мыслимая как единое целое». Это интересная точка зрения, так как в ней понятие множества определяется как результат мыслительной деятельности, и это означает, что речь идет о фундаментальном понятии.

* * *

* * *

Как мы уже говорили, фундаментальным также является понятие подсчета элементов множества. При счете мы в действительности сравниваем элементы двух множеств. Например, если мы хотим узнать, сколько человек находится в помещении (то есть сколько элементов содержит множество людей, находящихся в помещении), мы берем за основу известное множество, образованное натуральными числами 1, 2, 3, …, и присваиваем каждому человеку в помещении порядковый номер без повторений. Закончив подсчет, мы смотрим, какое число мы присвоили последним. Если это число равно, например, 23, мы говорим, что в помещении находится 23 человека. В действительности мы сравнили два множества — множество людей и множество чисел {1, 2, 3, …, 22, 23}, установив так называемое взаимно однозначное соответствие. Взаимно однозначное соответствие можно установить между множествами разной природы, важно лишь, чтобы при этом соблюдались определенные правила. Например, если даны множество заглавных букв {А, F, H, P, V} и множество строчных букв {a, b, с, d, е}, то между ними можно установить следующее отношение: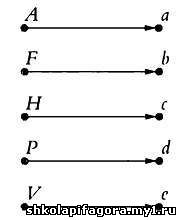

Каждому элементу первого множества должен соответствовать один и только один элемент второго множества, и наоборот. Это единственное правило, которому должны подчиняться биективные, то есть взаимно однозначные отображения.

На рисунке ниже мы также видим соответствия:

Однако они не удовлетворяют этому правилу.

Таким образом, Кантор определил простейшее понятие подсчета, а также ввел понятие кардинальности множества.

Если мы рассмотрим множества, между которыми можно установить биективное отображение, то увидим, что число элементов в этих множествах одинаково.

Но если одно множество состоит из четырех элементов, а другое — из трех, между ними нельзя установить биективное отображение: какой-либо элемент остается без пары или какому-либо элементу будет сопоставлено сразу несколько элементов.

Кантор определил эквивалентность множеств следующим образом: «Кардинальность двух множеств одинакова, если между ними можно установить биективное (взаимно однозначное) отображение». О множествах с одинаковой кардинальностью говорят, что они являются равномощными, то есть имеют одинаковое число элементов.

Таким образом, если дано произвольное множество, например коробка цветных карандашей, которое мы обозначим А, и можно установить взаимно однозначное соответствие между множеством A и множеством N = {1, 2, 3, 4, 5, 6}, то говорят, что кардинальность А и N одинакова:

|A| — |N| = 6.

Может показаться, что мы усложняем очевидное, но это впечатление обманчиво: новый логический аппарат позволил дать четкое определение бесконечному множеству.

Для этого сначала определим, что такое конечное множество. Непустое множество А (иными словами, содержащее как минимум один элемент) является конечным, если для некоторого числа n множество А имеет ту же кардинальность, что и множество {1, 2, 3, …, n}. Следовательно, n будет числом элементов множества A. В противном случае говорят, что множество А бесконечное.

Аналогично: множество А бесконечно, если существует собственное подмножество В множества А, имеющее ту же кардинальность, что и само А. В противном случае множество А является конечным.

На последнем определении стоит остановиться подробнее ввиду его чрезвычайной важности. Во-первых, следует пояснить, что понимается под собственным подмножеством. Это очень просто: если дано произвольное множество А, например {a, b, с, d}, его собственным подмножеством будет любое подмножество, которое можно составить из элементов А, при этом нельзя использовать их все. Примерами собственных подмножеств А будут:

{а} {а, Ь} {а, b, с} {а, с, d} {d} {b, с, d}.

В соответствии с вышесказанным кажется логичным, что между множеством и его собственным подмножеством нельзя установить взаимно однозначное соответствие: собственное подмножество всегда будет содержать меньше элементов, чем само множество.

Но существуют примеры, когда это не так. Рассмотрим 

n —> 2n

В соответствии с этим

1 —> 2

2 —> 4

3 —> 6

…

Иными словами, каждому натуральному числу соответствует четное число и, напротив, каждому четному числу соответствует натуральное число. Это означает, что кардинальность этих множеств одинакова, и утверждение «существует столько же натуральных чисел, сколько четных» вовсе не парадокс, хотя оно явно противоречит интуиции. Таким образом, альтернативное определение бесконечного множества звучит так: множество является бесконечным, если между этим множеством и какой-либо из его частей (каким-либо его собственным подмножеством) можно установить взаимно однозначное соответствие.

В этом случае парадокс, сформулированный Галилеем (см. главу 3), — это уже не парадокс, а констатация факта: множество натуральных чисел является бесконечным.

Путем аналогичных рассуждений можно доказать, что множество натуральных чисел