.Кантор также сформулировал очень важное понятие счетного множества. По определению, множество А называется счетным, если можно установить взаимно однозначное соответствие между А и подмножеством N . В основе этого определения лежит очень простая идея, которую мы часто используем в повседневной жизни. Когда
мы заявляем, что места в зале кинотеатра пронумерованы, мы говорим о
взаимно однозначном соответствии между подмножеством натуральных чисел и
множеством кресел и сопоставляем каждому креслу число. Мы
уже показали, что множество целых чисел является счетным. Далее Кантор
получил поистине удивительный результат: множество рациональных чисел Q
также является счетным. Он доказал, что существует столько же
рациональных чисел, сколько и натуральных. Чтобы установить соответствие
между натуральными и рациональными числами, Кантор использовал
настолько простую схему, что остается только удивляться, почему никто не
сделал этого раньше. Возможно, причина в том, что никто не считал это
возможным, так как это противоречит элементарной интуиции. 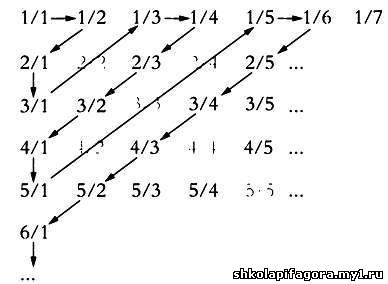 Схема,
придуманная Кантором, такова. Нужно построить таблицу рациональных
чисел (напомним, что речь идет о дробях) следующим образом: в первой
строке записываются дроби, числитель которых равен 1, во второй — дроби,
числитель которых равен 2, в третьей — 3 и т. д. Вычеркнем из каждой
строки повторяющиеся дроби. Например, 2/2 — это то же самое, что 1/1 или
3/3, 2/4 — то же, что и 1/2, и т. д. Построив таблицу, обойдем все
числа в порядке, указанном стрелками, начиная с 1/1. Мы обойдем все
рациональные числа ровно один раз. Таким образом, взаимно однозначное
соответствие между натуральными и рациональными числами устанавливается
следующим образом: 1 —> 1/1 2 —> 1/2 3 —> 2/1 4 —> 3/1 5 —> 1/3 … Самое
удивительное в том, что мы установили взаимно однозначное соответствие
между двумя множествами, одно из которых является дискретным (множество
натуральных чисел), а другое — плотным (множество рациональных чисел). Здесь
бесконечность начинает понемногу приподнимать завесу тайны над своими
удивительными загадками. Интуиция подсказывает, что счетными могут быть
только дискретные множества, и тот факт, что плотное множество Q
также является счетным, был поистине удивительным. Мы подсознательно
ассоциируем счетность с возможностью найти следующий элемент для
данного, что невозможно в плотном множестве. Если мы рассмотрим
предыдущую таблицу, то увидим, что 1/1 является первым числом, а
следующим будет 1/2. Однако множество дробных чисел является плотным,
поэтому между 1/1 и 1/2 находится бесконечное множество чисел. Так, нам
известно, что 1/4 находится между 1 и 1/2, а в нашем перечне это число
занимает шестое место. * * * МЫСЛИТЬ — ЭТО БОЛЬШЕ, ЧЕМ ГОВОРИТЬ Согласно
теории множеств Кантора, множество всех возможных слов, как
произнесенных, так и записанных на бумаге, является счетным. Если
учитывать, что множество знаков (букв, символов и т. д.) в языке
конечно, то очевидно, что на его основе можно сформировать счетное
множество. Другое дело — множество вещей, о которых мы можем подумать.
Оно, очевидно, не является счетным. Мы можем представить, например,
множество окружностей на плоскости, имеющее мощность континуум. Таким
образом, все, что мы можем сказать, поддается упорядочению, а все, о чем
мы можем подумать, не поддается или поддается лишь частично.
Следовательно, можно упорядочить лишь часть наших мыслей, а большинство
из них принадлежит к миру хаоса. Буквы алфавита образуют ограниченное и, следовательно, счетное множество. * * * По
этой причине с открытым Кантором понятием счетности оказалось тесно
связано понятие непрерывности. Неизбежно возник вопрос: если расширить
множество рациональных чисел иррациональными, будет ли полученное
множество счетным? Иными словами, можно ли говорить, что М — счетное множество? Нет,
это не так, и Кантор это доказал с помощью метода, схожего с тем,
который он использовал при доказательстве счетности множества Q ,
но намного более сложного. Также, используя метод доведения до абсурда,
он показал, что множество (0, 1) всех вещественных чисел, заключенных
между 0 и 1, не является счетным, следовательно, М
также не может быть счетным. Таким образом Кантор создал серьезный
прецедент, сыгравший определяющую роль в математике XX века. Достаточно
сказать, что этот прецедент стал частью доказательства знаменитой
теоремы Геделя о неполноте.
| 
