|
Пифагорейцам не были известны дроби в том виде, в котором мы их
используем сейчас. Вместо этого применялось эквивалентное понятие
отношения между целыми числами. Как вы уже увидели, с помощью таких
отношений пифагорейцы описали соотношения длин струн, способных
производить гармоничные звуки: 2:1, 3:2, 4:3, …
Пифагорейцы были твердо убеждены в том, что числа выражали
гармонию Вселенной, поэтому две величины всегда должны быть соизмеримы:
их отношение должно выражаться как отношение целых чисел. Понятие
соизмеримости напрямую связано с числами, которые мы называем
рациональными. Рациональное число — это число, представляемое
обыкновенной дробью, числителем которой является целое число, а
знаменателем — натуральное. На языке современной математики
пифагорейское понятие соизмеримости будет звучать так: две произвольные
величины А и В соизмеримы, если существует третья величина С и два целых числа р и q такие, что С укладывается в А р раз, а в В — q раз.
 Иными словами, можно, используя всего два целых числа, точно определить, во сколько раз А больше (или меньше) В.
Однако уже пифагорейцы, к своему неудовольствию, обнаружили, что
существуют несоизмеримые числа, отношение между которыми нельзя
представить с помощью целых чисел. В настоящее время такие числа
называют иррациональными. Самые известные иррациональные чисда — это π и √2. Корень из двух — это длина гипотенузы прямоугольного треугольника с катетами длиной 1, вычисленная по теореме Пифагора. * * *
ТРИ СРЕДНИЕ ВЕЛИЧИНЫ
Пифагор находился под влиянием своих знаний о средних величинах
(среднем арифметическом, среднем геометрическом и среднем гармоническом)
и о мистицизме натуральных чисел, особенно первых четырех, называемых
«тетракис».
Как видно на рисунке ниже,
3:4 — это среднее арифметическое 1 и 1/2:
2:3 — среднее гармоническое 1 и 1/2:
Пифагор экспериментально доказал, что струны с соотношением длин
1:2,2:3 (среднее гармоническое 1 и 1/2) и 3:4 (среднее арифметическое 1 и
1/2) издают приятные звуки. Как вы уже знаете, на основе этих
соотношений он создал свой музыкальный строй. Пифагор назвал эти
интервалы диапазон, диапент и диатессарон. Мы называем эти интервалы
октавой, квинтой и квартой соответственно. Но что случилось со средним
геометрическим? Пифагор отказался от него, так как оно было несоизмеримо
с остальными? Вовсе нет: среднее геометрическое точно соответствует
ноте фа-диез хроматического строя.
* * *
Как вы уже увидели, при настройке интервалов так, чтобы
соотношение частот равнялось 18/17, что предлагал Винченцо Галилей,
нельзя получить чистые октавы. Число 18/17 достаточно точное, но стоит
задаться вопросом: существует ли рациональное число, равное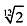 
— соотношению частот для интервалов равномерно темперированного строя?
Иначе говоря, существуют ли два целых положительных числа а и b такие, что
Их не существует. Следовательно, если соотношение частот звуков описывается отношением целых чисел а/Ь, то цепочка из 12 полутонов не будет равна «настоящей» октаве. Если бы такие числа существовали, то выполнялось бы равенство
и, как следствие, существовали бы два целых числа а’ = а6 и b’ = b6 такие, что (а’/Ь’)2 = 2. Следовательно, число √2 было бы рациональным, что невозможно.
Что сказали бы пифагорейцы, увидев, что задача о создании идеального музыкального строя решается с помощью иррациональных чисел?
| 
