Как создаются новые лекарства? Еще совсем недавно фармацевты готовили медикаменты вручную, а их единственными помощниками были бумага и карандаш.

Они создавали и оптимизировали химическую структуру лекарства и в специальных лабораториях синтезировали и испытывали все новые и новые их версии, чтобы подтвердить, действительно ли возросла эффективность таблеток. Этот метод проб и ошибок отчасти объясняет, почему стоимость разработки нового лекарства в среднем составляет 1 млрд долларов.

При создании нового средства, как правило, синтезируется новая молекула, взаимодействующая с неким белком и в конечном итоге нейтрализующая его действие.

В живых организмах белки участвуют в метаболическом каскаде — последовательности реакций. Следовательно, если молекула нейтрализует действие одного из белков, участвующих в интересующей нас последовательности реакций, каскад будет нарушен, а молекула станет хорошим лекарством.

В этом упрощенном сценарии лекарство препятствует взаимодействию белка-мишени с белком с и нарушает метаболический каскад.

Чтобы нейтрализовать один из этих белков, необходимо, чтобы молекулы лекарства соединялись с ним определенным образом. Следовательно, большая часть усилий при создании нового медикамента направлена на то, чтобы новая молекула присоединялась к активному центру нужного белка — мишени.

Чтобы определить, действительно ли молекула лекарства соединяется с молекулой белка, необходимо измерить энергию их взаимодействия. Энергия взаимодействия между молекулой-кандидатом и белком-мишенью — это энергия, которую необходимо приложить для сохранения связи в системе. К примеру, если мы хотим, чтобы магнит держался на двери холодильника, нам не нужно постоянно прикладывать какую-то силу. Достаточно мощный магнит, только поднеси его к дверце, сам по себе притянется к ней с определенной силой. В этом случае говорят: для того чтобы магнит оставался прикрепленным к дверце холодильника, требуется приложить отрицательную энергию.

Разумеется, молекула лекарства, которая не образует связи с молекулой белка-мишени, не окажет лечебного воздействия: такая молекула будет свободно перемещаться по кровеносной системе или тканям, никак не решая задачу нейтрализации белка. А хорошим лекарством будет соединение, для которого энергия взаимодействия будет отрицательной и минимально возможной, — это говорит нам о том, насколько сильно притягиваются молекулы лекарства и белка. Следовательно, основной параметр, значение которого следует оптимизировать при разработке нового лекарства, это энергия взаимодействия.

Подобные задачи, решение которых заключается в определении ряда оптимальных параметров (например, какой шахматной фигурой нужно сделать ход, чтобы выиграть партию, или какими должны быть положение и размеры балок моста, чтобы снизить стоимость строительства и повысить прочность конструкции), объединяются в категорию задач поиска. При этом часто требуется найти параметры, обеспечивающие максимальное значение некой математической функции. В этом случае поиск называется оптимизацией.

Чаще других для решения задач поиска применяется метод эволюционных вычислений. При этом происходит оптимизация значений функций различной сложности, подобно тому как живые организмы эволюционируют, чтобы повысить выживаемость в окружающей среде.

Идею эволюционных вычислений предложил исследователь Джон Холланд в 1975 году в своей книге «Адаптация в естественных и искусственных системах» (Adaptation in Natural and Artificial Systems). Позднее западные ученые обнаружили, что немецкие инженеры уже использовали подобные стратегии для оптимизации формы сопл первых реактивных двигателей самолетов во время Второй мировой войны. Эволюционные вычисления охватывают широкий спектр методов и алгоритмов, целиком основанных на законах естественной эволюции, предложенных Дарвином. Согласно его законам, лучше всего к жизни в определенной среде подготовлены особи, которые демонстрируют более высокую выживаемость и, как следствие, оставляют больше потомства.

В этой аналогии с законами естественной эволюции особям соответствуют возможные решения задачи. Эволюционные алгоритмы сначала оценивают пригодность каждой «особи», а затем определяют, каким будет их «потомство» — второе поколение решений. В ходе итеративного процесса особи из последующих поколений оцениваются, отбираются и скрещиваются между собой, формируя новые поколения особей. Этот процесс заканчивается после выполнения установленных для задачи критериев останова. 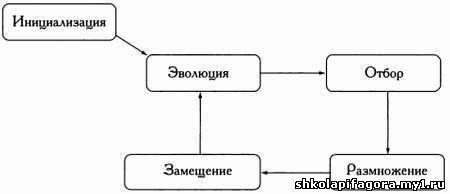Таким образом, любой эволюционный алгоритм состоит из пяти основных этапов: инициализации, оценки, отбора, размножения и замещения, как показано на следующей схеме.