В этой главе мы совершим краткий экскурс в историю
метра. Сначала мы расскажем, как производились измерения в XVIII веке, с
какими трудностями было сопряжено использование множества единиц
измерения, а также в каких исторических обстоятельствах появилась
универсальная система мер. Мы укажем, какими свойствами должна была
обладать новая единица длины, перечислим высказанные предложения и
объясним, почему в конечном итоге было принято решение определить новую
единицу длины по результатам измерений дуги меридиана. Вы узнаете о
математических методах (триангуляции) и измерительных инструментах
(повторительном круге Борда), которые использовались при реализации
этого проекта, а также о его руководителях (Жан-Батист-Жозефе Деламбре и
Пьере Мешене). Кроме того, мы расскажем о приключениях и злоключениях,
которые пришлось пережить участникам геодезических экспедиций. В конце
главы мы опишем, как проходило распространение метрической системы, а
также упомянем некоторые конфликты, связанные с ней.
Потребность в универсальной мере длины
Мы привыкли, что расстояния на указателях
автомобильных дорог приводятся в километрах, растительное масло мы
отмеряем в литрах, а картофель — в килограммах, но в XVIII веке этих
единиц измерения не существовало. Одни и те же величины измерялись
разными единицами в зависимости от страны, региона и даже населенного
пункта, поэтому при въезде в некоторые города указывались принятые в них
официальные единицы измерения.
Приведем несколько примеров единиц длины: вара в
Валенсии равнялась примерно 0,906 м, в Теруэле — 0,768 м. Купив
несколько вар ткани в Валенсии и продав ее по той же цене в Теруэле,
можно было получить прибыль в 18 %. Испанская лига равнялась 5572 м,
французская — 3898 м (между прочим, лига упоминается в романе «Дон
Кихот» 64 раза). Футы также заметно отличались: испанский равнялся
0,278 м, французский — 0,324 м. Фут — особая единица длины, так как он
имеет отношение к испанской железной дороге: согласно королевскому указу
от 1844 года, ширина колеи железной дороги равняется 6 испанским футам
(6 x 0,278 = 1,67 м). Ширина колеи современных железных дорог в Европе,
установленная по образцу английской колеи, равняется 4 английским футам и
8,5 дюймам (1,43 м). Фунт также существовал во множестве вариантов: до
учреждения метрической системы в Европе эта единица измерения
существовала в 391 варианте.
* * *
КАК ЖЕ МНОГО ЭТИХ ФУТОВ!
Чтобы продемонстрировать, насколько могли отличаться
одни и те же единицы измерения, приведем пример антропоморфной меры —
фута, который использовался во многих странах, и его соотношение с
метром.
Испанский фут: 0,278 м
Французский фут: 0,324 м
Рейнский фут: 0,314 м
Римский фут: 0,297 м
Амстердамский фут: 0,283 м
Швейцарский фут: 0,300 м
Английский фут: 0,304 м
Русский фут: 0,305 м
Египетский фут: 0,225 м
Австрийский фут: 0,316 м
* * *
Обилие единиц измерения и различия между ними в
разных регионах затрудняли торговлю и вызывали огромные проблемы при
перевозке грузов. Их унификация стала одной из целей Великой французской
революции. 9 февраля 1790 года Клод-Антуан Приёр-Дювернуа (1763–1832)
по прозвищу Приёр из Кот-д’Ор, военный инженер, отвечавший за
реквизирование оружия и боеприпасов на нужды революции, подал по этому
поводу петицию в Национальное собрание Франции.
Проект по определению универсальных единиц измерения
способствовал не только социальному прогрессу — научное сообщество также
видело необходимость определения универсальных мер, и Французская
академия наук сыграла в реализации проекта немалую роль. Единицы
измерения должны были использоваться для измерения различных величин,
которые с точки зрения физики определялись как общие характеристики
различных объектов и веществ, например вина и масла. Если требовалось
измерить количество вина и масла, то не имело смысла использовать две
разные единицы измерения, так как оба этих вещества являются жидкостями —
достаточно одной, общей единицы. Спустя несколько лет была введена
такая единица измерения — литр.
Одна из основных физических величин — это длина,
которая является общей характеристикой для множества объектов и
позволяет определить их размеры. Существовало множество мер длины, и
казалось логичным начать с определения общей единицы измерения длины.
Кроме того, требовались точные инструменты — как для измерения эталона
длины, так и для изготовления необходимого числа его копий. Для
реализации проекта были все условия: совершенные ранее открытия
позволяли изготовить очень точные измерительные инструменты.
При определении требований к новым универсальным
единицам измерения решающую роль сыграли идеи равенства, провозглашенные
французской революцией. Этих требований было три: во-первых, новые
единицы измерения были обязательными к применению во всех странах,
во-вторых, они должны были быть неизменными, в-третьих, они не должны
были быть антропоморфными.
Выбор меридиана
Какими свойствами должна была обладать новая мера
длины? Какие предложения звучали и как было принято окончательное
решение? Наконец, почему было решено измерить длину дуги меридиана и
какую именно? Ответы на эти вопросы были получены по результатам трех
экспедиций, организованных с целью установления метра как универсальной
единицы измерения расстояния.
Свойства новой меры длины
Согласно постановлению Французской академии наук,
требовалось найти меру длины, которая бы определялась на основе некоего
явления природы, так как природа считалась неизменной и принадлежащей
всему человечеству. Таким образом удалось бы обеспечить стабильность
новой меры и ее неизменность с течением времени.
Но какое явление природы могло стать основой для
такой единицы измерения при соблюдении вышеуказанных условий? Было
рассмотрено три варианта: первый — длина маятника, второй — длина дуги
экватора, третий — длина дуги меридиана.
Какие размеры должна была иметь новая мера длины,
чтобы ее было удобно использовать в обычной жизни? В качестве отправной
точки была выбрана мера, равная половине туаза. Таким образом, три
приведенных выше варианта уже можно было рассмотреть подробнее. Этим
занялась комиссия Французской академии наук по просьбе Национального
собрания.
Три предложения
8 мая 1790 года, спустя три месяца после того, как
Приёр из Кот-д’Ор предложил определить универсальную меру длины,
Национальное собрание на своем специальном заседании обсудило различные
варианты. Прозвучало два важных доклада, в которых обосновывалась
необходимость проведения метрической реформы и определения новой меры
длины на основе длины маятника. Шарль Морис де Талейран, председатель
собрания и епископ Отёна, предложил считать эталоном длины маятник,
отсчитывавший секунды на широте 45°. Во втором докладе, прочитанном
самим Приёром из Кот-д’Ор, указывалось, что новая система мер должна
быть десятичной. Приёр разделил маятник на три равные части длиной в
один фут и описал следующую десятичную систему: фут равнялся 10 дюймам,
дюйм — 10 линиям.
Заслушав все доклады, собрание поручило Академии наук
изучить высказанные предложения и определить, как следует провести
реформу системы мер. Академия, в свою очередь, организовала комиссию,
куда вошли самые известные ученые того времени: Пьер-Симон Лаплас, Жозеф
Луи Лагранж, Жан-Шарль де Борда, Гаспар Монж и Никола де Кондорсе. 19
марта 1791 года комиссия опубликовала доклад, где были представлены три
варианта меры длины, пригодной во все времена и для всех народов:
— длина маятника, половина периода колебаний которого равна одной секунде на 45° широты;
— четвертая часть экватора;
— четвертая часть меридиана.
* * *
ЕДИНИЦЫ ИЗМЕРЕНИЯ В ДЕСЯТИЧНОЙ И ДРУГИХ СИСТЕМАХ СЧИСЛЕНИЯ
Эффективность десятичной системы счисления по
сравнению с другими четко проявляется при выполнении расчетов. Так,
чтобы найти сумму двух длин, к примеру 3 м + 7 см = 3,07 м или 307 см, в
десятичной системе, достаточно перевести одну единицу измерения в
другую, умножив или разделив ее на 10 нужное число раз (отсюда и
название). Сумму 1 ч 35 мин + 42 мин, напротив, нельзя записать в виде
1 ч 77 мин — правильным ответом будет 2 ч 17 мин, поскольку соотношение
между часами и минутами равно не 10 в какой-либо степени, а 60.
В системах счисления, отличных от десятичной, также
сложнее выполнять действия с дробями. Рассмотрим 1/4 + 1/2 = 3/4. В
десятичной системе
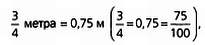
или 75 см, а 3/4 часа = 45 мин. что уже нельзя
выразить ни как 75 мин, ни как 7,5, ни какой-либо еще дробью со
знаменателем 10, 100 и так далее, так как в этом случае 3/4 = 45/60.
Хотя соотношения между часами, минутами и секундами
описываются не десятичной, а шестидесятеричной системой счисления,
использовать ее сравнительно просто, поэтому она и сохранилась до наших
дней. Пересчет других единиц измерения в иных системах счисления
былнамного сложнее, так что с введением метра эти единицы измерения ушли
в прошлое.
* * *
Окончательное решение
Французская академия наук поддержала десятичную
систему, предложенную Приёром, и склонилась к тому, чтобы из трех
предложенных вариантов выбрать в качестве новой единицы измерения длину
меридиана. После публикации доклада Академии наук окончательное решение
оставалось за Национальным собранием.
26 марта 1791 года Национальное собрание утвердило
решение Академии наук и выбрало третий вариант из предложенных. Собрание
постановило: «Единицей измерения длины станет четвертая часть земного
меридиана, а общеупотребительной мерой длины — десятимиллионная ее
часть». На том же заседании было утверждено название новой единицы
измерения — «метр» (от древнегреческого 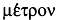 — «мера»). — «мера»).
Почему Академия наук определила метр на основе длины земного меридиана?
К тому времени уже было получено несколько достаточно
точных оценок его длины, однако требовалось реализовать намного более
масштабный проект, который позволил бы добиться высокой точности
измерений, необходимой для определения новой меры. Зачем нужно было
начинать намного более дорогостоящий проект, чем тот, в котором метр
определялся на основе маятника? Решение комиссии вызвало возмущение
некоторых государственных деятелей, в числе которых был и Жан-Поль
Марат. Академия наук к тому моменту неоднократно отвергла его научные
труды, большинство из которых было посвящено физике.
Комиссия отказалась от измерения экватора, так как
производить измерения в малоизвестных областях было затруднительно.
Ученые еще помнили, с какими трудностями столкнулась экспедиция в
вице-королевство Перу. И все же: почему не маятник — сравнительно
удобный и дешевый вариант? Комиссия указала, что единица измерения длины
не может зависеть от единицы измерения времени и силы тяготения.
Является ли время более «базовой» физической величиной, чем длина? Со
временем эти противоречия оказались забыты: в последующих определениях
метра, которые точнее соответствовали новым требованиям науки и техники,
эти две величины оказались связаны воедино, о чем мы еще расскажем.
По мнению некоторых историков, причина заключалась в
том, что один из членов комиссии, Борда, создал очень точный инструмент
для измерения углов. Измерение меридиана в конечном счете доказало бы
эффективность этого инструмента, и его можно было бы использовать для
топографических и астрономических расчетов.
Выбор дуги меридиана
Так как измерить длину четверти меридиана от
Северного полюса до экватора невозможно, была предпринята попытка
измерить максимально возможную дугу меридиана по суше и экстраполировать
результаты. Чтобы компенсировать воздействие рельефа и неидеальной
формы Земли, следовало выбрать дугу меридиана вблизи 45-й параллели,
такую, что ее концы находились бы на уровне моря, а в середине не было
бы высоких гор. Таким образом, требовалось обойти два крупнейших горных
хребта Европы — Альпы и Карпаты.
На иллюстрации изображена дуга меридиана, на основе которой был определен метр. Буквой Е обозначен экватор, В — Барселона, D — Дюнкерк.
Были рассмотрены три варианта: Амстердам — Марсель, Шербург — Мурсия и Дюнкерк — Барселона.
В итоге был выбран третий вариант, так как ранее, в
1739 году, на этом меридиане уже были проведены частичные измерения —
так, было измерено расстояние от Дюнкерка до Перпиньяна. Возможно, на
решение повлияло и то, что на этом меридиане находился Париж, и именно
по этой причине от участия в проекте в 1791 году отказались англичане,
которые ранее были готовы сотрудничать.
В апреле 1791 года комиссия Французской академии наук
поручила реализацию проекта Жан-Батист-Жозефу Деламбру, Жану Доминику
Кассини, Адриен-Мари Лежандру и Пьеру Мешену. Преданный королю Кассини
отказался сотрудничать с революционным правительством, заключившим под
стражу короля Людовика XVI. 15 февраля 1792 года Деламбр был единогласно
избран членом Академии наук. В мае 1792 года, после того как Кассини
окончательно отказался участвовать в проекте, Деламбру было поручено
возглавить экспедицию на север, из Родеза в Дюнкерк, Мешену — экспедицию
на юг, из Родеза в Барселону.
В январе 1806 года, уже после смерти Мешена, Деламбр
закончил работу над трехтомным трудом, где были изложены все полученные
им данные, условия наблюдений и расчеты, выполненные в ходе
триангуляции. Труд носил название «Основы метрической десятичной
системы, или Измерение дуги меридиана, заключенной между параллелями
Дюнкерка и Барселоны. Выполнено в 1792 и следующих годах Мешеном и
Деламбром».
Обложка книги Мешена и Деламбра.
|

