Геодезические линии указывают кратчайшее расстояние между соседними точками, однако в общем случае это не так. Например, часть меридиана, соединяющего Лондон и город Гао в Мали и проходящего через Северный полюс, Атлантический океан и Южный полюс, — это геодезическая линия, но она не соответствует кратчайшему пути из Лондона в Гао. Однако эта геодезическая линия соответствует кратчайшему пути между близлежащими точками, например между Гао и городом Аккра в Гане или между Лондоном и Северным полюсом.

Как всем хорошо известно, геодезическими линиями плоскости являются прямые. Тем не менее минимальное расстояние между точками на сфере указывают большие круги — кривые, получаемые сечением сферы плоскостями, проходящими через ее центр. Примерами больших кругов сферы являются меридианы. Единственная параллель, которая является большим кругом, — это экватор.

На иллюстрации показаны большие круги Земли.

Проведем эксперимент. Допустим, что мы хотим провести прямую, проходящую через две точки плоской поверхности. Для этого мы можем соединить эти точки простой веревкой и сильно натянуть ее. Веревка примет форму прямой, соединяющей две точки. Теперь рассмотрим земной шар. Чтобы определить кратчайший путь между двумя точками земного шара, например между Барселоной и Аделаидой, соединим указанные точки веревкой и натянем ее. Мы получим кривую наименьшей длины, соединяющую два указанных города (то есть геодезическую линию), которая будет частью большого круга, проходящего через эти города, как показано на иллюстрации.

Натянутая веревка соответствует кратчайшему пути между двумя точками.

На интуитивном уровне можно сформулировать следующее доказательство. Допустим, даны две точки на сфере, и мы хотим найти кривую, которая определяет кратчайший путь между ними. Кажется логичным предположить, что мы можем ограничиться рассмотрением окружностей сферы, которые проходят через эти точки и образуются сечением сферы плоскостями, проходящими через две данные точки. Кроме того, в силу свойств симметрии, четко видно, что дуга окружности, полученной сечением сферы плоскостью, проходящей через центр сферы, соответствует кратчайшему пути между точками, что показано на предыдущем рисунке. В итоге большие круги являются геодезическими линиями сферы, или кривыми, указывающими наименьшее расстояние.

Дуга большого круга, заключенная между между двумя точками, имеет наименьшую длину среди всех дуг окружностей, соединяющих данные точки.

* * *

ГЕОДЕЗИЧЕСКИЕ КУПОЛА

Одно из самых впечатляющих сооружений сферической формы, созданных в XX веке, — это геодезические купола Ричарда Бакминстера Фуллера (1895–1983). Мы могли бы многое сказать об этом гениальном изобретателе, архитекторе, инженере, математике, поэте и космологе, провидце, который опередил свое время и смог поставить науку и технику на службу обществу. Величайшим его творением, несомненно, являются геодезические купола.

Американский павильон на Всемирной выставке 1967 года в Монреале, построенный по проекту Ричарда Бакминстера Фуллера. Позднее в павильоне разместился музей воды и окружающей среды

_{(фотография: Филипп Хайнсторфер).}

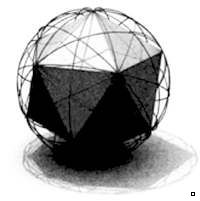
Геодезический купол — это сферическая структура, образованная сеткой больших кругов (геодезических линий). Треугольники, из которых состоит сетка, придают структуре жесткость. Для построения классического геодезического купола рассматривается икосаэдр, вписанный в сферу, как показано на иллюстрации. Затем каждая грань икосаэдра делится на треугольники, которые проецируются на сферу, образуя сетку геодезических линий.

Преимущества геодезического купола следующие.

1. Он покрывает обширное пространство и не требует поддерживающих конструкций в середине.

2. Для геодезического купола характерно оптимальное соотношение объема к площади поверхности, иными словами, он покрывает пространство максимального объема при наименьшей площади поверхности.

3. Пространство внутри купола нетрудно обогревать, так как потери тепла зависят от соотношения между объемом и площадью поверхности, которое является оптимальным.

4. Геодезические купола благодаря своей структуре и распределению нагрузки обладают высокой жесткостью.

5. Геодезические купола имеют малый вес и просты в сборке.

* * *