Лунные затмения предоставляют еще одно доказательство, пусть и не столь очевидное: они наблюдаются во всех частях Земли в один и тот же день, но в разное время. Чем дальше на восток находится наблюдатель, тем позже он увидит затмение. Так, максимальная фаза полного лунного затмения, произошедшего ночью с 20 на 21 февраля 2008 года, наблюдалась в 3 часа 26 минут по мировому времени (то есть по времени Гринвичского меридиана). Следовательно, полное лунное затмение в Испании, Франции, Алжире и Ливии наблюдалось 21 февраля в 4:26, в Англии, Мавритании и Сенегале — в 3:26, в Гренландии, на Атлантическом побережье Бразилии и в Аргентине — в 0:26, на Атлантическом побережье США, в Колумбии и Эквадоре — в 22:46 днем раньше, а в Мексике и центральной части США — в 21:26. Если бы Земля была плоской, лунные затмения наблюдались бы во всех ее частях в одно и то же время, ведь в этом случае время во всех ее частях было бы одинаковым. Это связано с тем, что время на Земле определяется в зависимости от положения солнца на небе. Полдень, то есть период, когда Солнце находится выше всего над горизонтом, в разных частях Земли наступает в разное время, так как Земля круглая, но если бы наша планета была плоской, полдень везде наступал бы одновременно.

На небе можно увидеть еще одно, очень убедительное доказательство: когда путешественник движется на север, звезды и созвездия смещаются на юг и постепенно скрываются за горизонтом. При этом на севере постепенно появляются другие звезды, которые путешественник никогда не смог бы увидеть в начальной точке своего вояжа. Так, если мы находимся в Южном полушарии, Полярная звезда будет нам не видна. Но когда мы начнем двигаться на север и пересечем экватор, она появится над горизонтом и постепенно будет подниматься все выше и выше. Когда мы достигнем Северного полюса, Полярная звезда окажется точно у нас над головой.

В плоском мире этого бы не произошло — во всех его уголках на небе были бы видны одни и те же созвездия.

Путешественник, который находится в Южном полушарии, не сможет увидеть Полярную звезду (а). Если он начнет двигаться на север, то в момент пересечения экватора (b). Полярная звезда взойдет над горизонтом. Если путешественник продолжит двигаться на север, то увидит, как Полярная звезда поднимается все выше и выше. Так, над Северным тропиком, широта которого равна 23,5°, Полярная звезда расположена под углом 23,5° к горизонту (с). На Северном полюсе путешественник увидит Полярную звезду точно над головой (d).

Если мы опустим взгляд и сфокусируем его на горизонте, то также увидим доказательства того, что Земля круглая (лучше всего при этом находиться на побережье или на корабле в открытом море). Мы увидим, что линия горизонта искривляется к краям — в плоском мире она не была бы так искривлена.

Но вот вам и самое убедительное и неоспоримое доказательство того, что Земля круглая. Допустим, что мы стоим на пляже и смотрим, как парусник движется от нас в сторону горизонта. Если бы Земля была плоской, парус становился бы все меньше и меньше, пока не стал бы совершенно неразличимым. Но в действительности так не происходит: когда корабль уплывает вдаль, сначала из виду пропадает его корпус, затем — палуба, паруса и, наконец, вершина самой высокой мачты с маленьким флагом, развевающимся на ветру. Причина этому — кривизна земного шара. Мы наблюдаем подобную картину, когда смотрим, как путник скрывается за холмом: сначала из вида пропадают его ноги, затем — туловище и, наконец, голова. Более того, именно благодаря этому эффекту горизонт выглядит как тонкая линия между морем и небом — если бы Земля была плоской, зона между морем и небом была бы нечеткой, и различить линию горизонта было бы нельзя.

* * *

НА КАКОМ РАССТОЯНИИ НАХОДИТСЯ ГОРИЗОНТ?

Когда мы перестаем видеть флаг на вершине мачты корабля, уходящего в море? Ответить на этот и другие подобные вопросы поможет знаменитая теорема Пифагора: «В прямоугольном треугольнике с катетами а и b и гипотенузой с выполняется равенство с² = а² + Ь²».

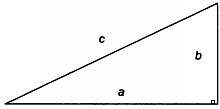
Сначала узнаем, на каком расстоянии от нас находится горизонт. Для этого предположим, что глаза наблюдателя, который смотрит на линию, разделяющую небо и море, находятся на высоте h = 1,70 м. Так как свет распространяется прямолинейно, то линия зрения, обращенная к горизонту, будет касательной к Земле. Учитывая, что, согласно простой теореме геометрии, «касательная к окружности перпендикулярна ее радиусу, проведенному в точку касания» (см. рис. на следующей странице), имеем прямоугольный треугольник, катетами которого будут линия зрения, направленная к горизонту (обозначим длину этого катета через d), и радиус Земли R (будем рассматривать радиус на экваторе, равный 6378137 м). Гипотенузой треугольника будет отрезок, соединяющий глаза наблюдателя с центром Земли. Длина гипотенузы равна R + h. По теореме Пифагора получим, что расстояние до горизонта равно почти 5 км:

Прямоугольный треугольник, катетами которого являются линия зрения, направленная к горизонту (длина этого катета равна d), и радиус Земли R, а гипотенузой — отрезок, соединяющий глаза наблюдателя с центром Земли. Длина этого отрезка равна R + h.