Карта мира в проекции Меркатора, несомненно, знакома многим из нас (по крайней мере, людям определенного возраста) лучше всех остальных карт. Можно сказать, что на протяжении почти четырех веков это название было нарицательным. В эпоху далеких путешествий и великих географических открытий, в XVI веке, мореплавателям и торговцам требовалась карта, которую можно было бы использовать для навигации. Такую карту создал фламандский ученый и картограф Герард Меркатор.

Созданная им проекция остается самой удобной и популярной до сих пор, недаром она легла в основу системы UTM (от англ. Universal Transverse Mercator — универсальная поперечная проекция Меркатора). Эту систему используют почти все международные агентства при составлении карт большого масштаба, то есть карт участков небольшой протяженности.

Определение и картографические свойства

Средневековые карты, не имевшие научной основы и составленные без использования математических проекций, были абсолютно бесполезны в навигации и не могли применяться для каких-либо измерений. Их использование нередко вело к тому, что корабли очень сильно отклонялись от курса и даже заплывали на совершенно неизвестные территории.

* * *

ГЕРАРД МЕРКАТОР (1512–1594)

Герард Меркатор был выдающимся человеком. Он занимался как практическими дисциплинами (его можно назвать картографом, географом, каллиграфом, гравером, изготовителем измерительных инструментов и редактором), так и теоретическими науками (Меркатор проявлял интерес к математике, астрономии, космографии, изучению земного магнетизма, истории, философии и богословию). В числе разработанных им карт выделяются карта Палестины 1537 года, очевидно, созданная по причинам религиозного характера, его первая карта мира, выполненная в проекции в форме двойного сердца (автором этой проекции был Оронций Финеус), карта Европы 1554 года, выполненная в проекции Вернера, карта Меркатора 1569 года, а также глобус, датируемый 1541 годом, — самый подробный глобус того времени. Последним проектом Меркатора стала работа над картой мира, состоящей из отдельных карт разных регионов. Меркатор опубликовал первую часть своего атласа (он первым использовал термин «атлас» для обозначения собрания карт «…в честь титана Атласа, царя Мавритании, большого философа, математика и астронома») в 1585 году. В сборник вошла 51 карта. Основное внимание уделялось картам Германии, Франции и Нидерландов. В следующий том, изданный в 1589 году, Меркатор добавил 23 карты Италии и Греции. Его сын Румольд опубликовал «Атлас Меркатора» в 1595 году, добавив в него еще 28 карт различных частей Европы. В атласе Меркатора использовались самые разные картографические проекции: конические, стереографическая, проекция Сансона — Флемстида, проекции Вернера, Меркатора и многие другие.

Портрет Герарда Меркатора, выполненный в 1574 году немецким художником Франсом Хогенбергом (1535–1590).

* * *

Первую попытку составить карты, которые можно было бы использовать в навигации, предприняли сами мореплаватели. Созданные ими карты, которые назывались портуланы, были основаны на заметках, сделанных во время путешествий, на данных астрономических наблюдений и на результатах измерений углов и румбов. При их создании использовались циркуль, транспортир, линейка и компас. Однако в портуланах не учитывались геометрические особенности сферы, то есть ее форма и кривизна, и при их составлении не применялась какая-либо картографическая проекция.

Попытки решить проблему составления навигационных карт с научной точки зрения предприняли Меркатор, Абрахам Ортелий и другие картографы того времени. Целью Герарда Меркатора было составить карту мира, пригодную для использования в навигации. Для этого карта должна была сохранять румбы (иными словами, используемая в ней проекция должна была быть конформной), а локсодромы — линии румба — должны были изображаться прямыми.

Португальский астроном и математик Педру Нуниш (1502–1578) описал и подробно изучил локсодромы (на поверхности Земли они имеют форму спиралей, закручивающихся к полюсам) в своем «Трактате о навигации» (1537). В этой книге Нуниш опроверг распространенное убеждение, согласно которому при сохранении неизменного румба судно двигалось вдоль дуги большого круга, то есть вдоль кривой минимальной длины. При прокладке курса между двумя точками Земли мореплаватели пытались следовать кратчайшему пути — ортодроме. Однако для этого требовалось постоянно изменять румб, из-за чего было нетрудно сбиться с курса. Вдоль локсодромы двигаться было удобнее — достаточно выдерживать постоянный румб, однако путь при этом получался длиннее. Уже в 1541 году Меркатор изобразил на созданном им глобусе множество локсодром.

Для построения навигационной карты требовалось решить геометрическую задачу: найти конформную проекцию, в которой локсодромы изображались бы прямыми на плоскости. Меридианы и параллели на карте должны были изображаться перпендикулярными прямыми. При подробном анализе проекции Ламберта, описанном в главе 5, мы выяснили, что равновеликая цилиндрическая проекция Ламберта не является конформной, так как вносимые ею искажения вдоль меридианов, равные cosφ, не равны искажениям в направлении параллелей, 1/cosφ = secφ, где φ — широта рассматриваемой точки. Необходимо было изменить карту так, чтобы искажения вдоль меридианов и параллелей совпадали. В частности, карту в проекции Ламберта нужно «растянуть» в направлении «север — юг». Карта станет не сжатой (искажение вдоль меридианов равно cosφ, а вытянутой (новое искажение будет равно 1/cosφ = secφ). В этом заключается основная идея построения нужной карты. Если мы выразим это искажение математически, получим выражение, описывающее искомую проекцию — проекцию Меркатора:

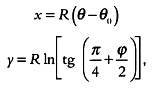
где θ — долгота (θ₀ — долгота центрального меридиана карты), φ — широта, а для сферической модели Земли R = 1.

Современная карта, выполненная в проекции Меркатора.

Именно это и сделал Меркатор при создании карты «Новое и улучшенное описание мира с исправлениями для использования в навигации» (Nova et aucta or bis terrae descriptio ad usum navigatum emendate accommodata) 1569 года: он построил сетку перпендикулярных друг другу меридианов и параллелей, а затем раздвинул параллели, чтобы компенсировать искажения вдоль меридианов. В результате искажения вдоль меридианов и параллелей на карте Меркатора оказались одинаковыми.

* * *

ПОРТУЛАНЫ

Карты мира, созданные в позднем Средневековье, были совершенно бесполезны для навигаторов. Мореплаватели полагались на собственные заметки, где описывались морские пути между портами, проложенные по результатам измерений, астрономических наблюдений и рекогносцировки побережий. После изобретения в XII веке компаса эти заметки стали более точными, начали появляться штурманские книги, в которых приводилась подробная информация о расстояниях и румбах. В какой-то момент на основе этих заметок начали создаваться карты побережий с информацией для мореплавателей — так называемые портуланы, которые стали первыми навигационными картами. На портуланах подробно описывались побережья и самым тщательным образом изображались порты, элементы рельефа и все, что представляло опасность для мореплавателей. Географические названия записывались перпендикулярно линии побережья, внутренние территории, как правило, оставались пустыми. На портуланах также изображались компасы и розы ветров, в которых сходились многочисленные линии румбов, внешне напоминавшие паутину, а также указывался масштаб карты. Мореплаватель с помощью линейки проводил прямую, соединявшую порт отплытия и порт назначения, после чего посредством параллельного переноса построенной прямой до ближайшей розы ветров определял румб, которым нужно было следовать. Хотя эти карты, в особенности карты средиземноморского побережья, были достаточно точными, картографическая информация в них была, очевидно, приближенной. На портуланах не учитывалась кривизна Земли, а при их построении не применялась какая-либо картографическая проекция.

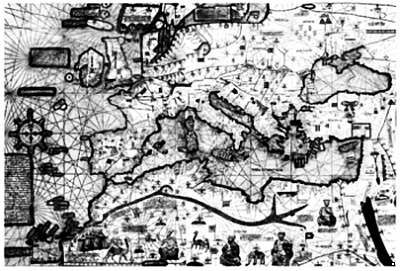Карта Европы и Средиземного моря из «Каталанского атласа» 1375 года. На иллюстрации представлена копия, выполненная в XIX веке.

* * *

Оригинальная карта Меркатора 1569 года.

В статье Джерома Сакса «Любопытная смесь карт, дат и имен» (A Curious Mixture of Maps, Dates, and Names, 1987) отмечается, что хотя в математическом уравнении проекции Меркатора используется логарифм, Джон Непер опубликовал свой труд о логарифмах лишь в начале XVII века. Кроме того, чтобы вывести уравнения проекции Меркатора, требовалось использовать методы математического анализа и дифференциальной геометрии, однако Ньютон и Лейбниц родились спустя 50 лет после смерти Меркатора, а Гаусс создал дифференциальную геометрию лишь в начале XIX века. Как же Меркатор составил свою карту в 1569 году? Видимо, не располагая методами, которые появились в математике позднее, он обладал обширными знаниями в области картографии и, как следствие, развитой интуицией.

Методы Меркатора были чисто практическими и основывались на огромных таблицах с данными. При этом он не оставил никаких технических описаний процесса построения карты и соответствующих навигационных таблиц и тем более не создал практического руководства по использованию его карты для навигации. Возможно, по этой причине, а также потому, что мореплаватели считали Меркатора представителем чуждого им мира ученых, эта карта обрела широкую популярность лишь 300 лет спустя. До этого карта Меркатора использовалась считанное число раз: так, друг Меркатора, картограф Абрахам Ортелий, включил в свой атлас «Зрелище шара земного» (Teatrum orbius terrarum, 1570) восемь карт, выполненных в проекции Меркатора.

Математическое описание этой проекции дал кембриджский математик Эдвард Райт (1561–1615). В книге «Ошибки в навигации, обнаруженные и исправленные» (1599, в 1610 году было выпущено дополненное издание) он не только привел новые навигационные таблицы и инструкции по определению фиксированных румбов на картах, составленных в проекции Меркатора, но и объяснил построение подобных карт. Он представлял сферическую модель Земли как полый шар, заключенный внутри цилиндра, касающегося шара на экваторе. Затем в этот шар закачивают воздух так, что он всё больше соприкасается с поверхностью цилиндра. Точки соприкосновения шара и цилиндра являются проекциями точек земной сферы.

Проекция Меркатора распространялась довольно медленно. Голландский картограф Петер Планциус использовал ее в 1594 году при составлении навигационных карт, а Иодокус Хондиус — при построении карты «Изображение всего круга земного» (Typus totus orbis terrarum, 1597) и других. И лишь в 1646–1647 годах в этой проекции Робертом Дадли был создан первый в истории морской атлас.

Карта «Изображение всего шара земного» (Typus totus orbis terrarum, 1597), также известная как «карта рыцаря Христова» Йодокуса Хондиуса, выполненная в проекции Меркатора. В средней части карты вы можете видеть рыцаря Христова, который сражается с Грехом, Сладострастием, Дьяволом и Смертью. Кроме того, Мир подносит ему чашу с ядом вавилонской блудницы, которая иногда использовалась как символ католической церкви.

* * *

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПРОЕКЦИИ МЕРКАТОРА

Чтобы оценить, на каком расстоянии от экватора должны изображаться параллели в проекции Меркатора, будем постепенно увеличивать широту, на которой мы будем применять соответствующий коэффициент масштаба. Если мы начнем отсчет с параллели широтой φ и будем откладывать небольшие интервалы длиной t, получим последовательность точек широтой t, 2t…., φ — t, φ , через которые будут проходить параллели. Так как искажение в направлении меридиана для широты α, как мы уже отмечали, должно равняться искажению вдоль параллели, равному sec φ, то искажение вдоль вертикали в отмеченных нами точках будет равно sec t, sec (2t), sec (φ — t), sec φ. Так как длина дуги сферы, заключенной между отмеченными точками, равна t, то высота, на которой будет проходить параллель широтой φ, будет равна:

t·sect + t·sec(2t) +… + t·sec(φ — t) + t·secφ.

Допустим, мы хотим оценить высоту, на которой будет проходить параллель широтой φ = 60°. Предположим, что выбранные интервалы имеют величину t = 10°. Так как sec 10° = 1,0154, sec 20° = 1,0642, sec 30° = 1,1547, sec 40° = 1,3055, sec 50° = 1,5557 и sec 60° = 2,0000, умножив эти числа на 10 и сложив полученные значения, получим 80,955. Иными словами, параллель широтой 60° должна будет проходить на высоте, на которой располагалась бы параллель широтой 80,955°, если бы параллели были равноудалены друг от друга.

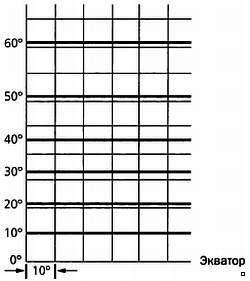
Именно так рассуждал Эдвард Райт, можно предположить, что похожие рассуждения провел и Меркатор. Рассмотрим задачу в более современном виде. Для цилиндрической проекции, 30° в которой экватор является осью х, а параллель широтой φ — горизонтальной линией, проходящей на высоте у = h(φ), коэффициент масштаба (искажения) в направлении меридианов λ должен быть равен коэффициенту масштаба вдоль параллелей μ = 1/cos φ = sec φ. Получим:

Имеем

* * *

Вернемся к проекции Меркатора и напомним, что карта, выполненная в этой проекции, имеет следующие свойства.

1. Она имеет прямоугольную форму, так как выполнена в цилиндрической проекции.

2. Меридианы и параллели пересекаются под прямыми углами.

3. Карта выполнена в конформной проекции, которая не сохраняет расстояния, площади, геодезические линии и формы протяженных участков.

4. Искажения площадей, форм и расстояний вблизи экватора очень малы (в этой части карты используется реальный масштаб), но они значительно возрастают по мере приближения к полюсам, поэтому проекция Меркатора удобна для составления карт территорий, расположенных вблизи экватора.

5. Локсодромы, или линии румба, изображаются в виде прямых линий.

Сравнение локсодромы (линии румба) и ортодромы (линии наименьшего расстояния) между Рио-де-Жанейро и Сеулом на карте Меркатора.

С созданием этой карты мечта Меркатора исполнилась. Если мореплаватель хотел попасть из точки А в точку В, он должен был всего лишь провести на карте, выполненной в проекции Меркатора, прямую, соединяющую эти точки, и измерить румб, соответствующий этой прямой, после чего ему оставалось всего лишь точно соблюдать курс. Однако вы уже знаете, что локсодромы — это не ортодромы, и хотя они указывают простейший курс (нужно всего лишь выдерживать постоянный румб), путь вдоль локсодромы не является кратчайшим. Двигаться вдоль ортодромы сложнее, так как для этого необходимо постоянно менять румб. Мореплаватели и пилоты самолетов в конечном итоге нашли промежуточное решение этой проблемы. Чтобы попасть из пункта отправления в пункт назначения, нужно выполнить следующее.

1. Провести геодезическую линию (прямую) на карте, выполненной в центральной или азимутальной равнопромежуточной проекции с центром в пункте назначения.

2. Разбить геодезическую линию на фрагменты и определить тем самым последовательность стратегических точек.

3. Перенести эти точки на карту, выполненную в проекции Меркатора, и соединить их прямыми. Построенные прямые будут локсодромами и укажут румб, который нужно выдерживать в каждой из стратегических точек.

Метод приближения большого круга с помощью локсодром, который используется в навигации по карте Меркатора, а также, например, карты, выполненной в гномонической проекции.

Нет никаких сомнений в том, что проекция Меркатора была и остается лучшей для составления навигационных карт с момента своего появления в XVII веке. Эту проекцию используют Национальная служба по исследованию океана США (с 1910 года), Гидрографический институт Испании и многие другие авторитетные организации.

Проекция Меркатора играла огромную роль в эпоху морских путешествий. Она очень часто использовалась при составлении карт мира и была одной из самых популярных картографических проекций вплоть до начала XX века, хотя она и вносит очень большие искажения в областях, близких к полюсам. Сегодня на основе этой проекции изготавливаются настенные карты, карты в учебниках и атласах, в научно-популярных публикациях, в газетах и журналах. Американский картограф Джон Снайдер (1926–1997) из Геологической службы США, изучив различные атласы мира, опубликованные в США, Великобритании, Франции и Германии в XIX веке, определил, что чаще всего в них использовалась проекция Меркатора. Однако похожее исследование, проведенное в XX веке, показало, что начиная с 1940-х годов эта проекция практически перестала использоваться. Ей на смену пришли такие проекции, как гомолосинусоидальная проекция Гуда, тройная проекция Винкеля, проекция Робинсона, Eckert IV, проекция Ван дер Гринтена и другие.

* * *

* * *

Поскольку в проекции Меркатора экваториальные зоны изображаются практически без искажений, она очень удобна для составления карт этих областей. Она использовалась в морских картах, составленных лейтенантом американского флота Мэтью Фонтеем Мори (1806–1873). В этих картах содержалась информация о погоде, ветрах, течениях и другие результаты гидрологических и метеорологических наблюдений, а также были указаны морские пути.

Наконец, укажем, что проекция Меркатора используется при построении карт мира в некоторых современных интернет-проектах, в частности «Картах Google» и Virtual Earth. Пользователь этих интерактивных карт может просматривать увеличенное изображение малых областей, которые отображаются практически без искажений. Причина в том, что проекция Меркатора является конформной, то есть на локальном уровне, для небольших областей, вносимые ею искажения невелики.