Примерно две тысячи лет назад для изображения
круглой Земли на плоскости пришлось решить различные математические,
философские и географические задачи, которые привлекли внимание многих
изобретателей.
Разумеется, первые карты появились намного раньше.
Современная картография развивалась медленными
темпами, так как исследование разных уголков Земли началось, по
историческим меркам, сравнительно недавно.
Джон Снайдер «Как Земля стала плоской» (1993)
Картография — это наука, изучающая графическое
изображение Земли и ее частей, а также других небесных тел. В
картографии главным образом рассматриваются карты, а также рельефные
модели и глобусы. В эру компьютеров и интернета карты и глобусы могут
быть очень сложными, интерактивными, созданными с помощью новых способов
изображения земной поверхности.
Карты выполняют две основные функции: они
используются для хранения и представления полезной географической
информации, а также помогают понять пространственные соотношения и
осознать всю сложность мира, в котором мы живем.
Картография делится на три основные части. Первая —
это сбор, анализ и обработка географической информации, которая затем
используется при составлении карт. Источниками географической информации
обычно служат: наблюдения в поле (традиционный источник информации на
протяжении всей истории картографии, применяющийся до сих пор), данные
аэрофотосъемки и космической съемки со спутников (фотографии, данные,
полученные с помощью радаров и датчиков), уже существующие карты и базы
данных, а также статистические данные.
Вторая часть картографии — математическая
картография. Она занимается изучением проекций, то есть геометрических и
математических преобразований, позволяющих изобразить искривленную
земную поверхность на плоскости. Именно проекции определяют, какую форму
будут иметь страны и континенты на картах. Термин «математическая
картография» имеет очень широкое значение. Если говорить коротко, то
математическая картография занимается формированием и изучением
математических основ составления карт, а также охватывает теоретические и
практические вопросы в смежных научных дисциплинах: уже упомянутой
картографии, геодезии, географии, навигации и других науках. Один из
важнейших инструментов математической картографии — дифференциальная
геометрия.
Основной задачей картографии является изучение
проекций. В этой главе мы подробнее расскажем о проекциях, лежащих в
основе карт. Мы приведем их классификацию по форме построения,
геометрическим свойствам, изучим характерные особенности, в частности
искажения, возникающие при использовании разных проекций, а также
рассмотрим основные результаты математической картографии и их
применение при составлении реальных карт.
Третья и последняя часть картографии — это дизайн и
составление карт. Традиционно карты имеют бумажную основу. В прошлом они
рисовались вручную, позднее, с изобретением книгопечатания, стали
изготавливаться печатным способом, и качество карт неуклонно возрастало.
Сегодня благодаря новым технологиям стало возможным публиковать
цифровые карты и карты других форматов. Любой, кто работает с такой
картой, может не просто пассивно получать информацию, но и
взаимодействовать с ней и даже принимать участие в ее создании.
Еще две важные части картографии — это история
картографии, а также изучение способов применения карт. Изучение истории
карт помогает лучше разобраться в них, осознать их роль в истории
человечества и понять, как выглядел мир в разные времена для разных
народов. Не следует забывать, что зная прошлое, мы сможем понять будущее
и сделать его лучше. Наконец, изучение способов применения карт
позволяет сделать их намного эффективнее, создавать новые методы, новые
проекции, которые помогут решить текущие задачи.
Что такое «правильная» карта
В ходе истории картографы и математики работали над
созданием совершенной карты, стремясь найти такую проекцию земной
поверхности на плоскость, которая позволила бы составить наиболее точную
карту нашей планеты. В этой главе мы вновь рассмотрим вопросы,
перечисленные в предисловии. Их можно свести к одному, главному вопросу:
как составить правильную карту Земли? Однако вначале следует выяснить,
какую карту можно считать «правильной».
* * *
КАРТЫ ДЛЯ РАЗГАДКИ ЗАГАДОК
Иногда представление статистических данных на карте
помогает совершить открытие. Карта позволяет увидеть закономерности, не
столь заметные при ином способе представления данных. Простой пример
этого — карта эпидемии холеры, составленная Джоном Сноу в 1854 году. В
середине XIX века причины возникновения холеры и других инфекционных
заболеваний были неизвестны. Возбудителями подобных заболеваний
считались «миазмы» — вредоносные субстанции, передающиеся по воздуху. За
несколько лет Лондон пережил множество вспышек холеры, унесших тысячи
жизней. Английский математик Джон Сноу (1813–1858) считал:
«людей убивает вода». В конце лета 1854 года в районе Сохо разразилась
эпидемия холеры. За первые несколько дней скончалось более 100 человек,
за 10 дней — свыше 500, к концу эпидемии — 616. Сноу, который был
свидетелем эпидемии 1831 года, жил в Сохо. Он заподозрил, что источником
инфекции могла быть колонка с питьевой водой. Жители района брали воду
из уличных колонок, вода в которые поступала из загрязненной Темзы. Сноу
составил карту, на которой отметил местоположение колонок с водой и
дома, где жили жертвы холеры. Он заподозрил, что причиной эпидемии была
колонка на улице Броуд, вокруг которой, как было видно на карте,
проживали заболевшие, которые действительно брали воду именно в этой
колонке. В итоге Сноу удалось добиться закрытия колонки, и лишь спустя
несколько лет было обнаружено, что причиной заболевания являются
бактерии.
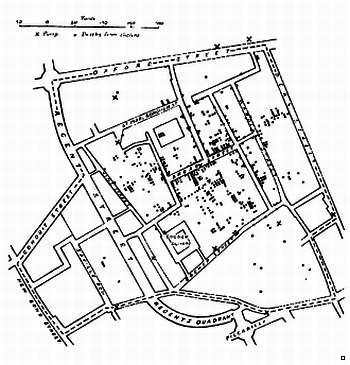 Карта очага эпидемии холеры, составленная Джоном Сноу,
на которой отмечены случаи заболевания холерой в Лондоне в 1854 году.
Точки указывают место жительства заболевших, крестами отмечены колонки с
питьевой водой. Точки сконцентрированы вблизи колонки на улице Броуд.
* * *
Мы можем использовать карты в разных целях: для
поиска кратчайшего пути до точки назначения, определения расстояний,
измерения длин рек, газопроводов или линий связи; для определения зоны
поражения боевой ракеты, области утечки газа или радиационного
заражения. С помощью карт можно определить направление ветра, задать
курс при путешествии в открытом море, на земле или в воздухе, вычислить
площадь определенной территории, проанализировать географическую
информацию, представленную на карте (уровень жизни, плотность населения,
экономические данные или данные об уровне производства товаров и
т. д.). Для решения последней задачи важно, чтобы карта сохраняла
площадь и, если возможно, форму, то есть общий вид рассматриваемых
территорий. Карты позволяют изучать особенности рельефа местности,
например бассейны рек, горные хребты, долины и побережья; при этом очень
важно, чтобы на карте сохранялись их реальные очертания. По сути, при
работе с картой нас интересуют вопросы измерения расстояний, длин
кривых, поиск кратчайших путей (геодезических линий), определение
направлений, углов, площадей и форм. Следовательно, при построении
математических проекций земной поверхности на плоскости мы хотим, чтобы
проекции сохраняли указанные параметры.
Остановимся на мгновение и подумаем о проблеме
составления карты земной поверхности на бытовом уровне, не обращаясь к
методам дифференциальной геометрии, необходимым, чтобы ответить на
вопрос со всей точностью. Несложно увидеть две основные трудности,
возникающие при составлении карт. Одна из них заключается в том, что, в
зависимости от задачи, карты должны иметь разные размеры и на них должны
быть изображены участки земли разной площади. Вторая трудность —
различие между геометрической формой самой Земли и карты, на которой она
изображается: Земля имеет форму сферы, а карта плоская.
Двойная задача: выбор масштаба и картографической проекции
Из всего сказанного следует, что математические
проекции, используемые при составлении карт, становятся понятны, если
рассмотреть построение карт как двухэтапный процесс. Сначала земная
сфера проецируется на сферический глобус, уменьшенный (в масштабе) до
выбранного нами размера. Эта часть проекции заключается в простом
уменьшении изображения земной поверхности. Затем уменьшенное изображение
проецируется на плоскость, в результате чего появляется нужная нам
карта.
* * *
ТОПОЛОГИЧЕСКИЕ КАРТЫ
Если мы нарисуем карту нашего дома, квартала или
района, на ней не будет сохранен ни один из привычных параметров. Точно
такими же были первые карты, созданные человеком, например вавилонская
карта VI века до н. э., изображенная на глиняной табличке. Это так
называемые топологические карты, на которых основное значение имеют
отношения вида «близко — далеко», «вместе — раздельно», а также порядок и
непрерывность. На топологических картах обычно изображают взаимосвязи
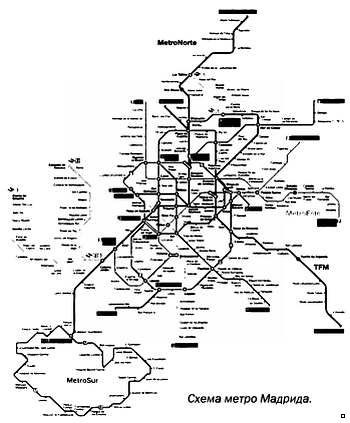
между элементами местности. Хрестоматийным примером таких карт служат
схемы метро, так как для тех, кто ими пользуется, важнее не расстояние
между станциями, а их число и схемы пересадок.
К топологическим картам относятся так называемые
фэнтези-карты вымышленных миров, например карта Средиземья из
«Властелина колец» Дж. Р. Р. Толкиена (1954) или
«живописные карты», которые можно увидеть, например, в парках
аттракционов. К этому же виду относятся карты нейронных сетей и другие
карты, используемые в информатике, а также карты, связанные с графами.
* * *
Описанная выше сферическая модель Земли — это
идеальная модель земной поверхности, которая отличается от нее только
размером, но не формой. Масштаб указывает разницу в размерах между
Землей и сферой. Определить его можно, разделив радиус сферы на радиус
Земли. Рассмотрим глобус радиусом 25 см. Радиус Земли будем считать
равным 6371 км (если использовать размеры эллипсоида WGS84). В этом
случае масштаб равен
Этот масштаб, который обычно записывается как
1:25484000, означает, что каждый сантиметр глобуса соответствует
25484000 см, то есть 254,84 км земной поверхности.
На многих древних картах масштаб указывался с
помощью изображения компаса, как можно видеть на этой карте Магелланова
пролива (1606), выполненной Йодокусом Хондиусом. На карте изображены и другие типичные элементы карт того времени, в частности роза ветров и фантастические животные.
Как влияет это уменьшение в размерах на метрические
параметры карт, о которых мы говорили выше? Расстояния и длины кривых
уменьшаются линейно в соответствии с масштабом, то есть каждый сантиметр
глобуса соответствует 254,84 км земной поверхности. Следовательно, если
мы хотим измерить расстояние от Барселоны до Аделаиды, нужно всего лишь
измерить это расстояние на сферической модели Земли и умножить
результат в сантиметрах на 254,84. Площади участков земной поверхности и
масштаб карты связаны квадратичной зависимостью: каждый квадратный
сантиметр на глобусе будет соответствовать 254,842 = 64943,4256 км2.
Большие круги, указывающие кратчайшие пути, станут
большими кругами на сферической модели, поэтому геодезические линии
также останутся неизменными. Сохранятся также углы и направления. Как
видим, преобразование, которое заключается в уменьшении размеров Земли,
не изменяет метрические параметры, масштаб во всех точках сферической
модели остается постоянным.
Математически это можно выразить следующим образом.
Будем считать, что Земля и ее сферическая модель имеют общий центр,
который мы примем за начало нашего трехмерного пространства 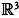 . Следовательно, наше математическое преобразование будет отображением Земли (S1), которая является сферой радиуса 6371 км, на сферическую модель (S2) радиусом 25 см φ: S1 —> S2, определяемым как φ(х) = е·х. На языке геометрии это отображение называется гомотетией (при е > 1 исходные фигуры увеличиваются, при е
< 1, как в нашем случае, — уменьшаются). Это простое преобразование,
которое однозначно определяется свойством пропорционального уменьшения
размеров фигур. . Следовательно, наше математическое преобразование будет отображением Земли (S1), которая является сферой радиуса 6371 км, на сферическую модель (S2) радиусом 25 см φ: S1 —> S2, определяемым как φ(х) = е·х. На языке геометрии это отображение называется гомотетией (при е > 1 исходные фигуры увеличиваются, при е
< 1, как в нашем случае, — уменьшаются). Это простое преобразование,
которое однозначно определяется свойством пропорционального уменьшения
размеров фигур.
Теперь, когда вопрос об изменении размеров решен,
осталось решить проблему изменения формы. Как вы увидите, она намного
сложнее, и именно здесь в действительности скрывается святой Грааль
картографии — идеальная карта. Чтобы решить эту проблему, нужно изучить
математические проекции сферы на плоскость и рассмотреть, как они
изменяют различные метрические свойства. Это центральная тема
математической картографии и настоящей главы. Как мы упоминали в
предисловии, существует множество математических преобразований сферы в
плоскость и, как следствие, множество разных проекций, на основе которых
можно составить столь же большое число самых разных карт. Далее для
простоты мы будем понимать картографические проекции как отображения
сферы единичного радиуса на плоскость  Кроме того, с математической точки зрения проекции должны обладать
некоторыми естественными свойствами: в частности, они должны быть
непрерывными и дифференцируемыми. Это означает, что сфера должна
проецироваться на плоскость разумным образом, то есть без складок,
разрезов и наложений.
Кроме того, с математической точки зрения проекции должны обладать
некоторыми естественными свойствами: в частности, они должны быть
непрерывными и дифференцируемыми. Это означает, что сфера должна
проецироваться на плоскость разумным образом, то есть без складок,
разрезов и наложений.
Как мы уже отмечали, важно знать, как изменяются
основные метрические свойства при использовании тех или иных проекций.
Поэтому начнем наши поиски точной карты земной сферы с того, что докажем
следующее утверждение: в проекции, сохраняющей расстояния между точками
(такие отображения называются изометрическими), также сохраняются
кратчайшие пути (геодезические линии), углы и площади. Кроме того,
сохранение расстояний эквивалентно сохранению длин кривых. Предыдущие
утверждения — не более чем частный случай анализа дифференцируемых
отображений между регулярными поверхностями применительно к их
метрическим свойствам (доказательство этого утверждения методами
дифференциальной геометрии можно найти в любом классическом учебнике по
этой дисциплине).
Проекция, сохраняющая расстояния, сохраняет и кратчайшие пути
Далее мы докажем, что любая проекция сферы на
плоскость, сохраняющая расстояния (это означает, что расстояние между
двумя произвольными точками сферы будет равно расстоянию между
отображениями этих точек на плоскости), также сохраняет кратчайшие пути,
иными словами, отображением больших кругов сферы будут прямые на
плоскости.
Докажем это утверждение методом от противного,
который заключается в том, что мы считаем утверждение, которое хотим
доказать, ложным, и путем логических рассуждений приходим к
противоречию, затрагивающему исходную гипотезу. Следовательно,
утверждение, которое мы хотим доказать, будет истинным. В нашем случае
предположим, что проекцией больших кругов не всегда будет прямая.
Если бы рассматриваемая проекция в самом деле не сохраняла кратчайшие пути, то существовали бы две точки сферы А и В и точка С, лежащая на кратчайшем пути между ними (то есть на большом круге, проходящем через А и В), такая, что ее отображение на плоскость С' не лежало бы на кратчайшем пути (прямой), соединяющем отображения точек А и В — А' и В' соответственно.
Имеем: так как рассматриваемая проекция сохраняет расстояния, то расстояние между отображениями А' и В' равно расстоянию между исходными точками А и В:
d(A, B) = d(A', B').
Так как точка С лежит на кратчайшем пути между А и В, расстояние между этими точками будет равно сумме расстояний между А и С и между С и В:
d(A, B) = d(A, C) + d(C, B).
Тем не менее точка С не лежит на прямой, соединяющей А' и В', следовательно:
d(A', B') < d(A', C') + d(C', B').
Но так как рассматриваемая проекция сохраняет расстояния, то последняя сумма будет равна d(A, С) + d(С, В). Имеем противоречие: мы доказали, что
d(A, B) < d(A, B).
Это очевидно ложное утверждение означает, что проекция не сохраняет кратчайшие пути.
Сохранение расстояний в проекции означает сохранение длин кривых
Используем утверждение из предыдущего раздела
(проекции, сохраняющие расстояния, сохраняют и кратчайшие пути), чтобы
доказать, что в этом случае кривые на сфере преобразуются в кривые на
плоскости, имеющие ту же длину. Почему это утверждение верно? Во-первых,
любую кривую на сфере можно приближенно представить в виде конечного
(но достаточно большого) числа дуг больших кругов. Концы этих дуг р0, р1, р2, …, рn-1, pn лежат на кривой, как показано на иллюстрации.
Следовательно, длину кривой можно приближенно
представить как сумму длин этих дуг, или, иными словами, как сумму
расстояний между их концами. Так как речь идет о дугах больших кругов,
это будут кратчайшие расстояния, соединяющие концы дуг:
l(α) = d(р0, р1) + d(р1, p2) + …+ d(рn-1, рn).
Во-вторых, кривую на плоскости, которая является
отображением исходной кривой на сфере, можно приближенно представить с
помощью множества отрезков, которые будут отображениями дуг больших
кругов (об этом мы рассказали в прошлом разделе), а длину плоской кривой
— как сумму длин расстояний между концами этих отрезков р'0, р'α, р'2, …, p'n :
l(α') = d(р'0, р'1) + d(р'1, p'2) + … + d(р'n-1, р'n).
В-третьих, так как рассматриваемая проекция сохраняет
расстояния, то расстояние между концами отрезков, составляющих исходную
кривую на поверхности сферы, будет равно расстоянию между отображениями
этих точек, которые будут концами отрезков, составляющих проекцию этой
кривой:
d(pi, pi+1) = d(pi, pi+1), i = 0, …, n-1.
Учитывая три приведенных утверждения, можно сказать, что проекция преобразует кривую на сфере в плоскую кривую той же длины.
* * *
СКОЛЬКО КРАСОК НУЖНО, ЧТОБЫ РАСКРАСИТЬ КАРТУ?
Когда мы были детьми, то наверняка рисовали карты,
которые требовалось закрасить так, чтобы области одного цвета не имели
общих границ. Возможно, кто-то даже смог увидеть, что для раскраски
такой карты достаточно четырех красок. Именно эта мысль в середине XIX
века пришла в голову брату одного из студентов Огастеса де Моргана —
Фрэнсису Гутри (позднее он стал математиком и ботаником), когда он
рассматривал карту графств Англии. Де Морган рассказал об этой гипотезе
своим коллегам-математикам.
В 1879 году адвокат сэр Альфред Брей Кемпе, ученик
математика Артура Кэли, предложил доказательство гипотезы о четырех
красках. К сожалению, его доказательство оказалось ошибочным, хотя
содержало интересные и глубокие идеи. Лишь в 1976 году Кеннет Аппель и
Вольфганг Хакен опубликовали окончательное доказательство теоремы о
четырех красках. В нем исходная теорема была выражена на языке теории
графов. Аппель и Хакен пошли от противного и предположили, что исходная
гипотеза ложна и что существуют карты (графы), которые нельзя раскрасить
четырьмя красками, затем они показали, что в таких картах существуют
определенные «неизбежные конфигурации» и, наконец, что все подобные
конфигурации на самом деле можно раскрасить четырьмя красками. Объем
вычислений, которые потребовалось провести на последнем этапе
доказательства, был столь велик, что пришлось прибегнуть к помощи
компьютера, и это вызвало широкую полемику в математическом сообществе.
Можно ли считать доказательство корректным, если оно включает
вычисления, выполненные на компьютере, при этом предполагается, что
любое доказательство должно быть убедительным, формализуемым и, что
самое главное, проверяемым?
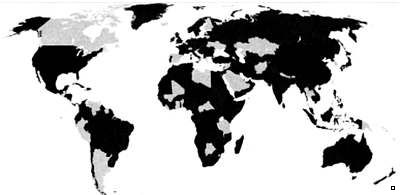 Карта мира, раскрашенная четырьмя красками:
красной, синей, зеленой и желтой (на иллюстрации они представлены
различными оттенками серого). Этих четырех красок достаточно, чтобы
никакие две области, имеющие общую границу, не были окрашены в один
цвет.
* * *
Читатель, знакомый с дифференциальной геометрией или
анализом бесконечно малых, возможно, заметил, что в более строгом
варианте представленного выше доказательства не обойтись без методов
математического анализа.
Утверждение, обратное тому, что мы доказали, также
будет верным: проекции сферы на плоскость, сохраняющие длины кривых,
сохраняют и расстояния между точками. Причина в том, что расстояние
между двумя точками — это длина кратчайшей кривой, их соединяющей.
Проекция, сохраняющая расстояния, сохраняет и углы
Читатель, возможно, понимает, что означает сохранение
величин углов между двумя произвольными направлениями. Но чтобы лучше
понять, как отображения сферы на плоскость изменяют углы, нужно
подробнее рассмотреть используемые понятия, хотя при этом придется
применить некоторые термины.
Рассмотрим произвольную точку сферы р, два направления, проходящие через эту точку, то есть два касательных вектора v1 и v2 а также угол θ
между ними. Чтобы рассчитать, как изменятся касательные векторы и,
следовательно, величина угла, будем действовать следующим образом.
Рассмотрим две кривые на поверхности сферы, α1: (— ε, ε) —> S2 и α2: (— ε, ε) —> S2, которые проходят через точку р. Их касательными векторами в этой точке будут v1 и v2 (если говорить математическим языком, то α'1(0) = v1, α'2(0) = v2 геометрический
смысл этих равенств представлен на следующей иллюстрации). Далее
рассмотрим плоские кривые, которые будут отображениями этих кривых: 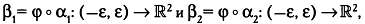 , а также касательные векторы этих кривых в точке пересечения , а также касательные векторы этих кривых в точке пересечения 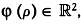 то есть то есть 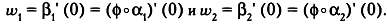
Эти векторы будут отображениями векторов v1 и v2 полученными проекцией φ. Если угол между w1 и w2 вновь будет равен θ, то проекция φ будет сохранять углы между векторами v1 и v2 (а также между кривыми а1 и а2 соответственно). Интересный момент: векторы w1 и w2 которые являются отображениями векторов v1 и v2 полученными проекцией φ, не зависят от исходных кривых а1 и а2 , следовательно, они также не зависят от угла между этими кривыми. Это позволяет, например, выбрать в качестве кривых а1 и а2 дуги больших кругов, проходящие через точку р, и касательные векторы v1 и v2 которые определяются единственным образом.
Следовательно, интуитивно понятно, что изометрические
преобразования сохраняют величины углов. Если для двух больших кругов
сферы, которые пересекаются в точке, мы рассмотрим окружность достаточно
малого радиуса r с центром в этой точке (иными словами, эта
окружность будет образована точками сферы, удаленными от центра
окружности на некоторое расстояние r), то угол θ между
двумя большими кругами (равный углу между их касательными векторами)
будет приблизительно равен отношению длины дуги окружности, определяемой
двумя большими кругами, и ее радиусом, умноженным на 2π.
Далее, если мы рассмотрим отображение, полученное
проекцией, сохраняющей расстояния, то увидим, что проекциями больших
кругов будут прямые (так как изометрические проекции сохраняют
геодезические линии), а окружность радиуса r на сфере перейдет в окружность радиуса r,
центр которой будет располагаться в точке пересечения полученных прямых
на плоскости. Следовательно, так как проекция сохраняет расстояния, а
формула, приведенная на предыдущей иллюстрации, выполняется на
плоскости, угол между большими кругами также будет сохраняться.
Отображения, сохраняющие величины углов, называются
равноугольными, конформными или изогональными. Последний термин напрямую
указывает на то, что проекция сохраняет величины углов неизменными, а
термин «конформный» означает «имеющий одинаковую форму» или «имеющий
правильную форму». Таким образом, проекции, сохраняющие углы, сохраняют и
формы, однако лишь для достаточно малых областей, что можно увидеть на
картах в проекции Меркатора, о которых упоминалось в предисловии. На них
по мере приближения к полюсам искажения становятся очень заметными.
Проекция, сохраняющая расстояния, сохраняет и площади
Это утверждение основано на том, что любую
ограниченную область на поверхности сферы можно покрыть конечным числом
областей, границами которых будут меридианы и параллели. Эти области
можно считать прямоугольными, а их число будет достаточно большим,
следовательно, их размеры невелики. Площадь исходной области можно будет
приближенно выразить как сумму площадей этих «прямоугольников» (их
площадь будет равна произведению основания на высоту). Отображением этой
области будет прямоугольник на плоскости, покрытый множеством
прямоугольников. Так как рассматриваемая проекция сохраняет расстояния,
площадь этого прямоугольника будет равна площади исходной области.
Площадь произвольной территории, например Китая,
можно представить как сумму площадей «прямоугольных» областей,
ограниченных меридианами и параллелями. Чем меньше будут эти области,
тем точнее мы сможем вычислить площадь искомой территории.
Проекции, сохраняющие площади, называются
равновеликими, или гомолографическими. Следовательно, мы доказали, что
отображения сферы на плоскость, сохраняющие расстояния (или длины
кривых), оставляют неизменными площади, геодезические линии и величины
углов — все интересующие нас метрические параметры.
Учитывая вышесказанное, можно сделать вывод: чтобы
построить точную карту мира, нужно найти математическую проекцию сферы
на плоскость, которая была бы изометрической. Приступим же к поискам.
|

