Теперь мы рассмотрим результаты, связанные с треугольниками, кругами и отношениями между площадью и длинами. Эти результаты включают теорему Пифагора, и мы увидим, как она работает в гиперболической геометрии на примере некоторых задач, знакомых нам со школы.

Треугольники

Формула для площади треугольника в евклидовой геометрии всегда одинакова для любого треугольника: s = (b·h/2) то есть площадь равна половине произведения основания треугольника на высоту. В основе этого выражения лежит тот факт, что сумма внутренних углов треугольника всегда равна 180°.

Но в гиперболической геометрии, как ни странно, площадь треугольника зависит от суммы его углов. Как мы уже говорили, в гиперболической геометрии сумма углов треугольника всегда меньше 180°. Следовательно, сумма углов в четырехугольнике также будет меньше 360°.

В евклидовой геометрии если три угла A, В и С одного треугольника и три угла А', В' и С' другого треугольника соответственно равны, то эти треугольники являются подобными. Это не означает, что их соответствующие стороны имеют одинаковую длину. В гиперболической геометрии у таких треугольников с соответственно равными углами будут равны и соответствующие стороны.

Теперь рассмотрим этот случай более подробно. Пусть А, В и С — углы одного треугольника. Их сумма меньше двух прямых углов (180°), и поэтому разность 180 — (А + В + С) будет положительна. Эта разность называется угловым дефектом, и мы имеем следующий результат: площадь любого треугольника пропорциональна его угловому дефекту.

Если мы обозначим через k коэффициент пропорциональности, то формула для площади треугольника (S) будет выглядеть следующим образом:

так что максимальное значение площади треугольника равно π · k² (в гиперболической геометрии не бывает треугольников с бесконечной площадью). Мы не приводим доказательство этого результата, так как оно достаточно сложное. Мы лишь записали окончательную формулу, какой бы странной она ни казалась.

Выражение для площади треугольника подтверждает то, о чем мы говорили раньше. На самом деле в евклидовом случае два треугольника с одинаковыми углами не обязательно имеют одинаковую площадь и, следовательно, не обязательно равны. Однако в гиперболическом мире одинаковые углы (и, следовательно, одинаковый угловой дефект) означают одинаковый размер.

Также в гиперболической геометрии чем больше треугольник, тем больше его площадь и тем меньше сумма его углов. Для очень малых площадей (для бесконечно малых, в терминах математики) сумма углов треугольника стремится к 180°. Таким образом, можно сказать, что геометрия Евклида является предельным случаем гиперболической геометрии.

Иоганн Генрих Ламберт, о котором мы уже упоминали в третьей главе, еще в середине XVIII в. заметил, что, отказавшись от пятого постулата Евклида, он получил следующий результат: сумма углов треугольника увеличилась, приближаясь к 180° по мере уменьшения площади треугольника.

Круги

В школьной геометрии изучаются не только треугольники. В школьную программу входят и другие геометрические фигуры, например, круги, поэтому каждый знает, что такое радиус круга. В геометрии Евклида длина окружности С пропорциональна радиусу r. Это соотношение включает в себя знаменитое число π:

С = 2·π·r.

Однако, в гиперболической геометрии длина окружности рассчитывается по следующей формуле:

В этом выражении k является коэффициентом пропорциональности, a sh — так называемым гиперболическим синусом. Число е нам уже знакомо, с точностью до нескольких десятичных знаков оно записывается как 2,718281828 …Также напомним, что

Теперь возьмем предыдущее выражение

и разложим его в ряд:

Таким образом получим новое выражение для длины окружности в виде бесконечной суммы слагаемых.

Если мы посмотрим на вторую часть выражения

то заметим, что при очень малых r множитель 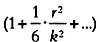будет стремиться к 1, и поэтому формула сведется к известному выражению евклидовой геометрии:

С = 2·π·r.

Это можно доказать с помощью простых вычислений. Для простоты мы будем измерять расстояния в километрах. Возьмем выражение для длины окружности в виде степенного ряда. Пусть коэффициент k имеет значение k = 10¹⁷, и мы хотим посчитать длину окружности радиуса 100 км.

Подставим эти значения в выражение

а также в евклидову формулу 2π·r, и мы увидим, что разница составляет лишь 10^-9.

Если два значения длины окружности посчитать для радиуса в 1 км, разница будет порядка 10^-12. Продолжим вычисления с меньшими значениями по мере того, как круг сжимается. Для радиуса в один метр разница составит примерно 10^-15. Таким образом, мы показали, что при небольших размерах длина окружности в гиперболической геометрии приближается к длине окружности в геометрии Евклида. Такие же рассуждения можно применить и к формулам для площади треугольника.

* * *

РЯДЫ ТЕЙЛОРА

При определенных условиях можно записать следующее разложение в ряд:

Это выражение для е⁴ называется рядом Тейлора, в честь английского математика Брука Тейлора (1685–1713). Если у вас есть простейший калькулятор с четырьмя основными операциями (сложение, вычитание, умножение и деление), эта формула позволяет посчитать е в любой степени, просто подставив его значение вместо А, чем больше членов ряда будет посчитано, тем выше точность результата. Выражение n! означает произведение n·(n — 1)·(n — 2)·…·1 и читается как «n факториал». Например: 5! = 5 x 4 x 3 x 2 x 1 = 120.

Если выражение для ряда Тейлора применить к формуле длины гиперболической окружности

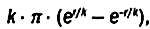
то мы получим:

где последний член очень мал и содержит r в 11-й степени. Если в этом выражении вынести общий множитель С = 2·π·r за скобки, то мы получим следующую формулу:

* * *

Отношение n/k указывает на различие в свойствах фигур в гиперболической и евклидовой геометриях, где п означает размер фигуры (радиус окружности, длина стороны треугольника). Однако в астрономических масштабах отношение n/k нельзя не учитывать.

На самом деле результаты, о которых мы говорили, служат подтверждением того, что гиперболическая геометрия является обобщением евклидовой геометрии. Лобачевский особенно подчеркивал это свойство своей теории, назвав ее пангеометрией, то есть «универсальной геометрией».

Теорема Пифагора

Всегда полезно взглянуть на известные результаты через призму другой теории. Но именно в теореме Пифагора эффект новых геометрий наиболее заметен. В гиперболической геометрии теорема Пифагора играет столь же важную роль, как и в геометрии Евклида, и, как можно было ожидать, для небольших расстояний она ведет себя так же, как и другие гиперболические объекты. Другими словами, на небольших расстояниях она совпадает с евклидовой версией. Однако при увеличении расстояния ситуация меняется.

Рассмотрим гиперболический треугольник, стороны которого мы обозначим а, b и с, где с является гипотенузой; вершинами треугольника будут точки А, В и С. Форма гиперболического треугольника отличается от классической:

Для этого треугольника справедливо равенство

которое может быть переписано в терминах гиперболической геометрии как:

Раскладывая выражение 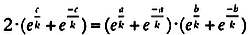в степенной ряд, как мы это делали для формулы длины окружности, мы получим следующее равенство:

Отсюда видно, что в случае небольших сторон треугольника формула Пифагора остается в силе:

с² = а² + Ь²,

принимая традиционный вид, как в евклидовой геометрии.

* * *

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

Гиперболические функции называются так потому, что по свойствам они напоминают классические тригонометрические функции. Они таким же образом связаны с гиперболой, как традиционные тригонометрические функции связаны с окружностью.

* * *

Все эти примеры говорят об общем результате, поэтому мы можем утверждать, что параллельные прямые на гиперболической плоскости в малых областях не отличаются от евклидовых параллельных прямых. С другой стороны, в этих вычислениях использовались гиперболические тригонометрические функции — особые аналоги традиционных функций синуса и косинуса. Они называются гиперболическим синусом и гиперболическим косинусом. Добро пожаловать в гиперболическую тригонометрию.