Для начала мы изложим основные результаты Бойяи и Лобачевского, чтобы лучше понять, как выглядит и работает их геометрия, но мы, конечно, не будем приводить полный перечень всех теорем и доказательств.

Наиболее важным результатом являются изменения в восприятии пространства человеческим разумом. Графические иллюстрации, конечно, играют вспомогательную роль и не являются строгими математическими аргументами, хотя они помогают наглядно пояснить эти понятия.

Как мы уже видели, гиперболическая геометрия является неевклидовой, когда пятый постулат о параллельных прямых заменен следующим: через точку Р вне прямой l можно провести по крайней мере две прямые, параллельные данной. Этот так называемый гиперболический постулат о параллельных прямых может быть проиллюстрирован двумя способами. Оба они эквивалентны и показаны на следующем рисунке:

Из этой гипотезы вытекают различные понятия, лежащие в основе гиперболической геометрии. Мы начнем с основной теоремы.

Углы параллельности

Результат, связанный с углами параллельности, считается основной теоремой гиперболической геометрии. Начнем со следующего рисунка:

Через точку Р вне данной прямой l проходят по крайней мере две прямые, m и n, параллельные l, так что все прямые внутри области I пересекаются с прямой l, а прямые в области II не пересекаются с прямой l. Это означает, что существует бесконечное число прямых, проходящих через точку Р и не пересекающих прямую l. Две крайние параллельные l прямые, тип, разграничивают две области (I и II).

Таким образом, область I ограничена линиями тип, образующими угол (β, который меньше двух прямых углов (180°), как видно на предыдущем рисунке.

Угол β/2 = α называется углом параллельности. Обратите внимание, что α является острым углом (меньшим, чем прямой угол). Это важный факт, так как в евклидовой геометрии такие углы всегда прямые.

На рисунке из точки Р на прямую l опущен перпендикуляр, а расстояние от точки Р до прямой l обозначено буквой d. Мы видим, что угол ОС зависит от длины d (напомним, что мы рассматриваем не плоскую поверхность), так что

1) при уменьшении d α стремится к прямому углу (90°);

2) при увеличении d α стремится к 0.

Этот результат можно наглядно представить с помощью резиновой ленты. Точка Р является концом растянутой резинки, расположенной перпендикулярно прямой l, так что точка Р может двигаться вверх-вниз, увеличивая и уменьшая длину резинки, вместе с которой будут двигаться прямые, проходящие через точку Р. Таким образом, мы увидим, как будет меняться угол параллельности.

При этом существует постоянная величина, которую мы обозначим k, зависящая от единицы измерения длины d и выражаемая следующим образом:

Предыдущий результат можно получить по-другому. Когда значение d увеличивается, правая часть уравнения будет стремиться к 0, и поэтому значение tg (α/2) также стремится к 0, что означает, что α практически 0.

Аналогично, когда d очень мало, значение tg (α/2) — будет приближаться к 1, что означает, что 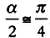, то есть α будет прямым углом, так как π/2 = 90°.

В евклидовой геометрии этот угол не меняется при изменении расстояния. В гиперболической геометрии, как мы видим, угол всегда зависит от величины d.

Эквидистанты

В евклидовой геометрии расстояние между параллельными прямыми на всем их протяжении всегда одно и то же. Как и следовало ожидать, в мире гиперболической геометрии ситуация оказывается несколько иной.

Рассмотрим прямую l и параллельную ей прямую s. Выберем точку Р на s, как на следующем рисунке:

При перемещении точки Р вправо мы видим, что расстояние от Р до прямой l уменьшается. Выражаясь математическим языком, это расстояние стремится к нулю.

Мы также можем сказать, что прямые l и s асимптотически сходятся справа.

Аналогично, если точка Р движется налево, мы видим, что расстояние от Р до прямой l увеличивается. В этом случае говорят, что прямые l и s расходятся. Поэтому, когда в гиперболической геометрии имеются прямые, расстояние между которыми остается постоянным, то такие прямые не могут быть параллельны. Иначе это противоречило бы пятому постулату гиперболической геометрии. Прямая, находящаяся на постоянном расстоянии от данной прямой, называется эквидистантой.