Определить углы, указывающие положение любого астрономического объекта, сравнительно просто. По сути, эта система координат ничем не отличается от той, что используют игроки в морской бой. По-настоящему трудная задача, о которой мы упомянули в начале главы, заключается в определении расстояния до наблюдаемого небесного тела. Существуют особые методы определения расстояний, в которых учитываются физические свойства рассматриваемых объектов. Так как мы говорим о математике в астрономии, мы опишем только один метод, применимый к разным объектам, который часто используется в астрономии и заключается в измерении расстояний при помощи параллакса.

Параллакс — это изменение положения объекта относительно точки отсчета при изменении положения наблюдателя. Это явление знакомо каждому из нас. Делая снимок фотоаппаратом, видоискатель которого расположен на некотором расстоянии от объектива, мы увидим, что изображение не совпадает с тем, что получилось на фотографии. В кадр может не попасть человек, стоящий с краю, или мы можем случайно «обрезать» кому-то ноги. Это происходит потому, что в видоискатель мы видим не совсем то, что попадает в камеру через объектив.

В похожей ситуации оказываются и водители, двигаясь задним ходом: в зависимости от того, куда водитель повернет голову, он увидит дорогу по-разному. Рассмотрим фонарь, стоящий на тротуаре. Если мы посмотрим на него справа, то увидим его, к примеру, в определенном месте на фасаде здания. Если же мы посмотрим на фонарь слева, то увидим, как он сместится в сторону по сравнению с тем, что мы видели раньше.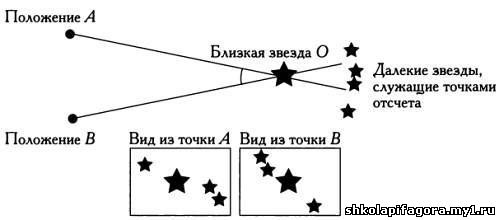

Рассмотрим применение параллакса в астрономии. Как показано на рисунке, положение близкой к нам звезды О меняется в зависимости от того, где располагается наблюдатель. Если мы будем оценивать положение звезды относительно других, достаточно далеких звезд, то увидим, что оно будет изменяться: при наблюдении из точки А будет казаться, что О расположена слева от двух находящихся рядом звезд, при наблюдении из точки В — справа. Угол, под которым виден отрезок АВ из точки О, называется углом параллакса. Величина этого угла обычно очень мала, особенно для объектов, расположенных за пределами Солнечной системы.

Фотографии Луны, сделанные 28 октября 2004 года из Челси, Великобритания (справа), и из Монреаля (Канада). Луна расположена близко к Земле, поэтому при наблюдении из двух точек, отстоящих друг от друга на 5520 км, она будет выглядеть по-разному. Две фотографии были наложены друг на друга так, чтобы изображенные на них звезды совпали.

Если мы будем наблюдать за Луной на фоне звездного неба из двух разных точек земного шара, то сможем вычислить расстояние до нее, зная расстояние между двумя точками, из которых производятся наблюдения. Рассмотрим схему:

Согласно элементарным формулам тригонометрии, имеем:

Следовательно, искомое расстояние будет равно:

В качестве приближенного значения тангенса мы использовали значение самого угла (это соотношение справедливо для малых углов).

Можно определить несколько разновидностей параллакса. Вернемся к предыдущей схеме: если мы будем считать, что точки А и В — это точки, в которых находится Земля, когда она располагается дальше всего от Солнца, получим годовой параллакс. Длина основания треугольника будет равна расстоянию между этими точками, то есть удвоенному расстоянию между Землей и Солнцем — примерно 300 млн километров. 150 млн километров, разделяющие Землю и Солнце, называются астрономической единицей (а. е.). Определив угол параллакса р, получим, что расстояние до звезды (в километрах) равно d = 300 000 000/р, где угол р выражен в радианах.